
14. Лекция № 14
14.1. Сходимость решения нелинейного уравнений установившегося режима.
Рассмотрим простейший из итерационных методов простую итера-
![]()
![]()
![]()
![]()
![]()
 2
r
1
2
r
1
![]()
![]()
а)
![]()
 М
М
![]()
![]()
0
![]()
![]()
![]()
![]()
![]() x
x
б)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
М
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
в) г)
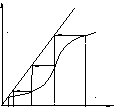
Рис. 14.1 Теометрическая интерпретация простой итерации:
а – схема замещения линии с активным сопротивлением; б, в – сходимость и расходимость простой итерации; г – колебательная сходимость простой итерации.
итерацию на примере решения нелинейного уравнения напряжений для нагрузочного узла 2 линии с активным сопротивлением (рис.14.1,а):
![]() (14.1)
(14.1)
где
![]() - собственная
проводимость узла 2;
- собственная
проводимость узла 2;
![]() - напряжения
узлов 1 и
2 линии;
- напряжения
узлов 1 и
2 линии;
Р2 - мощность нагрузки в узле 2 (которая не равна мощности в узле 1).
Мощность Р2,
проводимость
![]() и напряжение
и напряжение
![]() заданы. В
результате решения уравнения (14.1)
надо найти зависимую переменную
заданы. В
результате решения уравнения (14.1)
надо найти зависимую переменную
![]() .
Запишем уравнение (14.1) в виде:
.
Запишем уравнение (14.1) в виде:
![]() .
(14.2)
.
(14.2)
Зададимся начальным
приближением
![]() и подставим
его в правую часть уравнения (14.2). Новое
приближение напряжения узла 2;
и подставим
его в правую часть уравнения (14.2). Новое
приближение напряжения узла 2;
![]() .
(14.3)
.
(14.3)
Подставив теперь
в правую часть уравнения (14.3) вместо
![]() значение
значение
![]() получим следующее приближение напряжения:
получим следующее приближение напряжения:
![]() .
(14.4)
.
(14.4)
Повторяя этот процесс, получим итерационную последовательность:
![]() (14.4)
(14.4)
Обозначим в общем виде через х - зависимую переменную, определяемую в результате решения уравнения установившегося режима. Тогда:
![]() (14.4)
(14.4)
Возьмем начальное
приближение
![]() и будем строить
последовательность чисел
и будем строить
последовательность чисел
![]() ,
определенных
с помощью итерационного метода:
,
определенных
с помощью итерационного метода:
![]() (14.7)
(14.7)
Для того чтобы пояснить причины сходимости или расходимости метода, приведем геометрическую интерпретацию простой итерации.
На рис. 14.1,б приведены
кривая
![]() и прямая
и прямая
![]() .
Решение
.
Решение
![]() уравнения
(14.6) - это абсцисса точки пересечения М
кривой и прямой.
Двигаясь от точки
уравнения
(14.6) - это абсцисса точки пересечения М
кривой и прямой.
Двигаясь от точки
![]() с координатами
с координатами
![]() ,
построим ломаную линию
,
построим ломаную линию
![]() …
Отрезки ломаной линии попеременно
параллельны осям Ох,
О.
Точки
…
Отрезки ломаной линии попеременно
параллельны осям Ох,
О.
Точки
![]() ...
лежат на кривой
...
лежат на кривой
![]() ,
а точки
,
а точки
![]() ...
- на прямой
...
- на прямой
![]() .
Последовательные приближения неизвестной
х равны
.
Последовательные приближения неизвестной
х равны
![]() ...
На рис.14.1,б кривая
...
На рис.14.1,б кривая
![]() в окрестности решений
в окрестности решений
![]() пологая, то есть
пологая, то есть
![]() ,
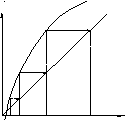
и процесс итерации сходится. Если
,
и процесс итерации сходится. Если
![]() ,
то процесс итерации будет расходиться
(рис.14.1,в). В этом случае как бы ни было
близко начальное приближение, итерационный
процесс не сходится к решению [3].
,
то процесс итерации будет расходиться
(рис.14.1,в). В этом случае как бы ни было
близко начальное приближение, итерационный
процесс не сходится к решению [3].
Из рис.14.1, б, в
видно, что
сходимость метода простой итерации
определяется значением производной
![]() .
Более того,
знак этой производной определяет
характер итерационного процесса -
монотонный или колебательный. При
монотонной сходимости все поправки
.
Более того,
знак этой производной определяет
характер итерационного процесса -
монотонный или колебательный. При
монотонной сходимости все поправки
![]() одного знака,
при колебательной знаки
одного знака,
при колебательной знаки
![]() различны. Если в точке решения
различны. Если в точке решения
![]() и
и
![]() ,
то итерационный процесс
монотонно сходится к решению. При
,
то итерационный процесс
монотонно сходится к решению. При
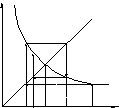
![]() сходимость колебательная. Пример
колебательного итерационного процесса
приведен на рис.14.1, г. При монотонном
итерационном процессе на рис.14.1, б
все приближения
находятся справа от решения, то есть
все
сходимость колебательная. Пример
колебательного итерационного процесса
приведен на рис.14.1, г. При монотонном
итерационном процессе на рис.14.1, б
все приближения
находятся справа от решения, то есть
все
![]() больше, чем
решение
больше, чем
решение
![]() .
Итерационный процесс идет по спирали,
колебательно приближаясь к решению.
Отметим, что
расходящийся итерационный процесс
может быть как монотонным (рис. 14.1, в),
так и колебательным.
.
Итерационный процесс идет по спирали,
колебательно приближаясь к решению.
Отметим, что
расходящийся итерационный процесс
может быть как монотонным (рис. 14.1, в),
так и колебательным.
Для сходимости методов простой итерации и Зейделя необходимо и достаточно, чтобы все собственные значения матриц В или 3 были по модулю меньше единицы. Это значит, что должно выполняться условие:
![]() (14.8)
(14.8)
где
![]() - наибольшее
по модулю собственное значение матрицы
В
или 3.
Отыскание всех собственных значении
матрицы В
или 3представляет
собой задачу более сложную, чем решение
системы линейных алгебраических
уравнений, и поэтому неэффективно для
проверки сходимости.
- наибольшее
по модулю собственное значение матрицы
В
или 3.
Отыскание всех собственных значении
матрицы В
или 3представляет
собой задачу более сложную, чем решение
системы линейных алгебраических
уравнений, и поэтому неэффективно для
проверки сходимости.
При анализе сходимости решения систем линейных алгебраических уравнений используются три легко вычисляемые нормы матрицы В (или 3): m-норма матрицы равна наибольшей из сумм абсолютных величин элементов одной строки матрицы; l-норма равна наибольшей из сумм абсолютных величин элементов одного столбца матрицы; k-норма равна корню из суммы квадратов элементов матрицы [3]. Для сходимости процессов простои итерации и Зейделя при решении систем линейных уравнений при любом начальном приближении достаточно, чтобы любая из указанных норм матрицы была меньше единицы. Несоблюдение любого из достаточных условий еще не значит, что итерационный процесс расходится. Выполнение же любого из этих условий означает, что методы простой итерации и Зейделя сходятся.
Для линейных уравнений узловых напряжений достаточные условия сходимости методов простой итерации и Зейделя не выполняются. Поэтому с помощью достаточных условий нельзя проверить сходимость решения этих уравнении.
Метод по параметру необходимо использовать в расчете установившегося режима в тех случаях, когда расходится метод Ньютона. Ряд модификаций метода по параметру определяется следующей итерационной формулой:
![]() (14.9)
(14.9)
где
![]() - обратная матрица Якоби при
- обратная матрица Якоби при
![]() ;
;
![]() - вектор-функция
небалансов мощности в узлах при
- вектор-функция
небалансов мощности в узлах при
![]() ;
;
![]() - векторы переменных
на i-м
и (I+l)-м
шагах итерационного процесса;
- векторы переменных
на i-м
и (I+l)-м
шагах итерационного процесса;
t
- параметр, причем
![]()
![]() .
.
При t=1
итерационный процесс (14.9)
совпадает с методом Ньютона. Процесс
(14.9) соответствует
умножению, поправок
![]() ,
определяемых при решении системы
линейных уравнении в методе Ньютона,
на параметр t.
В этом смысле методы по параметру можно
рассматривать как «ускоренные» методы
Ньютона и параметр t
аналогичен коэффициенту ускорения.
,
определяемых при решении системы
линейных уравнении в методе Ньютона,
на параметр t.
В этом смысле методы по параметру можно
рассматривать как «ускоренные» методы
Ньютона и параметр t
аналогичен коэффициенту ускорения.
