11.2. Применение метода Гаусса и матрицы для решения уравнений узловых напряжений.

Метод Гаусса при расчете нелинейных уравнений узловых напряжений можно использовать на каждом шаге итерационного процесса, считая систему нелинейных уравнений узловых напряжений линейной на данном шаге.[3] 3дадимся начальными приближениями узловых напряжений, т. е. зададимся начальным приближением вектора-столбца переменных . Определим правые части в нелинейной системе уравнений узловых напряжений в форме баланса токов (11,1) или (11.2), т. е. вычислим элементы вектор-столбца при :

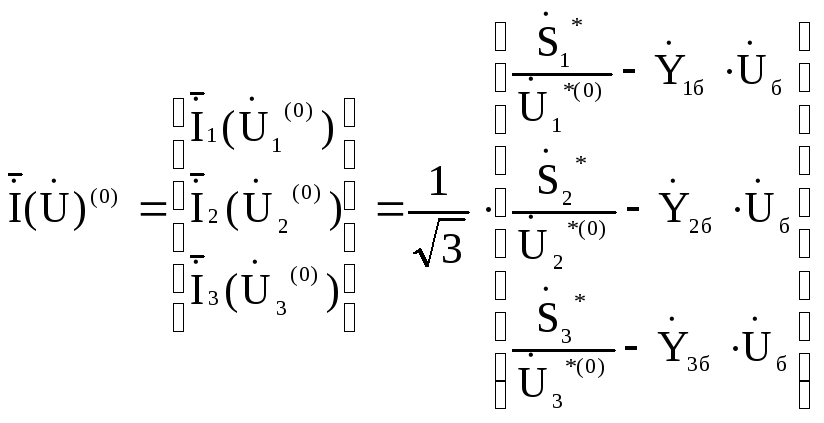. (11.9)

Токи в узлах постоянны и определяются начальными приближениями узловых напряжений. Тогда уравнения узловых напряжений (11.3) превращаются в систему линейных алгебраических уравнений с правыми частями, вычисляемыми из (11.9):

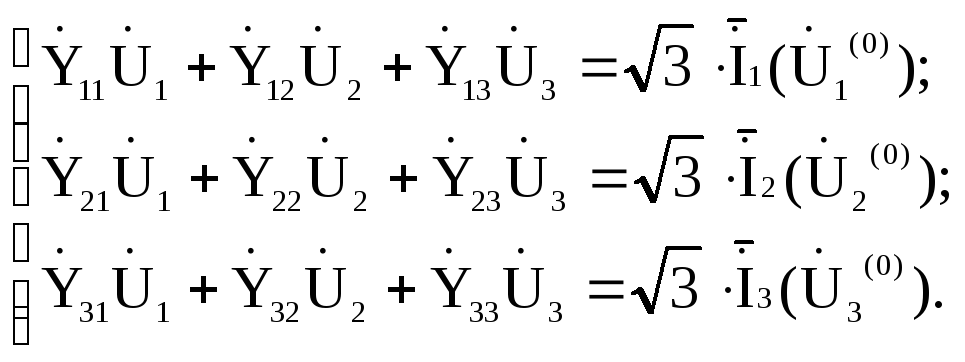(11.10)

В матричной форме линейную систему (11.10) можно записать следующим образом:

. (11.11)

Решая систему (11,11) определяем первое приближение напряжений узлов Далее переходим, ко второму шагу, то есть определяем правые части (11.3) при значениях узловых напряжений, равных их первым приближениям:

. (11.12)

Затем найдем второе приближение узловых напряжений, решая линейную систему с той же матрицей и так далее до тех пор, пока процесс не сойдется:

. (11.13)

, (11.14)

где i – номер шага.

Для решения линейной системы уравнений узловых напряжений (11.14) на каждом шаге итерационного процесса целесообразно использовать метод исключения по Гауссу. В этом случае система комплексных уравнений заменяется на действительную, аналогичную (11.14). Для эффективного решения линейных уравнений установившегося режима по Гауссу необходимо учитывать слабую заполненность матрицы узловых проводимостей.

Матрица может использоваться для решения на каждом шаге итерационного процесса линейных алгебраических уравнений (11.4). Напомним, что матрица собственных и взаимных сопротивлений узлов обратная по отношению к матрице узловых проводимостей, то есть:

. (11.15)

На каждом шаге итерационного процесса узловые напряжения определяются по выражению:

, (11.16)

где - вектор-столбец, каждый элемент которого равен напряжению балансирующего узла;

-вектор-столбец задающих токов, определяемых на (I+1)-м приближении узловых напряжений, при этом k-й элемент вектор-столбца равен

Основное достоинство расчета установившегося режима с помощью узловых сопротивлений это быстрая сходимость. Однако существенным недостатком этого метода является необходимость определять и, главное, запоминать матрицу , в которой нет нулевых элементов.

Расчет установившегося режима с помощью собственных и взаимных сопротивлений может оказаться эффективным в тех случаях, когда он проводится для одной и той же системы очень большое количество раз. Кроме того, применение матрицы эффективно для расчетов установившихся режимов электрических систем - с тяговой нагрузкой, а также в расчетах токов короткого замыкания.

Основное преимущество применения на каждом шаге итерационного процесса метода Гаусса перед использованием обратной матрицы состоит в повышении эффективности расчета за счет учета слабой заполненности матрицы . Поэтому применение этого итерационного процесса предпочтительнее использования матрицы .

Решение на каждом шаге линейной системы уравнений узловых напряжений по методу Гаусса не нашло применения в расчетах установившихся режимов, поскольку такой способ не имеет никаких преимуществ по сравнению с расчетом установившегося режима по методу Ньютона.