9.5. Метод Гаусса

Методы решения линейных уравнений установившегося режима можно разделить на две группы: точные (или прямые) и итерационные (или приближенные) [3].

Точными или прямыми методами называются такие, которые в предположении, что все вычисления ведутся точно (без округлений), позволяют получить точные значения неизвестных в результате конечного числа операций. Практически все вычисления ведутся с округлениями, поэтому и значения неизвестных, полученных точным методом, будут содержать погрешности. Из точных методов ниже рассмотрим метод Гаусса.

Итерационными (приближенными) методами называют такие, которые даже в предположении, что вычисления ведутся без округлений, позволяют получить решение системы уравнений лишь с заданной точностью. Точное решение системы в случае применения итерационных методов может быть получено теоретически как результат бесконечного итерационного процесса. Рассмотрим два итерационных метода: простую итерацию и метод Зейделя. Эти методы не всегда сходятся при решении линейных уравнений установившегося режима.

Метод последовательного исключения (метод Гаусса) - один из наиболее распространенных способов решения систем линейных алгебраических уравнений [3]. Если точно выполнить все действия метода Гаусса, то получим точное решение системы. Алгоритмы, с помощью которых может быть реализован метод Гаусса, различны.

Рассмотрим один из них - алгоритм единственного деления (или алгоритм с обратным ходом). Запишем систему трех уравнений узловых напряжений (9.1) в следующем виде:

. (9.24)

Пусть (ведущий элемент) либо в противном случае переставим уравнения так, чтобы это условие выполнялось. Разделим первое уравнение системы (9.24) на и получим

, (9.25)

где (j = 2, 3) .

Теперь, пользуясь уравнением (9.25), можно исключить неизвестное из второго и третьего уравнений системы (9.24). Для этого исключения нужно умножить уравнение (9.25) на и и вычесть результаты соответственно из второго и третьего уравнений системы (9.24). В результате получим систему двух уравнений с двумя неизвестными:

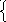, (9.26)

где коэффициенты , вычисляют по формулам:

(k, j = 2, 3); . (9.27)

Из системы (9.26) можно также исключить переменную , как исключили из системы (9.24). Для этого разделим коэффициенты первого уравнения системы на ведущий элемент и получим:

, (9.28)

где ; .

Затем умножим (9.22) на и вычтем результат из второго уравнения системы (9.26). При этом получим уравнение

или , (9.29)

где

, . (9.30)

Таким образом, система (9.24) приведена к эквивалентной схеме с треугольной матрицей:

. (9.31)

Из системы (9.31) последовательно найдем значения всех трех неизвестных:

. (9.32)

Решение по методу Гаусса распадается на два этапа:

- прямой ход - приведение системы (9.24) к эквивалентной системе (9.31) с треугольной матрицей;

- обратный ход - вычисление неизвестных в соответствии с (9.32).

При расчете установившегося режима матрица узловых проводимостей симметричная. Соответственно матрицы систем, вычисляемые при реализации метода Гаусса, также симметричные.

Это обстоятельство можно использовать для экономии памяти. Кроме того, вследствие симметричности элементов матрицы количество арифметических операций может быть сокращено почти вдвое при реализации тех вариантов метода Гаусса, когда ведущие элементы выбираются на диагонали.

При расчете режима сети переменного тока по методу Гаусса на ЭВМ система комплексных уравнений, как правило, заменяется эквивалентной системой действительных переменных порядка 2n, где (n + 1) - число узлов в системе (9.12).

Достоинство метода Гаусса состоит в том, что при его применении гарантируется получение решения в результате выполнения определенного числа арифметических операций, причем число необходимых операций определяется только порядком системы п. В этом состоит преимущество метода Гаусса и других точных методов перед приближенными, или итерационными. Для последних число необходимых арифметических вычислений зависит не только от порядка системы, но и от заранее неизвестного количества шагов, за которое сойдется итерационный процесс.

Недостаток метода Гаусса состоит в необходимости пересчитывать матрицу коэффициентов системы уравнений, Для расчета сложных электрических систем эффективное применение метода Гаусса невозможно без использования специальных методов, учитывающих слабую заполненность матрицы узловых проводимостей.