
Среднее Заочное отделение / 4 семестр / Цифровые и микропроцессорные устройства / Электронный конспект лекций (ЦиМПУ)
.pdfтоматах без памяти) каждый символ на выходе определяется комбинацией символов на входах в текущий момент времени и не зависит от того, какие символы ранее действовали на этих входах, т. е. КЦУ не обладают памятью. В ПЦУ (цифровых автоматах с памятью) выходной сигнал определяется набором символов на входах в текущий момент времени и внутренним состоянием устройства, которое зависит от предыдущих значений символов на входах, т. е. ПЦУ обладают памятью.
1.2.3 Способы задания логических функций
Для задания логических функций используют два способа: табличный и аналитический.
При табличном способе строится таблица истинности, в которой приво-
дятся все возможные значения наборов аргументов и значения логической функции, которые она принимает на каждом наборе. Число наборов аргументов
N, т. е. число строк в таблице истинности, определяется по формуле |
N |
|
n – число аргументов. Например, таблица истинности для логических одного аргумента приведена в таблице 1.5. Существует всего четыре одного аргумента.
2 |
n |
, |
|
||
|
|
где |
функций
функции
Таблица 1.5 – Таблица истинности для элементарных логических функций одного аргумента
Аргумент X |
|
|
Логические функции |
|
|
||||
|
|
|
|
|
|
|
|
|
|
f |
(X) |
|
f |
(X) |
f |
(X) |
f |
(X) |
|
|
|
||||||||
|
0 |
|
|
1 |
|
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
0 |
|
1 |
|
1 |
1 |
|
0 |
|
|
1 |
|
0 |
|
1 |
При n = 2 число наборов значений аргументов равно 22 4, а число функ-
ций – |
2 |
4 |
16. |
Таблица истинности для логических функций двух аргументов |
|
||||
|
|
|
представлена в таблице 1.6.
Таблица истинности наиболее наглядно описывает функционирование некоторого логического устройства, но, чтобы построить логическую схему устройства, необходимо логическую функцию задать аналитическим способом.
При аналитическом способе логическая функция записывается в форме логического выражения, показывающего, какие логические операции над аргументами функции и в какой последовательности должны выполняться.
31
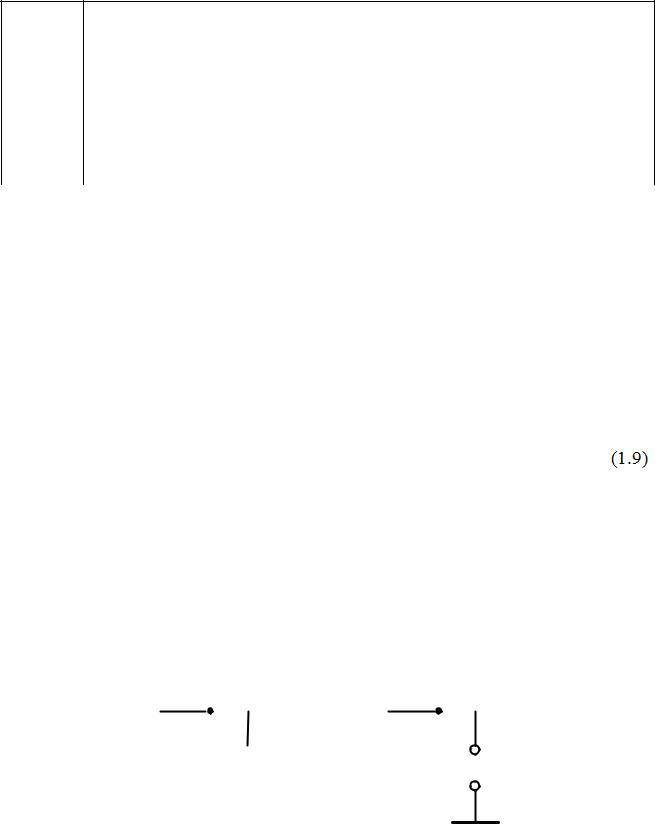
Таблица 1.6 – Таблица истинности для элементарных логических функций двух аргументов
Аргу- |
Функции |
|
менты |
||
|
X |
X |
2 |
f |
0 |
f |
f |
2 |
f |
3 |
f |
4 |
f |
5 |
f |
6 |
f |
7 |
f |
8 |
f |
9 |
f |
f |
f |
f |
f |
f |
1 |
|
|
1 |
|
|
|
|
|
|
|
|
10 |
11 |
12 |
13 |
14 |
15 |
||||||||||
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|||||||||
0 |
1 |
|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|||||||||
1 |
0 |
|
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
|||||||||
1 |
1 |
|
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
|||||||||
1.2.4 Элементарные логические функции одного аргумента
Как отмечалось выше, для одного аргумента можно составить четыре элементарные логические функции. Логические функции одного аргумента (таблица 1.5) представляются следующими выражениями:
f0 (X) 0 (константа 0); |
|
||
f1(X) X (повторение); |
|
||
|
|||
|
|
|
|
|
|
|
|
f2 (X) X (логическая операция НЕ); |
|||
f3 (X) 1 (константа 1). |
|
||
|
|||
Логический элемент, реализующий функцию |
f |
0 |
(X), |
называется генерато- |
||||
|
|
|||||||
ром нуля. Для формирования функции |
f |
0 |
(X) |
выход логического элемента под- |
||||
|
|
|||||||
ключается к общей точке схемы, т. е. к корпусу устройства (рисунок 1.4, а).
X
f |
0 |
(X) 0 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X
f |
3 |
(X) 1 |
||
|
|
|
||
|
|
|
|
|
+
Uп
а) |
б) |
Рисунок 1.4 – Реализация элементарных логических функций одного аргумента f0 (а) и f3 (б)
32
Логический элемент, реализующий функцию |
f |
3 |
(X), |
называется генерато- |
|||
|
|
||||||
ром единицы. Для формирования функции |
f |
3 |
(X) |
выход логического элемента |
|||
|
|
||||||
подключается к источнику питания, соответствующего логической единице (рисунок 1.4, б).
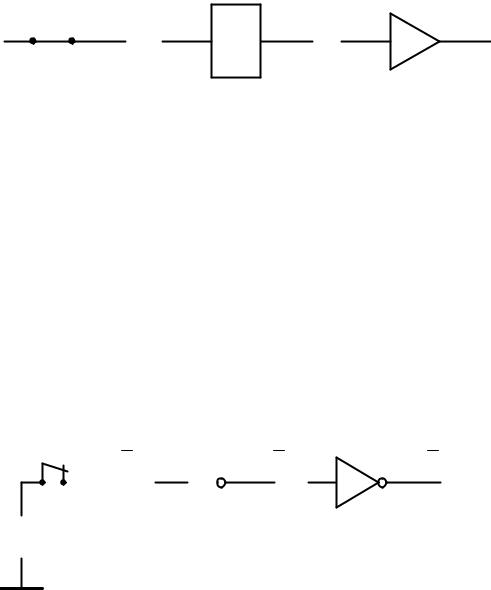
Логический элемент, реализующий функцию f1(X) называется повторителем. Для формирования функции f1(X) выход логического элемента соединяется со входом (рисунок 1.5, а). Условное графическое обозначение (УГО) повторителя по ГОСТ 2.743-91 ЕСКД и вариант по стандарту ANSI (от англ. American National Standards Institute) представлены на рисунке 1.5, б и 1.5, в соответ-
ственно.
X |
f |
1 |
(X) = X |
X |
1 |
f |
1 |
(X) |
X |
f |
1 |
(X) |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
а) |
|
|
б) |
|
|
|
|
в) |
|
|
|
Рисунок 1.5 – Реализация элементарной логической функции |
f |
1 |
обозначение повторителя (б и в)
(а) и условное графическое
Повторители в цифровой схемотехнике используются для усиления сигнала по мощности, т. е. для увеличения нагрузочной способности логических элементов.
Логический элемент, реализующий функцию |
f |
2 |
(X), |
называется инвертором, |
||||
|
|
|||||||
либо логическим элементом НЕ. Для формирования функции |
f |
2 |
(X) |
выход логиче- |
||||
|
|
|||||||
ского элемента соединяется со входом через нормально замкнутый контакт электромеханического переключателя, например реле (рисунок 1.6, а).
X = 0
f |
(X) X |
|
2 |
|
|
|
|
|
 + Uп
+ Uп
X 1
0
1
f |
(X) X |
2 |
|
1
0
X
f |
(X) X |
2 |
|
а) |
б) |
в) |
Рисунок 1.6 – Реализация элементарной логической функции f2(x) (а) и условное графическое обозначение инвертора (б и в)
33

УГО инвертора по ГОСТ 2.743-91 ЕСКД и вариант по стандарту ANSI представлены на рисунке 1.6, б и 1.6, в соответственно.
1.2.5 Элементарные логические функции двух аргументов
Известно, что логические функции могут быть многоаргументными. На основе законов алгебры логики все они могут быть выражены через функции с числом аргументов не более двух. Все логические функции с числом аргументов не более двух являются элементарными, так как содержат только одну логическую операцию.
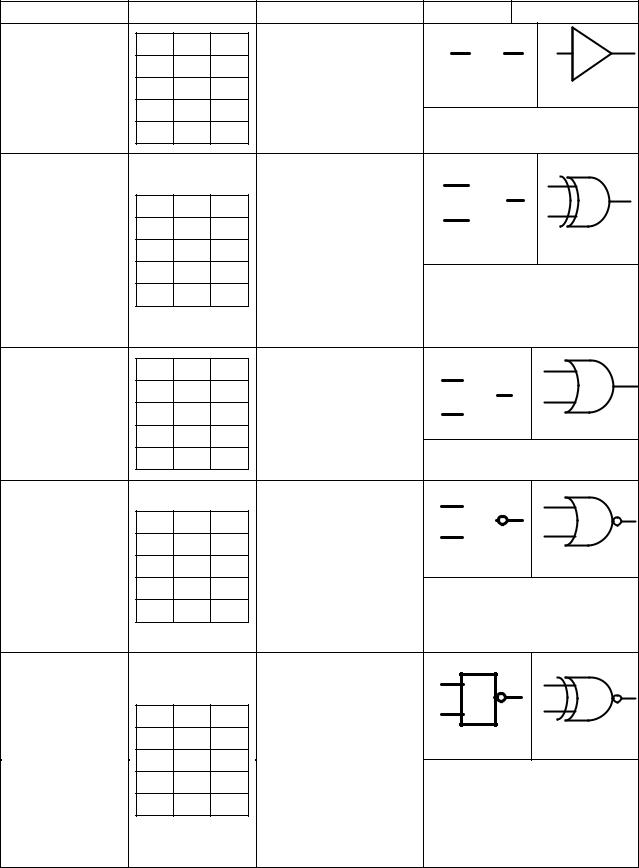
Рассмотрим все возможные функции двух аргументов. Для этого из таблицы 1.6 запишем в таблицу 1.7 их значения истинности, а также рассмотрим их запись, наименование, а также УГО и название соответствующих логических элементов.
Из рассмотренных в таблице 1.7 функций не представляют практического интереса: f2, f4 (запрет) и f11, f13 (импликация).
1.2.6 Основные законы и тождества алгебры логики
Логические функции могут быть представлены в различных формах. Эквивалентные преобразования логических функций из одной формы в другую основаны на законах и тождествах алгебры логики. К ним относятся:
– Свойства конъюнкции, дизъюнкции и инверсии:
X · X = X, X · 1 = X, X · 0 = 0, X · X = 0; |
(1.10) |
||||||
X ˅ X = X, X ˅ 1 = 1, X ˅ 0 = X, X ˅ X =1; |
(1.11) |
||||||
X = X, X = X, если X |
1 |
= X |
, то X |
1 |
= X |
. |
(1.12) |
|
2 |
|
2 |
|
|
||
Справедливость этих выражений может быть доказана с помощью таблиц истинности.
Второе свойство инверсии ̿ называется законом двойного отрица-
ния.
34

Таблица 1.7 – Полная совокупность элементарных логических функций двух аргументов
|
|
|
|
|
|
|
Условное графическое |
|||||||||
|
|
|
|
Запись функции в |
|
|
|
обозначение и |
|
|
||||||
Номер и |
Таблица |
основном базисе |
|
|
|
наименование |
|
|
||||||||
наименование |
(с помощью |
логического элемента |
|
|||||||||||||
истинности |
|
|||||||||||||||
функции |
самостоятель- |
по ГОСТ |
|
|
|
|
|
|||||||||
|
|
|
по стандарту |
|||||||||||||
|
|
|
|
ной нотации) |
2.743-91 |
|||||||||||
|
|
|
|
|
|
ANSI |
|
|
||||||||
|
|
|
|
|
|
|
ЕСКД |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1 |
|
2 |
|
|
3 |
|
|
|
|
4 |
|
|
|
5 |
|
|
Функция f0. |
x1 |
x2 |
f0 |
|
|
|
|
|
|
G |
f0 |
|
|
|
|
|
0 |
0 |
0 |
f0 = 0 |
|
|
|
|
0 |
|
|
|
|
|
|
||
Константа |
|
|
|
|
|
|
|
|
|
|
||||||
0 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
__ |
|
|
|
|
|
|
|
|
|
|
||||
нуль |
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
0 |
0 |
(f0 = 0 = f15) |
|
|
|
|
|
|
|
|
|
|
|||
(функция 0) |
|
|
|
|
|
|
|
|
|
|
||||||
1 |
1 |
0 |
|
|
|
|
|
|
Генератор нуля |
|
|
|||||
|
|
|
|
|
|
|
|
|
||||||||
|
x1 |
x2 |
f1 |
|
|
|
X |
1 |
& |
f1 |
X |
1 |
f1 |
|||
|
|
|
|
|
|
|
||||||||||
Функция f1. |
|
|
|
|
|
|
|
|
|
|||||||
0 |
0 |
0 |
f1 = X1 |
X2 |
X2 |
|
|
X2 |
|
|
||||||
Конъюнкция |
|
|
|
|
|
|
|
|
|
|
||||||
0 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
__ |
|
|
|
|
|
|
|
|
|
|
||||
(логическая |
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
0 |
0 |
(f1 = X1 ∙ X2 = f14) |
|
|
|
|
|
|
|
|
|
|
|||
операция И) |
|
|
|
|
|
|
|
|
|
|
||||||
1 |
1 |
1 |
|
|
|
|
|
Конъюнктор (ЛЭ И) |
|
|||||||
|
|
|
|
|
|
|
||||||||||
Функция f2. |
|
|
|
|
|
|
X |
|
|
|
X |
1 |
f |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Запрет |
x1 |
x2 |
f2 |
|
|
|
1 |
& |
f2 |
|
|
|
2 |
|||
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
первого |
0 |
0 |
0 |
|
|
|
X |
|
|
|
|
2 |
|
|
||
f2 = X1 |
̅̅̅ |
2 |
|
|
|
|
|
|
|
|||||||
аргумента |
0 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
(логическая |
1 |
0 |
1 |
(f2= X1 |
X2 = ̅̅̅̅) |
|
Элемент запрета (ЛЭ |
|
||||||||
операция |
1 |
1 |
0 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
НЕТ) |
|
|
|||||||
НЕТ) |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Функция f3. |
x1 |
x2 |
f3 |
|
|
|
X1 |
1 |
f3 |
X |
1 |
f3 |
|
|||
Повторение |
|
|
|
|
|
|
||||||||||
0 |
0 |
0 |
f3 = X1 |
|
|
|
|
|
|
|
|
|
|
|||
первого |
|
|
|
|
|
|
|
|
|
|
||||||
0 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
__ |
|
|
|
|
|
|
|
|
|
|
||||
аргумента |
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
0 |
1 |
(f3 = X1 = f12) |
|
|
|
|
|
|
|
|
|
|
|||
(логическая |
|
|
|
|
|
|
|
|
|
|
||||||
1 |
1 |
1 |
|
|
|
|
|
|
Повторитель |
|
|
|||||
операция ДА) |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Функция f4. |
|
|
|
|
|
|
X |
|
|
|
|
X1 |
|
f4 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Запрет |
x1 |
x2 |
f4 |
|
|
|
|
|
1 |
& |
f4 |
|
|
X2 |
|
|
|
___ |
|
|
|
|
|
|
|
|
|||||||
второго |
0 |
0 |
0 |
|
|
X |
|
|
|
|
|
|
|
|||
|
|
2 |
|
|
|
|
|
|
|
|||||||
f4 = X1 · X2 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||||||||
аргумента |
0 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
__ |
|
|
|
|
|
|
|
|
|
|
||||
(логическая |
1 |
0 |
0 |
(f4 = X2 |
X1 = f11) |
|
Элемент запрета (ЛЭ |
|
||||||||
операция |
1 |
1 |
0 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
НЕТ) |
|
|
|||||||
НЕТ) |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
35 |
Продолжение таблицы 1.7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
Функция f5. |
x1 |
x2 |
f5 |
|
|
X2 |
1 f5 |
|
X2 |
f5 |
|||
Повторение |
|
|
|
||||||||||
0 |
0 |
|
0 |
f5 = X2 |
|
|
|
|
|
|
|
||
второго |
|
|
|
|
|
|
|
|
|||||
0 |
1 |
|
1 |
|
|
|
|
|
|
|
|||
|
|
__ |
|
|
|
|
|
|
|
||||
аргумента |
|
|
|
|
|
|
|
|
|
||||
1 |
0 |
|
0 |
(f5 = X2 = f10) |
|
|
|
|
|
|
|
||
(логическая |
|
|
|
|
|
|
|
|
|||||
1 |
1 |
|
1 |
|
|
|
|
Повторитель |
|
||||
операция ДА) |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Функция f6. |
|
|
|
|
|
|
X1 |
|
|
X1 |
|
||
Неравнознач- |
|
|
|
|
|
|
=1 |
f6 |
f6 |
||||
x1 |
x2 |
f6 |
|
|
X2 |
X2 |
|||||||
ность, |
___ |
|
|
|
|
||||||||
сложение по |
0 |
0 |
|
0 |
f6 = X1 · X2 ˅ |
|
|
|
|
|
|
|
|
|
|
___ |
|
|
|
|
|
|
|
||||
модулю 2 |
0 |
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
˅ X1 · X2 |
|
|
|
|
|
|
|
|||||
(логическая |
1 |
0 |
|
1 |
|
|
|
|
|
|
|
||
|
|
__ |
Сумматор по модулю 2 |
||||||||||
операция |
1 |
1 |
|
0 |
(f6 = X1 X2 = f9) |
||||||||
|
|
(ЛЭ Исключающее |
|
||||||||||
Исключаю- |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
ИЛИ) |
|
|||
щее ИЛИ) |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
Функция f7. |
x1 |
x2 |
f7 |
|
|
X |
1 |
|
|
|
1 |
f7 |
|
|
|
1 |
f7 |
|
|
||||||||
|
|
|
X |
|
|||||||||
Дизъюнкция |
0 |
0 |
|
0 |
f7 = X1 |
˅ X2 |
|
|
2 |
|
|||
|
X |
|
|
|
|
||||||||
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
(логическая |
0 |
1 |
|
1 |
|
__ |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
операция |
1 |
0 |
|
1 |
(f7 = X1 + X2 = f8) |
|
|
|
|
|
|
|
|
ИЛИ) |
1 |
1 |
|
1 |
|
|
Дизъюнктор (ЛЭ ИЛИ) |
||||||
Функция f8. |
|
|
|
|
|
|
X1 |
1 |
f8 |
X1 |
f8 |
||
Отрицание |
x1 |
x2 |
f8 |
|
|
|
|
|
|
||||
|
|
X2 |
|
|
X2 |
|
|||||||
дизъюнкции |
__________ |
|
|
|
|||||||||
0 |
0 |
|
1 |
|
|
|
|
|
|
|
|||
(стрелка |
|
f8 = X1 ˅ X2 |
|
|
|
|
|
|
|
||||
0 |
1 |
|
0 |
|
|
|
|
|
|
|
|||
Пирса), |
|
|
__ |
|
|
|
|
|
|
|
|||
1 |
0 |
|
0 |
(f8 = X1 ↓ X2 = f7) |
|
|
|
|
|
|
|
||
логическая |
|
|
Элемент Пирса (ЛЭ |
|
|||||||||
1 |
1 |
|
0 |
|
|
|
|
||||||
операция |
|
|
|
|
|
||||||||
|
|
|
|
|
ИЛИ-НЕ) |
|
|||||||
|
|
|
|
|
|
|
|
|
|||||
ИЛИ-НЕ |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Функция f9. |
|
|
|
|
|
|
X1 |
|
|
X1 |
|
||
Равнознач- |
|
|
|
|
|
|
=1 |
f9 |
f9 |
||||
|
|
|
|
|
|
|
|
X2 |
|||||
ность, сложе- |
x1 |
x2 |
f9 |
|
|
X2 |
|
|
|
||||
ние по моду- |
___ |
___ |
|
|
|
|
|
|
|
||||
0 0 |
1 |
f9 = X1 · X2 ˅ |
|
|
|
|
|
|
|
||||
лю 2 с отри- |
|
|
|
|
|
|
|
||||||
0 |
1 |
|
0 |
˅ X1 · X2 |
|
|
|
|
|
|
|
||
цанием (логи- |
|
|
|
|
|
|
|
|
|||||
1 |
0 |
|
0 |
|
__ |
|
|
|
|
|
|
|
|
ческая опера- |
|
(f9 = X1 X2 = f6) |
|
|
|
|
|
|
|
||||
1 |
1 |
|
1 |
|
Эквивалентор (ЛЭ |
|
|||||||
ция Исклю- |
|
|
|
|
|
||||||||
|
|
|
|
|
|
Исключающее ИЛИ-НЕ) |
|||||||
чающее |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ИЛИ-НЕ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
36 |

Продолжение таблицы 1.7
1 |
|
2 |
|
|
3 |
|
Функция f10. |
|
|
|
|
|
|
x1 |
x2 |
f10 |
|
|
|
|
Отрицание |
|
|
|
|||
0 |
0 |
1 |
|
___ |
|
|
второго |
|
f10 = X2 |
||||
0 |
1 |
0 |
|
|||
аргумента |
|
___ |
__ |
|||
1 |
0 |
1 |
|
(f10 = X2 = f5) |
||
(логическая |
|
|||||
1 |
1 |
0 |
|
|
|
|
операция НЕ) |
|
|
|
|||
|
|
|
|
|
|
|
Функция f11. |
|
|
|
|
|
|
x1 |
x2 |
f11 |
|
|
|
|
Импликация |
|
|
|
|||
0 |
0 |
1 |
|
f11 = X1 ˅ ̅̅̅ |
||
от X2 к X1 |
|
|||||
0 |
1 |
0 |
|
|||
(логическая |
|
|
__ |
|||
1 |
0 |
1 |
|
(f11= X2 → X1 = f4) |
||
операция |
|
|||||
1 |
1 |
1 |
|
|
|
|
НЕТ-НЕ) |
|
|
|
|||
|
|
|
|
|
|
|
Функция f12. |
|
|
|
|
|
|
x1 |
x2 |
f12 |
|
|
|
|
Отрицание |
|
___ |
|
|||
0 |
0 |
1 |
|
|
||
первого |
|
f12 = X1 |
|
|||
0 |
1 |
1 |
|
|
||
аргумента |
\ |
___ |
__ |
|||
|
1 |
0 |
0 |
|
||
(логическая |
|
(f12 = X1 = f3) |
||||
1 |
1 |
0 |
|
|||
операция НЕ) |
|
|
|
|||
|
|
|
|
|
|
|
|
|
4 |
|
5 |
X2 |
1 |
f10 |
X2 |
f10 |
Инвертор (ЛЭ НЕ)
X |
1 |
1 |
f11 |
X |
1 |
f11 |
|
|
|
||||||
|
|
|
|||||
|
|
|
|
|
|||
X |
2 |
|
|
X |
2 |
|
|
|
|
|
|
|
|
||
Импликатор
X1 |
1 |
f12 |
X1 |
f12 |
Инвертор (ЛЭ НЕ)
Функция f13. |
|
|
|
|
|
|
x1 |
x2 |
f13 |
|
|
||
Импликация |
|
|
||||
0 |
0 |
1 |
___ |
|||
от X1 к X2 |
|
f13 = X1 ˅ X2 |
||||
0 |
1 |
1 |
|
|||
(логическая |
|
|
||||
1 |
0 |
0 |
|
(f13= X1 → X2 = ̅) |
||
операция |
|
|||||
1 |
1 |
1 |
|
|
||
НЕТ-НЕ) |
|
|
||||
|
|
|
|
|
||
Функция f14. |
|
|
|
|
|
|
Отрицание |
|
|
|
|
|
|
x1 |
x2 |
f14 |
|
|
||
конъюнкции |
|
|
||||
0 |
0 |
1 |
_________ |
|||
(штрих |
|
f14 = X1 · X2 |
||||
0 |
1 |
1 |
|
|||
Шеффера, |
|
|
(f14 = X1 | X2 = ̅) |
|||
|
1 |
0 |
1 |
|
||
логическая |
|
|
||||
|
1 |
1 |
0 |
|
|
|
операция И- |
|
|
|
|||
|
|
|
|
|
|
|
НЕ) |
|
|
|
|
|
|
X |
|
|
X |
|
||
|
1 |
|
|
|
||
|
|
1 |
f13 |
|
1 |
f13 |
|
|
|
|
|||
X |
2 |
|
|
X |
2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
Импликатор
X1 |
& f14 |
X1 |
|
|
f14 |
|
||||
|
|
|
||||||||
|
|
|
|
|
|
|
||||
X2 |
X2 |
|
||||||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Элемент Шеффера (ЛЭ И-НЕ)
37

Окончание таблицы 1.7
1 |
|
|
2 |
|
|
3 |
|
|
|
|
|
|
|
Функция f15. |
|
x1 |
x2 |
f15 |
|
|
Константа |
|
0 |
0 |
1 |
|
f15 = 1 |
единица |
|
0 |
1 |
1 |
|
|
|
|
__ |
||||
(логическая |
|
|
|
|
|
(f15 = 1 = f0) |
|
1 |
0 |
1 |
|||
операция 1) |
|
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
4 |
|
5 |
G |
f |
|
|
15 |
|
1 |
|
|
|
|
|
Генератор единицы
– Переместительный (коммутативный) закон справедлив как для дизъ-
юнкции, так и для конъюнкции. Например, для двух аргументов можно записать:
X X |
2 |
X |
2 |
X |
; |
|
1 |
|
|
1 |
|
||
X |
X |
2 |
X |
2 |
X . |
|
1 |
|
|
1 |
|
||
(1.13)
(1.14)
Справедливость выражений (1.13) и (1.14) можно доказать подстановкой в них различных значений X1 и X2 . Закон будет справедлив при любом числе аргументов.
– Сочетательный (ассоциативный) закон также является симметричным,
т. е. справедлив и для дизъюнкции, и для конъюнкции. При логическом сложении (умножении) нескольких аргументов любую группу слагаемых (сомножителей) можно заменить их логической суммой (логическим произведением).
Для трех аргументов можно записать: |
|
|
X1 |
˅ X2 ˅ X3 = X1 ˅ (X2 ˅ X3) = X2 ˅ (X1 ˅ X3) = X3 ˅ (X1 ˅ X2); |
(1.15) |
X1 |
∙ X2 ∙ X3 = X1 ∙ (X2 ∙ X3) = X2 ∙ (X1 ∙ X3) = X3 ∙ (X1 ∙ X2). |
(1.16) |
– Распределительный (дистрибутивный) закон в алгебре логики (в отли-
чие от обычной алгебры) также является симметричным относительно сложения и умножения, т. е. справедливы его разновидности для логического умножения относительно логического сложения (распределительный закон первого рода) и для логического сложения относительно логического умножения (распределительный закон второго рода). Для трех аргументов распределительный закон первого рода можно записать:
(X1 X2 ) X3 X1 X3 X2 X3. |
(1.17) |
|
38 |

Формула (1.17) справедлива и для большего числа слагаемых в скобках. Для доказательства справедливости выражения (1.17) следует рассмотреть условия обращения в 0 или в 1 левой и правой частей.
Для трех аргументов в соответствии с распределительным законом второго рода можно записать:
X |
X |
2 |
X |
(X X ) (X |
2 |
X ). |
(1.18) |
|
1 |
|
3 |
1 |
3 |
3 |
|||
Справедливость формулы (1.18) можно доказать путем непосредственных преобразований. Для этого преобразуем ее правую часть в соответствии с распределительным законом первого рода.
(X1 ˅ X3) ∙ (X2 ˅ X3) = X1 ∙ X2 ˅ X3 ∙ X2 ˅ X1 ∙ X3 ˅ X3 ∙ X3 =
=X1 ∙ X2 ˅ X3 ∙ (X2 ˅ X1 ˅ 1) = X1 ∙ X2 ˅ X3 ∙ 1 = X1 ∙ X2 ˅ X3.
Врезультате преобразований мы пришли к левой части формулы (1.18), что
итребовалось доказать.
– Закон инверсии (правило де Моргана), как и все предыдущие, симметри-
чен относительно логических сложения и умножения.
Отрицание логической суммы нескольких аргументов равно логическому произведению отрицаний этих же аргументов:
X X |
2 |
... |
X |
n |
X |
1 |
X |
2 |
... |
X |
n |
. |
1 |
|
|
|
|
|
|
|
(1.19)
Отрицание логического произведения нескольких аргументов равно логической сумме отрицаний этих же аргументов:
X |
X |
2 |
... |
X |
n |
X |
1 |
X |
2 |
... |
X |
n |
. |
1 |
|
|
|
|
|
|
|
|
(1.20)
Доказательство справедливости выражений (1.19) и (1.20) не представляет трудностей, поскольку левые и правые части равны 0 либо 1 при одинаковых условиях.
–Правило старшинства логических операций является следствием закона инверсии и устанавливает очередность выполнения логических операций в логических функциях, т. е. логические операции обладают приоритетом и выполняются в следующей очередности:
–одиночное отрицание;
–конъюнкция;
–дизъюнкция, сложение по модулю 2 и т. д.;
–общее отрицание.
39

Всякое отклонение от этого порядка должно быть обозначено скобками.
– Правило склеивания обеспечивает упрощение логических выражений и является следствием распределительных законов. Для двух аргументов можно записать:
(X X |
) (X X |
2 |
) X ; |
|
1 |
2 |
1 |
1 |
|
|
|
|
X |
|
X |
2 |
X X |
2 |
X . |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
1 |
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||
Докажем справедливость выражений (1.21) и (1.22): |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
(X1 X2 ) (X1 X 2 ) X1 X1 X2 X1 X1 X 2 X2 X 2 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
X1 (1 X2 X 2 ) X1 1 X1; |
||||||||||||||
X |
X |
2 |
X |
X |
2 |
|
X |
(X |
2 |
X |
2 |
) X |
1 X . |
||||||||||
1 |
|
1 |
|
|
1 |
|
|
|
|
1 |
1 |
|
|
||||||||||
(1.21)
(1.22)
Наименование правила удачно характеризует операцию замены соседних логических сумм (произведений) их общей частью, т. е. два исходных выражения как бы «склеиваются» в одно.
– Правило поглощения также позволяет упрощать логические выражения и является следствием распределительных законов. Для двух аргументов можно записать:
X (X X |
) X ; |
|
|
|
|
|
|
|
|
|
||||
1 |
1 |
|
2 |
1 |
|
|
|
|
|
|
|
|
|
|
X X X |
2 |
X . |
|
|
|
|
|
|
|
|
|
|
||
1 |
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
Докажем справедливость выражений (1.23) и (1.24): |
|
|
|
|
||||||||||
X |
(X X |
) X |
X X |
X |
2 |
X X |
X |
2 |
|
|||||
1 |
1 |
|
2 |
1 |
1 |
1 |
|
|
1 |
1 |
|
|
||
|
|
|
|
X |
(1 X |
) X |
1 X |
; |
|
|
|
|||
|
|
|
|
1 |
2 |
|
|
|
1 |
1 |
|
|
|
|
X1 X1 X2 X1 (1 X2 ) X1 1 X1.
(1.23)
(1.24)
Название рассмотренного правила удачно характеризует операцию замены двух членов логического выражения одним из них.
40
