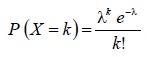СМО с ограничением по времени

Система массового обслуживания с ограниченным по

времени ожиданием

Ожидание наступления обслуживания может быть ограничено двумя условиями: длиной очереди и временем. Во втором случае заявка покидает систему необслуженной, если время ее ожидание превысило некоторое значение TOMax , в противном случае – поступает в канал обслуживания (рис. 1).

Если время ожидания заявок равно нулю, то система называется СМО без ожидания (рис. 2). В качестве примера можно привести поступление телефонных звонков в справочную службу: если оператор занят разговором с другим клиентом, то поступившие в этом период звонки получают отказ в обслуживании.

Рис. 1.– Система массового обслуживания с ограниченным по времени

ожиданием

Рис. 2 – Система массового обслуживания без ожидания

Считая, что время между заявками и обслуживания является случайной величиной с показательным законом распределения, выполним имитацию данной системы со следующими исходными данными: tz =8 мин., to =7 мин.; t0 =9 ч.; TOMax = 1 мин. Результаты представлены на рис. 3. В столбце « Поступление на обслуживание≫ принимается решение о том, будет ли начато обслуживание заявки. Для этого рассчитывается промежуток времени между поступлением заявки и освобождением канала и сравнивается с максимальным временем ожидания заявки.

Е9=ЕСЛИ((МАКС(G$8:G8)-C9)>$D$4;"Нет";"Да").

В случае поступления заявки на обслуживание определяется время его начала и окончания

F9=ЕСЛИ(D9= ≪Да≫;МАКС(C9;G$8:G8); ≪≫)

G9=ЕСЛИ(ЕТЕКСТ(F9);≫≫;F9+D9).

В последнем столбце «Ожидание» рассчитывается время ожидания (для всех заявок, независимо от того, были ли они обслужены)

H9=ЕСЛИ(ЕТЕКСТ(G9);МАКС(G$8:G8;C9)-C9;F9-C9).

Так, из рис. 3 видно, что в данной реализации период ожидания шестой заявки превысил максимально допустимое значение, и поэтому обслуживания не произошло.

Рис. 3 – Моделирование системы массового обслуживания с ограниченным по времени ожиданием

Задание

1. Менеджер фирмы принимает заказы от клиентов на выполнение различных работ.

Заказы поступают посредством телефонной связи. Время между двумя звонками является случайной величиной с показательным законом распределения (среднее значение - tz ), время обслуживания (принятия заказа) – случайная величина с нормальным законом распределения (среднее значение - to , среднее квадратическое отклонение - sto ). В том случае, если звонок поступил в то время, когда менеджер занят приемом другого заказа, то он получает отказ в обслуживании. Стоимость заказа клиента равномерно распределена на интервале [ a ; b ].

Выполните моделирование данной системы при следующих исходных данных: tz =15 мин.; to =15 мин.; sto =2 мин.; a =5000 руб.; b =15000 руб.; tn =9

ч. Рассмотрите поступление шести звонков и определите следующие величины: число отказов в обслуживании; общая сумма заказов; время поступления последнего звонка.

2. Проведите 10 экспериментов и рассчитайте величины:

1. среднее число отказов в обслуживании;

2. среднюю сумму заказов;

3. среднее время завершения моделирования (время окончания обслуживания последней заявки).

3. Выполните моделирование, считая, что вероятность совершения заказа клиентом равна P ( P =0,7).

4. Предположите, что фирма наняла еще одного менеджера и вновь поступивший звонок направляется к свободному в данный момент работнику.

5. Пусть новое оборудование фирмы позволяет поступившим звонкам ожидать освобождения менеджера в течение времени TOMax . Выполните моделирование при TOMax =2 мин. (число каналов обслуживания равно единице), рассчитайте среднее число отказов (за 10 реализаций) и сравните данное значение с полученным во втором задании.

6. Рассмотрите ситуацию, когда максимальное время ожидания каждой заявки определяется также поведением клиентов и его значение – случайная величина с дискретным законом распределения:

Значение 0 1 2	0	1	2
Вероятность	0,25	0,5	0,25

Случайной величиной называется переменная величина, которая может принимать те или иные значения в зависимости от случая. Случайные величины обозначают заглавными буквами латинского алфавита (X, Y, Z), а их значения – соответствующими строчными буквами (x, y, z). Случайные величины делятся на прерывные (дискретные) и непрерывные.

Дискретной случайной величиной называется случайная величина, принимающая лишь конечное или бесконечное (счетное) множество значений с определенными ненулевыми вероятностями.

Законом распределения дискретной случайной величины называется функция, связывающая значения случайной величины с соответствующими им вероятностями. Закон распределения может быть задан одним из следующих способов.

1. Закон распределения может быть задан таблицей:

Значения xi	x1	x2	x3	...	xn
Вероятности pi	p1	p2	p3	...	pn

События X = x_i (i = 1, 2, 3,…,n) являются несовместными и единственно возможными, т.е. они образуют полную систему событий. Поэтому сумма их вероятностей равна единице: р₁+р₂+р₃+…+р_n = ∑p_i =1

2. Закон распределения может быть задан аналитически (формулой) P(X = x_i) = ϕ(x_i). Например:

а) с помощью биномиального распределения: P_n(X=k) = С_n^k p^k q^n-k, 0<р<1, k = 0, 1, 2, …, n;

б) с помощью распределения Пуассона:

где λ>0, k = 0, 1, 2, … .

в) с помощью функции распределения F(x), определяющей для каждого значения x вероятность того, что случайная величина X примет значение, меньшее x, т.е. F(x) = P(X < x).

- свойства функции F(x)

3. Закон распределения может быть задан графически – многоугольником (полигоном) распределения (смотри задачу 3).

Отметим, что для решения некоторых задач не обязательно знать закон распределения. В некоторых случаях достаточно знать одно или несколько чисел, отражающих наиболее важные особенности закона распределения. Это может быть число, имеющее смысл «среднего значения» случайной величины, или же число, показывающее средний размер отклонения случайной величины от своего среднего значения. Числа такого рода называют числовыми характеристиками случайной величины.

Основные числовые характеристики дискретной случайной величины:

• Математическое ожидание (среднее значение) дискретной случайной величины M(X)=Σ x_ip_i. Для биномиального распределения M(X)=np, для распределения Пуассона M(X)=λ

• Дисперсия дискретной случайной величины D(X)= M[X–M(X)]² или D(X) = M(X²)−[M(X)]². Разность X–M(X) называют отклонением случайной величины от ее математического ожидания. Для биномиального распределения D(X)=npq, для распределения Пуассона D(X)=λ

• Среднее квадратическое отклонение (стандартное отклонение) σ(X)=√D(X).