Построение и анализ КДА. ДИПЛОМНАЯ РАБОТА

Министерство образования и науки Российской Федерации

САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИМЕНИ Н. Г. ЧЕРНЫШЕВСКОГО

Кафедра теоретических основ информатики и информационных технологий

Построение и анализ КДА, порождающего начальные отрезки характеристической последовательности чисел Фибоначчи

ДИПЛОМНАЯ РАБОТА

Студента 5 курса факультета компьютерных наук и информационных технологий

Синельникова Евгения Александровича

Саратов 2004

Содержание

1

1Порождение и представление последовательностей конечными детерминированными автоматами

Конечные детерминированные автоматы (КДА) образуют фундаментальный класс дискретных моделей как самостоятельные модели и как основные компоненты машин Тьюринга, автоматов с магазинной памятью и других преобразователей информации. Конечный детерминированный автомат определяется на основе функциональных связей четырех множеств: S (множество состояний), X (множество входных сигналов), Y (множество выходных сигналов) и бесконечного множества T = f0; 1; 2; : : :g (множество абстрактных моментов времени).

Определение. Конечным детерминированным автоматом типа Мили называется совокупность пяти объектов:

где S, X и Y конечные непустые множества, а и отображения вида:

со связью элементов S, X и Y в абстрактном времени T = f0; 1; 2; : : :g для t 2 T определяются уравнениями:

s(t + 1) = (s(t); x(t))

(3)

y(t) = (s(t); x(t))

Отображения и получили названия, соответственно функции переходов и функции выходов автомата A. Автоматы с общим множеством входных сигналов составляют класс сравнимых автоматов. Автоматы без выходных сигналов называются автоматами типа Медведева. Свойством jXj = 1 определяется класс автономных автоматов.

Автономный конечный детерминированный автомат B = (S; Y; ; ), где S и Y конечные непустые множества состояний и выходных сигналов, а и отображения вида : S ! S, : S ! Y , функционирует в абстрактном времени T = f0; 1; 2; : : :g в соответствии с уранениями

2

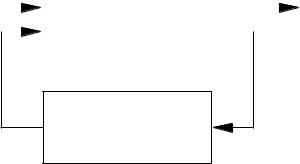
Для каждых начального состояния s(0) = si0 и натурального числа t автомат B определяет две последовательности:

Конечный детерминированный автомат A порождает jXj базовых автономных подавтоматов Ai = (S; fxig; Y; ; ) и таким образом может быть определ¼н как набор автономных компонент по каждому входному сигналу, представляющих собой автономные автоматы Bi = (S; Y; xi ; xi ), ãäå xi (s) =

(s; xi); xi (s) = (s; xi); xi 2 X; s 2 S.

КДА в структурном виде определяется как декомпозиция автомата типа Мили на комбинационную часть и память. При этом предполагается, что множества состояний, входов и выходов закодированы булевыми векторами, комбинационная часть рассматривается как совокупность дискретных преобразователей, реализующих некоторые булевы функции от переменных S и X, блок памяти представляет набор т. н. элементов памяти, задерживающих двоичный сигнал на один такт. Таким образом, автомат представлен, как совокупность функций алгебры логики, реализующих соответственно функцию перехода и функцию выхода (Рис. 1).

s(0)s(1)...s(i)

Рис. 1: Автомат в структурном виде

Конечный автомат может быть представлен как преобразователь входных последовательностей в выходные. При этом выходные последовательности могут рассматриваться как порождаемые, а входные как представляемые.

3

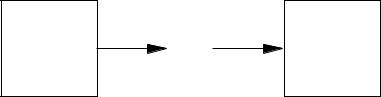
Рис. 2: a) Автономный автомат, порождающий последовательность y(0)y(1)y(2). . . ; б) Автомат Медведева, представляющий слово p

Выходные последовательности автомата определяют множество слов порождаемых этим автоматом. Автономный КДА, называется порождающим, если порождаемое им слово представлено как выходная последовательность (Рис. 2 a), при этом такая последовательность называется порождаемой данным автоматом.

КДА называется представляющим (или принимающим) входное слово p, если на этом входном слове он переходит в множество заключительных состояний, определяемое как подмножество множества его состояний. Такие автоматы могут быть представлены как автоматы типа Медведева (Рис. 2 б).

4

2f -представление последовательностей и чисел

Пусть Ek = f0; 1; : : : ; k 1g è Ek множество всех конечных последовательностей на множестве Ek .

Определение. Последовательность ai1 ; ai2 ; : : : ; aik 2 Ek будем называть f - представимой функцией k-значной логики с порядком рекурентности m

где m < k, если для любого t, m 6 t 6 k, выполняется равенство

Таким образом свойство f -представимости определяет функциональную зависимость, составленную из кортежей, входящих в пересекающиеся подпоследовательности подряд идущих знаков f -представляемой последовательности.

Обозначим различные подпоследовательности последовательности через

где i номер знака, с которого начинается рассматриваемая подпоследовательность, j ее длина.

Функция f -представляющая f -представимую последовательность называется функцией следования, а совокупность функции следования и соответствующей f -представимой последовательности f -представлением.

f -представление последовательности длины n с порядком рекуррентности m обладает следующими свойствами:

подпоследовательности suf i;m+1( ), где i = 0; 1; 2; : : : ; (n m 1), уникальны на всей ;

подпоследовательности suf i;m( ), где i = 0; 1; 2; : : : ; (n m), могут повторяться в и, как набор аргументов, соответствуют определеннмоу значению f -представляющей функции.

Порядок, в котором рассматриваются элементы в последовательности существенно влияет на соответствующее f -представление. Кроме прямого

5

прохода по знакам последовательности рассматривается проход по знакам в обратном порядке. Такое f -представление называется обратным.

При нахождении f -представления для чисел, их рассматривают как последовательности знаков. Иррациональные числа представляются на на- чальных отрезках.

Свойство f -представимости последовательностей оказывается удобным для анализа, когда f -представимость конкретизирована как указанием различных функций, так и в случае f -представимости различных последовательностей одной и той же функцией k-значной логики.

Заметим, что для некоторой f -представимой подпоследовательностиможет существовать несколько функций, задающих ее. Это объясняется тем, что, для данной подпоследовательности c данным числом аргументов, функция f не будет полностью определена (в общем случае на префиксе не будут встречаться подпоследовательности, соответствующие всем возможным значениям аргументов). Вопросы доопределения подобных функций представляют самостоятельную сложность и в данной работе не рассматриваются. При исследовании, функции были доопределены методом дополнения заданным значением. Обратная f -представимость, при исследовании, также не рассматривалась.

6

3Содержательная постановка задачи

В данной работе проводится исследование начальных отрезков бесконечной иррациональной последовательности на предмет f -представимости и представления конечными детерминированными автоматами. Исследуемая последовательность определяется характеристической функцией чисел Фибоначчи на множестве натуральных чисел и представляет собой распределение чисел Фибоначчи в натуральном ряду.

Целью исследования ставится вопрос представления иррациональных последовательностей конечными автоматами. Для полного задания таких последовательностей потребовалось бы бесконечное число состояний КДА, поэтому эти последовательности рассматриваются не полностью, а только на начальных отрезках. Такое ограничение, впрочем, не является недоспутимым для применения на практике. Напротив, все используемые иррациональные числа, представляющие последовательности с бесконечным числом знаков, например число , в практических расчетах берутся в определенном, достаточном приближении.

Инструментом исследования выбрано свойство f -представимости на- чальных отрезков функциями k-значной логики. На содержательном уровне, для f -представимой последовательности с порядком рекурентости m 1, это свойство соответствует функциональной зависимости, в подпоследовательностях m подряд идущих знаков, последнего знака от предшествующих,что означает уникальность подпоследовательностей m подряд идущих знаков на всей последовательности. При этом построение КДА основано на использовании заранее определенной f -представляющей функции соответствующего f -представимого отрезка. Такой подход позволяет рассматривать определяемый автомат как автономный, в котором, отрезки длины порядка рекуррентности представлены как состояния, а в качестве функции выходов берется соответствующая f -представляющая функция.

7

4Формализованная постановка задачи

Рассматриваются натуральный ряд чисел 1; 2; 3; : : : и последовательность чисел Фибоначчи, определяемая следующей формулой:

ãäå u1 = u2 = 1. Обозначим множество чисел Фибоначчи через F.

По распределению чисел Фибоначчи F в натуральном ряду N определяется характеристическая функция g : N ! f0; 1g, имеющая вид:

(

1; n 2 F;

g(n) = (11)

0; n 2= F:

Обозначим характеристическую последовательность знаков f0; 1g, определяемую функцией (11) через , а различные е¼ подпоследовательности, следуя (9), соответственно suf i;j ( ).

Далее в работе рассматривается f -представимость функциями двоич- ной логики начального префикса характеристической иррациональной последовательности , определяемой функцией g на множестве натуральных чисел. Для рассматриваемого начального отрезка, заданной длины, строится f -представление 1; 2; 3; : : :, ãäå k = suf ik ;jk ( ), k = 1; 2; 3; : : :, представляющее собой последовательность подпоследовательностей . Каждой подпоследовательности k ставится в соответствие f -представяющая ее функция fk = (z1; z2; : : : ; zmk ).

На основе заданного f -представления рассматривается построение конечных детерминированных автоматов. При этом все наборы значений аргументов из области определения fk объявляются состояниями автономного КДА.

8

5Характеристическая функция чисел Фибоначчи и f - представление е¼ начальных отрезков

В ходе исследования было проанализировано построение чисел Фибоначчи. Существует как рекуррентная (10), так и аналитческая форма задания чисел Фибоначчи. Аналитическая форма задания определяется формулой Бине [1]

Преимуществом аналитического задания в данном случае является отсутствие необходимости нахождения предыдущих значений для вычисления заданного элемента. Недостатком такого вычисления состоит как в низкой точ- ности связанной с ограничением разрядной сетки, что приводит к ошибкам, так и в сложности вычислений. В данной работе реализованы оба варианта построения, но в качетсве основного берется рекуррентный. В ходе построения было найдено миллионное число Фибоначчи, размер которого составил 208989 десятичных знаков.

Скорость увеличения размерности элементов последовательности чи- сел Фибоначчи такова, что не более, чем через каждые пять элементов, их

размерность увеличивается на один десятичный разряд. По этому поводу

p

имеется теорема [1]. Обозначим a = 1+ 5 .

2

Теорема. Число Фибоначчи u есть ближайшее целое к an , т. е. к n-му члену

n p5

геометрической прогрессии, первый член которой есть a , а знаменатель a.

p

5

Характеристическая функция распределения чисел Фибоначчи в натуральном ряду представляется ноль единичными последовательностями, являющимися начальными отрезками последовательности . Представление характеристической функции определено до 1000000 знака.

Определение последовательности чисел Фибоначчи как геометриче- ской прогрессии позволяет формально определить привед¼нное выше свойство.

Теорема о числе единичных элементов характеристической последовательности чисел Фибоначчи.

Каждая подпоследовательность k = g(10k); : : : ; g(10k+1 1), где k = 0; 1; 2; : : : характеристической последовательности распределения чи-

9