Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный физико-технический университет (МФТИ)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Лекции - Раздел 1

.pdf

Скачиваний:

Добавлен:

03.06.2015

Размер:

933.51 Кб

Скачать

☆

<<< < Предыдущая 1 2 34 / 74 5 6 7 > Следующая >>>

Рассмотрим теперь коэффициент корреляции ry yˆ	между переменными		y и yˆ ,	где
yˆ ˆ ˆ x, а ˆ и ˆ — оценки наименьших квадратов параметров		и гипотетической
линейной связи между переменными x и y . Замечая,	что y yˆ e	(т.к. ei	yi yˆi	по

определению), находим:

ry yˆ

Cov(y, yˆ)

Cov(yˆ e, yˆ)

Cov

(yˆ, yˆ) Cov(e, yˆ)

Var(y) Var(yˆ)

Но ранее мы уже упоминали (при выводе разложения для TSS ) соотношение

yi yˆi yˆi y 0,

i 1

которое, с учетом соотношения yi yˆi 0, приводит к равенству

i 1

n11 yi yˆi yˆi 0, i 1

левая часть которого есть не что иное как Cov(e, yˆ). Следовательно,

ry yˆ

Var(yˆ)

Var(y)

Var(yˆ)

Var(y)

так что

Var(yˆ)

ry yˆ

Var(y)

Последнее соотношение показывает, что коэффициент детерминации равен квадрату коэффициента корреляции между переменными y и yˆ , так что при достаточно сильно

выраженной линейной связи между переменными x и y , что соответствует значению R2 ,

близкому к 1, оказывается близким к 1 и коэффициент корреляции между переменными y и

yˆ .

По причинам, которые будут ясны из дальнейшего рассмотрения, ryyˆ называют

множественным коэффициентом корреляции (multiple-R, множественный-R).

Отметим также, что переменная yˆ измеряется в тех же единицах, что и переменная y , и при изменении масштаба измерения переменной y значение ry yˆ не изменяется.

Отсюда вытекает, что коэффициент детерминации R2 инвариантен относительно изменения масштаба и начала отсчета переменных x и y .

Заметим, наконец, что

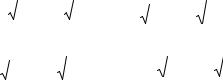
ryyˆ

Cov(y, yˆ)

Cov(y, ˆ ˆ x)

Var(y) Var(yˆ)

Var( ˆ ˆ

Var(y)

ˆ Cov(y,x)

sign( ˆ)

Cov(y,x

)

ˆ 2

Var(y) Var(x)

(Здесь sign(z) 1 для z 0,

sign(z) 0

для z 0,

sign(z) 1

для z 0.)

Поскольку же

Cov(x, y)

Var(x)

то sign( ˆ) sign(Cov(x, y)) и

ry yˆ

sign(Cov(x, y)) rxy ,

так что

r2 r2

R2 .

y yˆ

Из этого соотношения вытекает, что

мы можем вычислить значение R2 еще до непосредственного оценивания модели линейной связи (для этого достаточно вычислить значение коэффициента rxy и

возвести его в квадрат);

значение коэффициента детерминации R2 указывает на степень выраженности

линейной связи между переменными			x и	y (“тесноту линейной связи между x	и
y ”), на качество линейной аппроксимации действительной модели связи между x					и
y	в рассматриваемом диапазоне изменения переменной x, а значение коэффициента
rxy	указывает	и на тесноту линейной		связи между этими переменными	(в
рассматриваемом диапазоне изменения переменной x) и на направление этой связи.
Замечание 1.2
Если rxy 0 , то sign(Cov(y,x)) 1			и ry yˆ	0; если rxy 0, то sign(Cov(y,x)) 1	и
ry yˆ 0, так что всегда		ry yˆ 0.

Приложение П-1.2а

Согласно принципу наименьших квадратов оценки ˆ и ˆ находятся путем минимизации суммы квадратов

Q( , (yi xi )2

i 1

по всем возможным значениям и при заданных (наблюдаемых) значениях x1, ,xn ,

y1, , yn . Точка минимума этой функции двух переменных находится путем приравнивания


нулю частных	производных функции z Q( ,		по переменным	и	,	т. е.
приравниванием	нулю производной функции Q( ,		как функции только	от		при
фиксированном ,
Q( , )/ 0,
и производной функции Q( , как функции только от при фиксированном ,
Q( , )/ 0.
Это приводит к так называемой системе нормальных уравнений (normal equations)
Q( , )/ 0,		Q( , )/ 0,

решением которой и является пара ˆ , ˆ .8 Остается заметить, что согласно правилам

вычисления производных

Q( , )/ 2 (yi xi ) 1 ,

i 1

Q( , )/ 2 (yi xi ) xi ,

i 1

так что искомые значения ˆ и ˆ удовлетворяют паре соотношений

n	n
(yi ˆ ˆ xi ) 0,	(yi ˆ ˆ xi )xi = 0.
i 1	i 1

первое из которых можно записать в виде

(yi yˆi ) 0,

i 1

или

ei 0,

i 1

так что алгебраическая сумма остатков равна нулю.

Эту пару соотношений можно записать также в виде

n ˆ xi yi

i 1

8 Можно проверить, что найденная пара значений действительно обращает указанную сумму квадратов в минимум.

Последняя система является системой двух линейных уравнений с двумя неизвестными

ˆ , ˆ и может быть легко решена, например, методом подстановки.

Из первого уравнения системы находим:

		n			n
ˆ	1	yi	1	ˆ	xi	y	ˆ	x	,
	n		n
		i 1			i 1

так что точка x,y действительно лежит на прямой y ˆ ˆ x . Подстановка полученного выражения для ˆ во второе уравнение системы дает

yi xi n

yixi ,

i 1

откуда

yi xi n

n yixi n y x

yi xi

i 1

Заметим еще, что

2 xi2 2

2 xi2 n

2 ,

i 1

yi y xi x yi xi y xi x yi nyx yi xi nyx.

i 1

Последние соотношения позволяют получить более употребительную форму записи выражения для ˆ (в отклонениях от средних значений):

	n
ˆ	xi	x	yi			y
	i 1						,

	n
	xi			x	2
	i 1

которая в паре с выражением

ˆ y ˆ x

дает явное и простое решение задачи отыскания оценок ˆ , ˆ на основе принципа наименьших квадратов в ситуации, когда не все значения x1, ,xn одинаковы.

Приложение П-1.2б

Имеем:

yˆi yˆi

= yi

yˆi yˆi

i 1

i=1

i 1

ˆ ˆ

i 1

ˆ ei

+ ˆ

yˆi xi

ei .

i 1

i=1

Но

ˆ ˆ

i 1

(см. первое уравнение из системы нормальных уравнений). К тому же

n	yi	xi	n		xi xi	0
yi	yi	xi	yi		xi xi	0
	ˆ			ˆ ˆ
i 1			i 1

(см. второе уравнение из системы нормальных уравнений). Таким образом,

yi yˆi yˆi y 0 .

i 1

Геометрическая интерпретация основных соотношений метода наименьших

квадратов

Основные соотношения метода наименьших квадратов имеют наглядную

геометрическую интерпретацию.

yˆ

Введем в рассмотрение следующие n-мерные векторы: y=

, 1= ,

yˆn

, e=

Тогда

yˆ ˆ 1 ˆ x ,

e y yˆ ,

так что

y yˆ e.

Полученные в Приложении П-1.2а соотношения

n	n
(yi ˆ ˆ xi ) 0,	(yi ˆ ˆ xi )xi = 0
i 1	i 1

можно записать теперь в виде

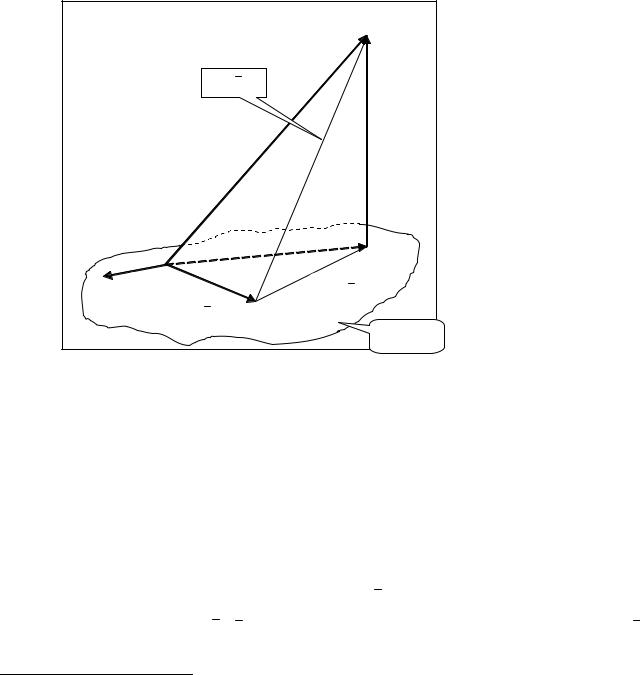
n		n
(ei 1) 0,		ei xi = 0 ,
i 1		i 1
или
e T 1,	eT x = 0 .

Но последние соотношения означают просто, что вектор остатков e ортогонален

единичному вектору 1 и вектору x значений объясняющей переменной x . А это означает,

что он ортогонален порожденному векторами 1 и x двумерному линейному подпространству L2(1, x) n-мерного векторного пространства, в котором расположены все введенные в рассмотрение векторы9.

	B
y y 1
y	e
yˆ	C
A
x	yˆ y 1
y 1	D
	L2 1, x
Рис. 1.9

Вектор	yˆ	является линейной комбинацией векторов			1 и	x, а потому он
принадлежит	L2(1, x). Поскольку же вектор			e ортогонален	L2(1, x),	то он ортогонален
любому вектору,		принадлежащему	L2(1, x),			ˆ
				а значит, ортогонален и вектору y. Таким
образом, в представлении y yˆ e			векторы-слагаемые ортогональны,			а это означает, что

изображенный на рис. 1.9 треугольник ABC – прямоугольный. При этом вектор yˆ является ортогональной проекцией вектора y на L2(1, x).

Предположим, что среднее арифметическое y значений y1, , yn отлично от нуля.

Отложим от точки A вектор y= y 1, получающийся растяжением единичного вектора в y

9 Подпространство L2(1, x) состоит из всех векторов, являющихся линейными комбинациями векторов 1 и x. Условие идентифицируемости обеспечивает неколлинеарность векторов 1 и x.

раз. Этот вектор принадлежит L2(1, x), начинается в точке A и заканчивается в некоторой точке D. Рассмотрим треугольник BCD. Вектор DC является разностью векторов yˆ и y 1, а

потому также принадлежит L2(1, x). Но тогда BC CD (т.к. вектор e ортогонален L2(1, x)),

и треугольник BCD – прямоугольный. По теореме Пифагора получаем: BD 2 CD 2 BC 2 ,

т. е.

y y2 yˆ y2 y yˆ 2 ,

или, в координатной форме,

n			n			n
yi	y	2	yˆi	y	2	yi yˆi 2 .
i 1			i 1			i 1

А это и есть указанное ранее разложение полной суммы квадратов

TSS = ESS + RSS.

Отсюда находим также, что коэффициент детерминации R2 равен

ESS

yˆ y

i 1

cos

BDC .

TSS

y y

	i 1
Заметим также, что соотношение							BC CD означает, что	y yˆ yˆ	y	, или, в
координатной форме,
n
yˆi		y	yi	yˆi 0 .
i 1
Но это именно то соотношение, которое мы выводили в Приложении П-1.2б.
Заметим теперь, что при					y	0	равенство остается	в силе, поскольку оно
принимает в этом случае вид
n		n		n
yi2 yˆi2 yi yˆi 2 ,
i 1	i 1			i 1

а последнее соотношение есть результат применения теоремы Пифагора к прямоугольному треугольнику ABC.

Отметим, наконец, что расположение точки C на рис. 1.9 соответствует ситуации,

когда ˆ 0 и ˆ 0. Ситуация, в которой ˆ 0, но ˆ 0, отличается только тем, что точка

C располагается на той же прямой, на которой располагается вектор x; все приведенные выше рассуждения остаются в силе. Если 0, но ˆ 0, то точка C располагается на той же прямой, на которой располагается вектор 1. Но, как мы установили ранее, в этой ситуации

ˆ y и yˆi y, так что вектор yˆ совпадает с вектором y= y 1. Если при этом y 0, то точка

C совпадает с точкой D,но не совпадает с точкой A. Соотношение опять выполняется,

		n	n
сводясь к тождеству yi y 2 yi y 2 . Наконец, если еще и					y	0, так что и ˆ 0 и
		i 1	i 1
ˆ 0,	то точки	C и	D совпадают с точкой A,	вектор y ортогонален подпространству
L2(1,x),	yˆ 0 и	вектор	e совпадает с вектором y.	Соотношение сводится в этом случае

ктождеству yi2 yi2.

i 1 i 1

Контрольныевопросы

1.Как ставится задача поиска “наилучшей” прямой для аппроксимации линейной модели связи между двумя экономическими переменными?

2.В чем состоит метод наименьших квадратов? Как он реализуется при оценивании параметров линейной модели наблюдений? Что такое система нормальных уравнений, каков ее геометрический смысл?

3.Чему равна алгебраическая сумма остатков, полученных при оценивании параметров линейной модели наблюдений?

4.В каком соотношении находятся знак оценки наименьших квадратов углового

коэффициента модели прямолинейной связи y x

и знак выборочной

ковариации Cov x, y ?

5.Зависит ли значение оценки наименьших квадратов углового коэффициента модели прямолинейной связи y x от выбораединицизмерения переменных x и y ?

6.Какое соотношение существует между полной, объясненной моделью и остаточной суммами квадратов, получаемыми в результате оценивания методом наименьших квадратов линейной модели наблюдений? Каков геометрический смысл этого соотношения?

7.Что такое коэффициент детерминации, и для какой цели он предназначен? В каких границах он изменяется и в каких ситуациях достигает своих граничных значений?

Каков геометрический смысл коэффициента детерминации?

8.Какие переменные называются объясняющими, а какие – объясняемыми?

9.Как связаны значения коэффициента детерминации, получаемого при оценивании

линейной модели наблюдений yi xi i , i 1, ,n, со значениями

множественного коэффициента корреляции и коэффициента корреляции между

переменными x и y ?

10.Что можно сказать о корреляционной связи между остатками и прогнозными значениями объясняемой переменной?

11.Как располагаются точки на диаграмме рассеяния, на которой по оси абсцисс

откладываются прогнозные значения объясняемой переменной, а по оси ординат –

наблюдаемые значения объясняемой переменной?

12.Как располагаются точки на диаграмме рассеяния, на которой по оси абсцисс откладываются наблюдаемые значения объясняемой переменной, а по оси ординат – прогнозные значения объясняемой переменной?

Тема1.3. Примерыподборалинейныхмоделей связимеждудвумяфакторами.Ложная линейнаясвязь.

План лекции

1.Примеры подбора линейных моделей связи между двумя факторами.

2.Ложная линейная связь между двумя экономическими факторами и причины ее возникновения.

3.“Очистка” переменных, частный коэффициент корреляции.

4.“Обратная” модель линейной связи.

5.Пропорциональная связь между переменными.

Текстовыйматериаллекции

Пример 1.3.1

В табл. 1.7 в конце раздела 1 приведены данные об изменении потребительского спроса на куриные яйца семи домашних хозяйств в зависимости от цены на этот продукт в течение 15 недель (спрос измерялся в дюжинах, цена – в долларах).

Диаграмма рассеяния для этих данных имеет следующий вид:

15
Спрос
9
0.35	0.55
	Цена

Рис. 1.10

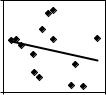
Предполагая, что модель наблюдений имеет вид				yi xi i ,i 1, ,n, где yi
– спрос в i-ю неделю, а	xi	–	цена в i-ю неделю, мы	получаем следующие оценки для
неизвестных параметров			и модели линейной	связи	между ценой и спросом:
ˆ 21.100, ˆ 18.559. Таким			образом, подобранная модель		линейной связи имеет вид
y 21.100 18.559 x . При этом

TSS 17.6, RSS 8.562, ESS 9.038,

так что коэффициент детерминации оказывается равным R2 0.514, т. е. изменчивость цен объясняет 51.4% изменчивости спроса на куриные яйца. На диаграмме рассеяния изображена прямая линия, соответствующая подобранной модели линейной связи.

Пример 1.3.2

В табл. 1.8 в конце раздела 1 приведены данные о годовом потреблении свинины y

на душу населения в США (в фунтах) и оптовых ценах на свинину x (в долларах за фунт) за период с 1948 по 1961 год. Для этих данных диаграмма рассеяния имеет вид:

74
Потребление
59
0.4	0.55
	Цена
	Рис. 1.11

Оценивая модель yi xi i ,i 1, ,n,	где	yi – потребление свинины в i-й
год рассматриваемого периода, а xi – оптовая цена на свинину в этом году,			мы получаем
следующие оценки для неизвестных параметров	и	модели линейной связи между
оптовой ценой и потреблением: ˆ 77.552, ˆ 24.925.		Таким образом,	подобранная
модель линейной связи имеет вид y 77.552 24.925 x . При этом

TSS 208.194, RSS 196.701, ESS 11.493,

так что коэффициент детерминации здесь оказывается равным R2 0.055. Изменчивость оптовой цены объясняет здесь лишь 5.5% изменчивости потребления свинины.

Пример 1.3.3

<<< < Предыдущая 1 2 34 / 74 5 6 7 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
18.11.2019494.59 Кб7КР ПОТОКОВАЯ ФПФЭ_2011.doc
#
20.08.20191.75 Mб16край.doc
#
03.06.201587.53 Кб13курсач лето.docx
#
16.08.2019171.52 Кб3Лабораторная работа Шматков И. Л..doc
#
03.06.2015845.46 Кб43Лебедев, Колоколов. ИГМФ.pdf
#
03.06.2015933.51 Кб9Лекции - Раздел 1.pdf
#
03.06.201514.11 Mб11Лекции по физкинетике.PDF
#
03.06.2015386.05 Кб36Лекции по философии (Семенов) 2006-2007.doc
#
03.06.20151.71 Mб19Лекции.pdf
#
03.06.201583.97 Кб40Лекция Потребности и мотивы.doc
#
03.06.20151.29 Mб27Лекция 1 - конспект.pdf