mathlecnew

4.ПОЛИНОМЫ ЛЕЖАНДРА

При решении задач теории поля или квантовой механики зачастую возникают случаи, когда описывающие поле уравнения обладают симметрией относительно вращений вокруг некоторой точки. В этом слу- чае задача допускает разделение переменных. Поясним это понятие на примере решения уравнения Шр¼дингера для частицы массы m, помещенной в так на-

зываемое центрально-симметричное поле, потенциал которого U зависит только от расстояния r до некото-

рой точки, в которую мы поместим начало координат. Тогда уравнение Шр¼дингера для квантового состояния с энергией E имеет следующий вид

Здесь волновая функция частицы, ~ постоянная Планка, а и ' азимутальный и полярный углы в

сферической системе координат, связанной с выбранной точкой.

Уравнение (4.1) допускает разделение переменных, то есть его решение можно искать в виде произведения

Число m должно быть целым, поскольку волновая функция должна быть периодической функцией ' с периодом 2 . Число n также должно быть целым и n jmj, поскольку только в этом случае функция

может быть регулярной функцией углов. Общее решение уравнения (4.1) в силу его линейности представляется в виде суперпозиции (суммы) членов вида (4.2).

Сначала мы проанализируем простейший случай m = 0. В этом случае уравнение (4.3) сводится к

где 0 < < . Обозначая = cos , мы переписываем уравнение (4.4) в виде

где 1 < < 1. Это уравнение переписывается в виде

P 00 2 (1 2) 1P 0+n(n+1)(1 2) 1P = 0 (где штрих обозначает производную по ), то есть мы имеем дело с оператором Штурма-Лиувилля (2.6).

11

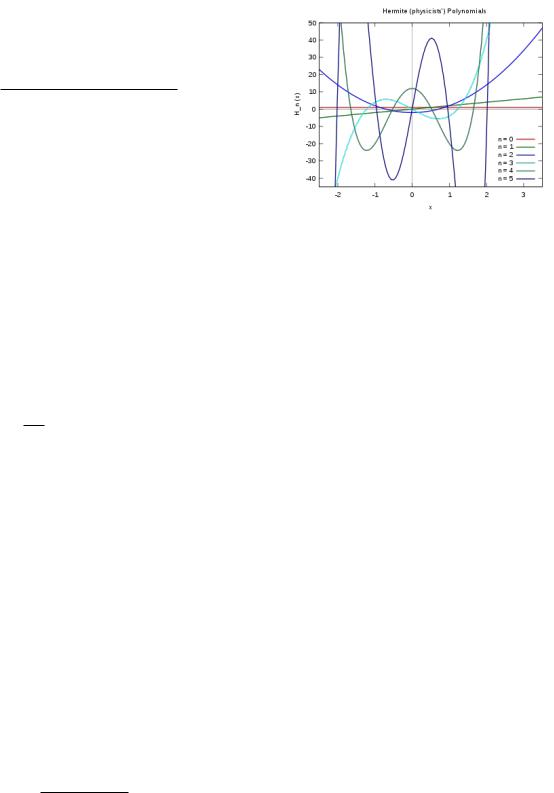
Рис. 2: Несколько первых полиномов Лежандра.

Непосредственной проверкой можно убедиться, что одним из решений уравнения (4.5) являются полиномы Лежандра Pn( ), n = 0; 1; 2 : : : , которые определяются следующим образом

Функция Pn( ) является полиномом n-го порядка, симметричным по при четных n и антисимметрич- ным по при нечетных n. Отметим также равенство Pn(1) = 1. Первые три полинома Лежандра равны

Графики нескольких первых полиномов Лежандра приведены на рисунке 4.6.

Полиномы Лежандра удовлетворяют следующим соотношениям:

(n + 1)Pn+1( ) (2n + 1) Pn( ) + nPn 1( ) = 0;(4.8)

которые проверяются непосредственно, исходя их определения (4.6). Соотношение (4.8) называется рекуррентным, оно позволяет последовательно полу- чать явные выражения для полиномов Лежандра все большего порядка, исходя из первых двух членов в (4.7). Соотношения (4.9) позволяют свести производные от полиномов Лежандра к комбинации самих этих полиномов.

Полиномы Лежандра являются коэффициентами разложения в ряд по t функции (1 2t + t2) 1=2, êî-

торая называется производящей функцией. Выпишем это разложение

p

которое легко проверяется непосредственно. Для коэффициентов разложения ~

Pn( ) это тождество эквивалентно рекуррентному соотношению (4.8). Кроме

того, совпадение первых двух членов разложения, ~

P0

è ~

P1, ñ P0 è P1 (4.7) легко проверяется непосредствен-

но. Отсюда следует совпадение всех членов разложения ~

Pn( ) ñ Pn( ), поскольку рекуррентное соотноше-

ние (4.8) позволяет однозначно построить все высшие полиномы из первых двух. Аналогично анализируется разложение производящей функции по обратным степеням t. В результате мы приходим к соотношени-

ÿì

(4.10) Первый из этих рядов сходится при jtj < 1, а второй

при jtj > 1, если действительное число и j j < 1.

Соотношение (4.10) можно использовать для полу- чения интегрального представления для полиномов Лежандра. Воспользовавшись теоремой о вычете, мы находим из соотношения (4.10)

где интеграл идет против часовой стрелки по небольшому замкнутому контуру, охватывающему начало координат. Корень квадратíûé èмеет точки ветвле-

ло и j j < 1. Эти точки ветвления можно предста-

вить в виде t = exp( i ), где = cos . Таким образом, разрез функции (1 2t +t2) 1=2 можно провести

вдоль дуги единичной окружности в плоскости t, которая определяется условиями < # < 2 , где предполагается лежащим в интервале 0 < < , а #аргумент t. Деформируя теперь контур интегриро-

вания в приведенном выше интеграле так, чтобы онсел на разрез, мы находим следующее интегральное представление

Интегральное представление (4.11) позволяет найти асимптотическое выражение для полиномов Лежандра при больших n. В этом случае в силу быстрой ос-

цилляции sin[(n + 1=2)#] главный вклад в интеграл

набирается вблизи нижнего предела интегрирования из-за знаменателя в (4.11). Подставляя # = + x, рас-

кладывая по x подынтегральное выражение и устрем-

ляя затем верхний предел интегрирования к бесконеч- ности, мы находим

12

Вычисляя здесь интеграл по x, мы находим асимптотическое выражение

Выражение (4.13) можно получить также методом WKB (смотри ниже), который работает как раз при больших n. Чтобы применить этот метод, перепишем

уравнение (4.4) в терминах переменной t = ln tan( =2). Тогда оно принимает вид уравнения (4.20):

Таким образом

p = i(n + 1=2)= cosh t = i(n + 1=2) sin ;

Z

S = dt p(t) = i(n + 1=2) ;

неравенство

вает применение метода WKB. Суммируя теперь два множителя (4.21), мы и получаем выражение (4.13). Разумеется, приведенным методом невозможно полу- чить общий множитель и сдвиг фазы.

Рассмотрим теперь произвольное решение уравнения (4.5), регулярное в точке = 1, когда оно разлага-

ется в ряд Тейлора по x = 1. Перепишем уравнение (4.5) в терминах переменной x:

(2x + x2)P 00 + 2(1 + x)P 0 n(n + 1)P = 0;

где штрих означает дифференцирование по x. Под-

ставляя в это выражение разложение в ряд по x, P = Pk pkxk, мы находим рекуррентное соотношение

2(k + 1)2pk+1 = [n(n + 1) k(k + 1)]pk:

Таким образом, при целом n цепочка обрывается на k = n, и решение оказывается конечным полино-

мом, который (с точностью до множителя) совпадает с Pn( ). Если же n не является неотрицательным це-

лым числом, то в разложении присутствуют все степени x. В пределе больших k мы имеем pk+1 = (1=2)pk.

Отсюда следует, что радиус сходимости этого ряда равен 2, и, более того, он приводит к простому полюсу

при x = 2, то есть = 1. Таким образом, мы дока-

зали, что полиномами Лежандра исчерпываются решения уравнения (4.5), регулярные как в точке = 1,

так и в точке = 1.

Как следует из уравнения (4.5), полиномы Лежандра являются собственными функциями оператора

который является самосопряженным на классе функций, заданных на интервале 1 < < 1 и остающихся

ограниченными на этом интервале, включая конечные точки. Самосопряженность оператора (4.15), то есть свойство (2.19), легко проверяется интегрированием по частям. Поэтому полиномы Лежандра удовлетворяют условиям ортогональности (2.20):

Z 1

1

если n 6= l. Впрочем, соотношение (4.16) можно про-

верить и непосредственно после подстановки выражения (4.6) и многократного интегрирования по частям. Точно также может быть найдено и условие нормировки

Общее соотношение (2.23) означает, что полиномы Лежандра, как полная система собственных функций оператора (4.15), конечных на интервале ( 1; +1),

удовлетворяют соотношению

k=0

Это соотношение можно непосредственно доказать, если воспользоваться результатом задачи к настоящему разделу, в которой найдено значение суммы (4.18) при конечном числе слагаемых, когда k пробегает от

0 до n. Считая n 1 и пользуясь асимптотическим выражением (4.13), мы находим

где x = cos , y = cos '. При n ! 1 первое слагаемое в фигурных скобках в (4.19) сходится к -функции

(смотри задачу к разделу 2), а второе стремится к нулю из-за нарастания осцилляций косинуса. В результате в пределе n ! 1 мы получаем соотношение

(4.18).

Возвратимся теперь к уравнению (4.3). Его решениями, регулярными в точках = 0; являются так на-

зываемые присоединенные полиномы Лежандра, которые определяются следующим образом

Pnm(cos ) = 2n1n! sinm (d cos )n+m (cos2 1)n:

При m = 0 мы возвращаемся к полиномам Лежандра

(4.6). Присоединенные полиномы Лежандра обладают свойствами, во многом аналогичными свойствам полиномов Лежандра. Мы не будем обсуждать здесь эти свойства, которые можно найти в специальной литературе.

13

A.Метод WKB

Вернемся к однородному уравнению (2.5), где в операторе Штурма-Лиувилля (2.6) Q = 0:

p

Предположим, что величина p = U меняется достаточно медленно на масштабе p 1, что означает вы- полнение неравенства dp=dx p2. Тогда для функции

f можно построить следующее приближенное решение

ãäå C1; C2 некоторые константы. Выражение (4.21)

было получено Вентцелем (Wentzel), Крамерсом (Kramers) и Бриллюэном (Brillouin) и носит название приближения WKB, что является аббревиатурой имен этих авторов.

Подставляя выражение (4.21) в уравнение (4.20),

можно убедиться, что оно является решением, если пренебречь членами с (dp=dx)2 è d2p=dx2. Первое пре-

небрежение возможно в силу предполагаемого нера- венства dp=dx p2, а второе в силу неравенства

d2p=dx2 p dp=dx, которое получается из предыдущего дифференцированием по x.

Фактор U в уравнении (4.20) может быть как отри-

цательным, так и положительным, к обоим этим слу- чаям одинаково применим метод WKB. В первом слу- чае величина p является действительной, и два слага-

емых в выражении (4.21) являются растущей и убывающей по x экспонентами. Во втором случае величина

p является чисто мнимой, и мы имеем дело с экспонентами от мнимых величин S. Другими словами, мы

имеем дело с осциллирующими функциями, если речь идет о действительных решениях.

B.Задачи

Найти уравнение на функцию R(r), фигурирующую в выражении (4.2).

Найти значение P2n(0).

Вывести соотношения (4.8,4.9), исходя из определения (4.6).

Проверить выполнение уравнения (4.5) для по-

линомов Лежандра, исходя из формулы дифференцирования (4.9) и используя рекуррентное соотношение (4.8).

Получить выражение (4.13) из (4.12).

Доказать соотношение

n

X

(2k + 1)Pk(x)Pk(y)

k=0

= (n + 1)Pn(x)Pn+1(y) Pn+1(x)Pn(y): y x

Указание: действовать по индукции с учетом рекуррентного соотношения (4.8).

Найти R0 d P2n(cos ), R0 d sin P2n+1(cos ).

Найти R 11 dx x2Pn 1(x)Pn+1(x).

Найти разложение в ряд по полиномам Лежандра Pn(x) монома xk.

5.ПОЛИНОМЫ ЭРМИТА

Полиномы Эрмита естественно возникают в зада- че о квантовом осцилляторе, которая является одной из базисных задач квантовой механики. Одномерная квантовая частица, движущаяся в квадратичном потенциале (это и есть осциллятор), описывается следующим стационарным уравнением Шр¼дингера

где первый член кинетическая энергия, второй членпотенциальная энергия, а E энергия частицы. После подстановки = exp( x2=2)u уравнение (5.1) сво-

дится к виду

которое мы и исследуем в дальнейшем. Отметим, что оператор в (5.2) относится к типу Штурма-Лиувилля (2.6).

Уравнение (5.2) инвариантно относительно замены x ! x и потому имеет четные и нечетные решения.

Четное решение может быть разложено в ряд по четным степеням x:

1

X

u = akx2k:

k=0

Подставляя это выражение в уравнение (5.2) и приравнивая коэффициенты при степенях x, мы находим

рекуррентное соотношение

2k n

ak+1 = (k + 1)(2k + 1)ak;

которое позволяет последовательно вычислять коэффициенты разложения u в ряд по x. При больших

u / exp(x ) на больших x. Единственным исключе- нием являются четные n, тогда ряд по x обрывается

14

Рис. 3: Несколько первых полиномов Эрмита.

на k = n=2, и мы имеем дело с конечным полино-

мом. Аналогичным образом можно показать, что ряд по нечетным степеням x, представляющий нечетное

решение уравнения (5.2), обрывается, если n нечетно.

Таким образом, мы приходим к выводу, что уравнение (5.2) имеет решения в виде конечных полиномов при неотрицательных целых n.

Непосредственная проверка, то есть подстановка в уравнение (5.2), показывает, что при неотрицательных целых n полиномиальные решения уравнения

(5.2) сводятся к полиномам Эрмита, которые определяются следующим выражением

Отсюда получаются следующие значения полиномов Эрмита в нуле

H2n(0) = ( 1)n2n(2n 1)!!; H2n+1(0) = 0; (5.4)

где (2n 1)!! (2n 1)(2n 3) : : : . Первые полиномы Эрмита записываются в следующем виде

H0(x) = 1; H1(x) = 2x; H2(x) = 4x2 2: (5.5)

Графики нескольких первых полиномов Эрмита приведены на рисунке 3.

Рассмотрим сумму

1

X

(tn=n!)Hn(x);

n=0

которая после подстановки определения (5.3) дает разложение в ряд Тейлора exp[ (x t)2]. С использо-

ванием этого результата мы приходим к соотношению

Таким образом, функция в левой части соотношения (5.6) является производящей функцией полиномов Эрмита. Дифференцируя соотношение (5.6) по x,

мы находим выражение для производной

Далее, беря производную по t от соотношения (5.6) и приравнивая коэффициенты при степенях t, мы полу- чаем

Это рекуррентное соотношение позволяет последовательно вычислять полиномы Эрмита.

Для полиномов Эрмита справедливо интегральное

Для доказательства заметим, что представление (5.9) воспроизводит соотношение (5.7), а также удовлетворяет (5.4). Таким образом, мы можем по индукции, переходя от n 1 к n, обосновать представление (5.9).

Представляя подынтегральное выражение в соотношении (5.9) exp[n ln(x + it) t2] и используя для боль-

ших n метод перевала, мы находим (суммируя вклады от двух перевальных точек) выражение

p

Hn(x) 2 (2n=e)n=2 exp(x2=2)

справедливое при n x; 1.

Возвратимся теперь к уравнению (5.1). Функцииn(x) / exp( x2=2)Hn(x) составляют полный набор

решений этого уравнения, стремящиеся к нулю при x ! 1. В силу того, что оператор в левой части

уравнения (5.1) является самосопряженным на этом классе функций, то n являются ортогональными, то

R

åñòü dx n(x) m(x) = 0, если n 6= m. Отнормируем теперь функции n(x) так, чтобы этот набор был ор-

R

тонормированным: dx n(x) m(x) = mn. Для этого воспользуемся выражением

Отсюда находим ортонормированный базис

Докажем теперь полноту базиса (5.12). Для этого

15

Сумма по n представляет собой ряд Тейлора, который собирается в exp[ (y + iq=2)2]. Подставляя этот результат в полученную выше формулу, мы находим

X

n(x) n(y) = exp(x2=2 y2=2)

n

Z +1 dq exp[iq(x y)] = (x y);

1 2

что завершает доказательство полноты.

Таким образом, любую функцию f(x), заданную на действительных x и не слишком быстро стремящуюся к бесконечности при x ! 1, можно разложить в ряд по базису (5.12):

Это разложение можно переписать в терминах полиномов Эрмита

A.Метод перевала

Метод перевала применим к интегралам типа

Z b

a

при выполнении определенных условий на функцию S(z). Прежде всего мы будем предполагать, что функ-

ция S(z) аналитична вблизи пути интегрирования от a к b и, следовательно, контур интегрирования можно деформировать в области аналитичности S(z). Далее,

мы будем предполагать, что в области аналитичности

имеется по крайней мере одна точка с нулевой производной S0(z0) = 0 и что контур интегрирования мож-

но деформировать таким образом, чтобы он проходил через z0, причем действительная часть S(z) должна достигать в точке z0 максимума при движении вдоль деформированного контура. Тогда точка z0 называет- ся седловой, поскольку для направления, перпендикулярного контуру, действительная часть S(z) достига-

ет в точке z0 минимума.

Если в седловой точке действительная часть S(z)

достигает абсолютного максимума вдоль контура интегрирования, то можно надеяться, что именно окрестность седловой точки даст главный вклад в интеграл (5.15). Разложим S в ряд Тейлора вблизи седловой точки: S S0 + S000(z z0)2=2, ãäå S0 è S000 значения функции S и ее второй производной в точ-

êå z = z0. Если S достаточно быстро меняется вблизи

седловой точки, то главный вклад в интеграл дает узкая окрестность седловой точки z = z0, и мы можем

ограничиться в интеграле (5.15) этим разложением, распространив интегрирование до бесконечности в обе стороны. Тогда мы приходим к Гауссовому интегралу, который дает

Подчеркнем, что обе величины, S0 è S000, могут быть комплексными. Знак перед квадратным корнем определяется направлением, в котором контур интегрирования проходит через седловую точку. Условием применимости приближения (5.16) является значительное изменение функции S(z) в области применимости

приведенного разложения, то есть jS000jR2 1, где Rрадиус сходимости разложения функции S(z) в ряд

Тейлора около точки z = z0.

В области аналитичности функции S(z) может ока-

заться несколько седловых точек. В этом случае надо выбрать ту из них, в которой ReS0 максимальна, по-

скольку именно окрестность этой точки дает главный вклад в интеграл (5.15). Возможно также вырождение, когда действительные части S в нескольких сед-

ловых точках одинаковы (или мало отличаются). Тогда для оценки интеграла (5.15) надо брать сумму выражений (5.16) для этих седловых точек.

B.Задачи

Доказать, что старший член разложения Hn(x) имеет вид 2nxn.

Найти значение интеграла

Z +1

dx exp( x2)H2n(xy):

1

Найти значение интеграла

Z +1

dx exp[ (x y)2]Hn(x):

1

Найти значение интеграла

Z +1

dx x exp( x2)H2n 1(xy):

1

Найти значение интеграла

Z +1

dx xn exp( x2)Hn(xy):

1

Примечание: Ответ выражается через полиномы Лежандра.

16

Найти значение интеграла

Z +1

dx exp( x2) sinh( x)H2n+1(x):

0

Найти значение интеграла

Z +1

dx exp( x2) cosh( x)H2n(x):

0

Доказать соотношение

Hn(x) = exp 1 d22 (2x)n:

4 dx

Указание: просуммировать по n правую часть этого соотношения с весом tn=n! и показать, что

эта сумма сводится к левой части соотношения (5.6).

Доказать соотношение (5.11). Указание: составить комбинацию exp( t2 +2tx s2 +2sx), âûðà-

зить ее через двойную сумму по полиномам Эр-

мита из соотношения (5.6) и проинтегрировать получившееся равенство по x с весом exp( x2).

На этом пути получатся и соотношения ортогональности.

6.ВЫРОЖДЕННАЯ ГИПЕРГЕОМЕТРИЧЕСКАЯ ФУНКЦИЯ

Вырожденная гипергеометрическая функция( ; ; z) (con uent hypergeometric function) возника-

ет во многих задачах математической физики. Она является решением вырожденного гипергеометриче- ского уравнения

где и произвольные параметры. Уравнение (6.1) переписывается в виде u00 + ( =z 1)u0 ( =z)u = 0,

то есть мы снова сталкиваемся с оператором ШтурмаЛиувилля (2.6). Функция ( ; ; z) характеризуется

тем, что она аналитична в точке z = 0 и имеет единичное значение в нуле: ( ; ; 0) = 1.

функции ( ; ; z) в ряд Тейлора около точки z = 0. Вычисляя последовательно коэффициенты этого

с очевидным способом построения коэффициентов ряда. При неотрицательных целых ряд (6.2) обры-

вается и ( ; ; z) сводится к полиному. При больших n отношение коэффициентов при степенях zn è zn 1 в разложении (6.2) стремится к 1=n. Поэто-

му ряд (6.2) сходится на всей плоскости комплексного переменного, то есть единственной особенностью вырожденной гипергеометрической функции является бесконечность, которая является существенной особой точкой ( ; ; z).

При неотрицательных целых ряд (6.2) обрыва-

ется и вырожденная гипергеометрическая функция( ; ; z) сводится к полиному. В частности справед-

ливы соотношения

которые сводят полиномы Эрмита к вырожденной гипергеометрической функции.

Уравнение (6.1) является дифференциальным уравнением второго порядка и потому имеет два линейно независимых решения, одним из которых является вырожденная гипергеометрическая функция( ; ; z). Второе независимое решение можно найти,

заметив, что если u удовлетворяет уравнению (6.1), то z 1u также удовлетворяет вырожденному гипергеометрическому уравнению с коэффициентами 0 =

+ 1, 0 = 2 . Таким образом, общим решением уравнения (6.1) является

u = c1 ( ; ; z) + c2z1 ( + 1; 2 ; z); (6.5)

ãäå c1 è c2 произвольные константы. При = 1 оба

члена в сумме (6.5) совпадают. Этот случай требует особого рассмотрения, тогда в общем решении возникает дополнительный логарифмический множитель.

Уравнение (6.1) является дифференциальным уравнением, в котором переменная z входит линейно.

В этом случае можно при помощи метода Лапласа (смотри ниже) найти интегральное представление решения этого уравнения. Составляем функции P и Q

в соответствии с выражениями (6.17): P = t , Q = t(t 1), и далее находим Z = t 1(t 1) 1.

Таким образом, решение уравнения (6.1) может быть записано в виде контурного интеграла

Z

u = dt etzt 1(t 1) 1:

C

Применяя аналогичную процедуру к z 1u, мы находим

Z

u = z1 dt etzt (t 1) :

C

Производя в этом интеграле замену переменной интегрирования tz ! t, мы получаем

Z

u = dt ett (t z) : (6.6)

C

17

Контур C в интеграле (6.6) естественно выбрать так, чтобы он приходил из 1 и возвращался в 1 (об-

ходя каким-то образом особенности подынтегрального выражения, имеющиеся при t = 0 и t = z), тогда

произведение ZQ exp(t) на концах этого контура бу-

дет равно нулю.

Интеграл (6.6) не имеет особенностей при z = 0, ес-

ли он охватывает обе особенности. Выберем контур C, который приходит снизу из 1 огибает особен-

ности справа и возвращался в 1 сверху . Инте-

грал по этому контуру должен с точностью до множителя совпадать с вырожденной гипергеометрической функцией ( ; ; z). Мы считаем, что разрезы функций t и (t z) идут в 1, а значения этих функ-

ций при положительном значении переменной положительны. Тогда значение интеграла при z = 0 равно

При целых отрицательных значениях ряд (6.2) не

определен, так как, начиная с некоторого члена, знаменатель обращается в ноль. Этому соответствует наличие полюса у ( ) в соотношении (6.8). В то же

время сам контурный интеграл в соотношении (6.8) остается конечным при целых отрицательных значе- ниях .

Производя в равенстве (6.8) замену t ! t + z, мы находим соотношение

Дифференцирование по z соотношения (6.8) и инте-

грирование по частям в контурном интеграле позволяет получить ряд соотношений:

При больших положительных z основной вклад в

контурный интеграл в (6.8) определяется окрестностью особой точки t = z. Делая замену переменных t = z + и пренебрегая зависимостью от в t , ìû

находим

где контур C0 приходит из 1 снизу разреза, обходит особую точку = 0 справа и уходит в 1 сверху от

разреза. Этот контурный интеграл сводится к обратной Гамма-функции, и мы получаем окончательно

Асимптотическое выражение (6.13) справедливо и в комплексной области для z с большой положительной

действительной частью.

A.Метод Лапласа

Метод Лапласа позволяет получать интегральные представления решений обыкновенных дифференциальных уравнений для функции Y (x), линейных по

переменной x:

где C некоторый контур в комплексной плоскости t. Подставляя уравнение (6.14) в представление (6.15), используя соотношение x exp(xt) = d exp(xt)=dt

и предполагая, что в интеграле (6.15) можно произвести интегрирование по частям по t без граничных

членов, мы находим уравнение

NN

где в показателе экспоненты стоит первообразная от P=Q (определенная с точностью до константы). По-

скольку P и Q являются полиномами по t, эту перво-

образную можно выразить через элементарные функции.

Выясним теперь условие, при котором возможно упомянутое выше интегрирование по частям. Для этого произведение ZQ exp(xt) должно иметь одно и то

же значение на концах контура C (который может

быть как замкнутым, так и незамкнутым). Наиболее естественным выбором контура C является контур,

который идет вдоль одного из направлений из бесконечности, вдоль которого произведение ZQ exp(xt)

стремится к нулю, и возвращается в бесконесность вдоль другого направления так, чтобы вдоль этого

18

направления произведение ZQ exp(xt) также стреми-

лось к нулю. Число таких направлений растет с увеличением порядка уравнения N, что и обеспечивает

необходимое число независимых решений уравнения (6.14), которые получаются из выражения (6.18) при различных выборах контура интегрирования C.

B.Задачи

Доказать соотношение (6.7).

Доказать ( ; ; z) = exp(z).

Доказать соотношения (6.10,6.11,6.12).

Найти значение ( ; ; z) при целых положительных и , . Указание: в этом случае интеграл (6.8) сводится к вычету в точке t = z.

Найти выражение для полиномов, к которым сводится ( ; ; z) при целых отрицательных в случае целых положительных . Указание: вос-

пользоваться результатом предыдущей задачи и соотношением (6.9).

Найти интеграл

Указание: воспользоваться интегральным представлением (6.8).

Найти второе независимое решение вырожден-

ного гипергеометрического уравнения (6.1) при= 1. Указание: в соответствии с (6.5) при про-

извольном второе независимое решение можно всегда записать в виде

здесь надо перейти к пределу ! 1.

7. УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ

В ряде физических приложений возникают дифференциальные уравнения в частных производных с постоянными коэффициентами. Примерами таких уравнений являются уравнение диффузии и уравнение Шр¼дингера для свободной частицы

При решении таких уравнений весьма эффективным оказывается пространственное преобразование Фурье. В дальнейшем под решением уравнения мы обыч- но имеем в виду решение задачи Коши, то есть восстановление функции, подчиняющейся заданному уравнению, по ее начальному значению. Если не оговорено обратное, за начальный момент времени принимается t = 0.

Мы начнем с уравнения диффузии (7.1). Сделаем Фурье-преобразование по x :

в соотношение (7.3) и беря интегралы по q, мы находим

Соотношение (7.4) в принципе решает задачу Коши, которая заключается в нахождении решения данного дифференциального уравнения по начальному значе- нию функции.

Если начальное поле U(0; x) локализовано вблизи начала координат, то есть если U(0; x) достаточно быстро спадает при росте jxj, то U(t; x) обладает уни-

версальной асимптотикой на больших временах. Что-

бы установить эту асимптотику, мы рассмотрим времена t l2, где l длина, на которой локализовано

поле U(0; x). Это означает, что интеграл (7.4) набирается в области jyj . l. При этом условии можно

пренебречь y в экспоненте в (7.4). В результате мы заключаем, что при t l2

Отметим, что приближение (7.5) соответствует подстановке U(0; y) ! A (y). Если для локализованно-

го вблизи начала координат поля U(0; x) интеграл A (7.6) равен нулю, то асимптотика U(t; x) на боль-

ших временах будет иной. Раскладывая экспоненту в (7.4) по y, мы находим ведущий член разложения при

A = 0:

19

Выражения (7.5,7.7) являются аналогами мультипольного разложения (поля точечного заряда и поля точечного диполя) в электростатике.

Подобная процедура, связанная с пространственным Фурье-преобразованием, может быть проделана и для уравнения Шр¼дингера (7.2). В результате мы находим выражение

аналогичное (7.4). Однако имеется и существенное различие между выражениями (7.4) и (7.9). В то время как не существует интегрального представления, позволяющего восстановить U(0; x) по U(t; x), выра-

жение (7.9) допускает обращение:

Это связано с различным характером процессов, описываемых уравнениями (7.1) и (7.2). Уравнение диффузии (7.1) описывает диссипативный процесс, ведущий к размыванию со временем локализованных полей, смотри (7.5,7.7). Поэтому уравнение диффузии (7.1) не допускает обращения времени. Уравнение же

Шр¼дингера (7.2) обращение времени допускает: оно инвариантно относительно замены t ! t; ! ?.

Поэтому наряду с прямым выражением (7.9) работает и обратное ему выражение.

A.Преобразование Фурье

Любую функцию f(x), заданную в d-мерном пространстве, можно разложить в интеграл Фурье:

Z

f(x) = dq1dq2 : : : dqd exp(iqx)f~(q); (7.10)

(2 )d

ãäå f~(q) называется преобразованием Фурье функции f(x). Эту величину можно вычислить в соответствии с правилом

Z

f~(q) = dx1dx2 : : : dxd exp( iqx)f(x): (7.11)

Преобразования (7.10) и (7.11) являются обратными друг другу.

Приведем важное соотношение, касающееся так называемой свертки двух функций

Z

h(y) = dx1dx2 : : : dxd f(x)g(y x): (7.12)

Подставляя выражение (7.12) в интеграл Фурье (7.11) и переходя к интегрированию по x и y x, мы находим

Отметим, что для -функции, (x)

(x1) (x2) : : : (xd), преобразованием Фурье явля-

ется единица, ~ = 1. Это свойство является прямым

обобщением соотношений (1.5,1.6). Отметим также обобщение на d-мерный случай соотношения (1.4)

Z

f(y) = dx1dx2 : : : dxd (y x)f(x): (7.14)

Используя теперь соотношения (7.12,7.13), мы возвра-

щаемся к ~

= 1.

B.Задачи

Заметим, что при t ! 0 функция U(t; x) должна переходить в U(0; x). Поэтому из соотношения (7.4) следует

Докажите это соотношение непосредственно.

Найти решение одномерного диффузионного

уравнения для следующего начального условия: U(0; x) = exp[ x2=(2l2)]. Сравните ответ с асимптотическим выражением (7.5).

Найти асимптотическое поведение решения

Найти для уравнения Шр¼дингера асимптотиче- ские выражения, аналогичные (7.5,7.7).

Найти решения одномерного уравнения

Найти аналог представления (7.4) для одномерного поля U(t; x), динамика которое в Фурьепредставлении задается (необратимым) уравне-

8.УРАВНЕНИЯ ХОПФА И БЮРГЕРСА

Уравнением Бюргерса называется уравнение

Уравнение (8.1) получается, например, при исследовании слабо нелинейной одномерной акустической волны в системе отсчета, движущейся с линейной скоростью звука. В этом случае нелинейный по u член в

20

уравнении (8.1) происходит из зависимости скорости звука от амплитуды звуковой волны, а член со второй производной представляет затухание звуковой волны, связанное с диссипацией. Однако область применимости этого уравнения отнюдь не ограничивается приведенным примером, уравнение Бюргерса возникает во многих физических задачах, чем и определяется его значение.

На самых больших временах любое решение уравнения (8.1), стремящееся к нулю на 1 по x, стремит-

ся к нулю, u ! 0. Действительно, в силу уравнения Бюргерса

Таким образом, положительно определенная величи- íà R dx u2 убывает со временем и, при достаточно

большом t, становится сколь угодно малым. Отсюда

и следует приведенное утверждение.

Легко найти асимптотическое по времени поведение решения уравнения Бюргерса u, которое стремится к

нулю при x ! 1. Тогда при больших t значение u становится малым и мы можем пренебречь нели-

нейным членом в уравнении (8.1). В результате мы приходим к чисто диффузионному уравнению. Локализованные решения этого уравнения имеют вид

Более интересным является обратный случай сильной нелинейности, который реализуется, если для на- чальных условий UL 1, где L характерный мас-

штаб (корреляционная длина) начального состояния u(0; x), а U характерное значение поля u(0; x). В

этом случае начальная эволюция поля u может быть

описана в пренебрежении второй производной в уравнении (8.1), когда оно сводится к уравнению

которое называется уравнение Хопфа. Это уравнение содержит только первые производные от u и ли-

нейно по этим производным. Такое уравнение может быть решено методом характеристик (смотри ниже). А именно, можно легко найти уравнения для изменения поля u вдоль специальных траекторий (характе-

ристик):

Таким образом, начальные значения поля u, не меняясь, переносятся со скоростью u. Поле u вследствие