
Truhan-NM-Kinematika
.pdf
20
При решении задач для определения угловых скоростей в плоских механизмах часто применяют метод Виллиса.
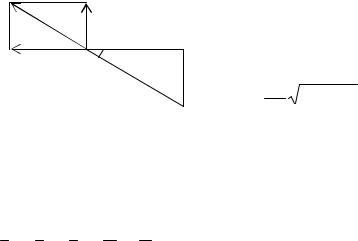
Для этого вводят систему отсчета, неизменно связанную с кривошипом (рис. 9). В этой системе отсчета кривошип
1 |
2 |
.... |
n-1 |
n |
неподвижен, |
а |
|
абсолютные |
|||||||
|
|
|
|
||||
|
|
|
|
|
угловые |
||
|
|
Рис. 9 |
|
|
скорости |
всех |
|
|
|
|
|
колес изменятся |
|||
|
|
|
|
|
на величину |
Ω |
|
угловой скорости кривошипа (относительные угловые
скорости ωir =ωi − Ω).
После этого, рассматривая каждую пару колес, находящихся в зацеплении, можно записать соотношения для скоростей точек соприкосновения, как если бы колеса вращались вокруг неподвижных осей:
ωir ri = ±ω(i+1)r ri+1
или
(ωi −Ω)ri = ±(ωi+1 −Ω)ri+1 ,
где знак “+” ставится в случае внутреннего, а знак “-“ в случае внешнего зацепления между колесами.
Задача 4.1. Решить задачу 2.1, используя формулы кинематики сложного движения точки.
Решение. Движение точек N и M шестерни 4 можно представить как сложное. Подвижную систему отсчета можно выбрать различными способами. Рассмотрим два из них:
1.Система координат вращается с угловой скоростью кривошипа, начало ее помещено в точку О.
2.Система координат движется поступательно, имея начало в точке А.
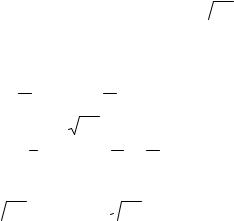
21
Исходя из формул (3.1) и (3.4) проследим, как изменяются при этих выборах подвижной системы отсчета составляющие скорости и ускорения точек M и N.
1. В переносном движении точка M (N) будет двигаться по
окружности радиуса OM = 7r (ON =  37r)с центром в неподвижной точке О, причем
37r)с центром в неподвижной точке О, причем
ωe =ω, εe |
=ε. Значит, |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
veM = vO + |
ω |
e × |
|
|
= |
ωe × |
|
|
|
, |
|
|
|
|
|
|
|
|||||||||
OM |
OM |
|
|
|
||||||||||||||||||||||
veM = 7ωr, (veN = 37ωr), |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
= |
|
+ε |
|
× |
|
+ |
ω |
× |
ω |
× |
|
= |
|
|
вр + |
|
ос , |
|||||||
|
|
|
|
OM |
OM |
|
|
|
||||||||||||||||||
|
W |
W |
e |
W |
|
W |
||||||||||||||||||||
|
eM O |
|
|
|
|
|
|
|
|
e |
|
|
e |
|
|
|
|
eM |
|
eM |
||||||
W вр = 7εr, W ос = 7ω2 r, |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
eM |
|
|
|
|
eM |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
WeN вр =  37εr, WeN ос =
37εr, WeN ос =  37ω2 r.
37ω2 r.
Относительное движение точки M (N) – движение ее вместе с шестерней 4, которая вращается относительно выбранной
подвижной системы с угловым ускорением ε4r и имеет в данный момент угловую скорость ω4r . Для определения ω4r воспользуемся методом Виллиса. Обозначим абсолютные угловые скорости шестерен ω1 = 0, ω2 =ω3 , ω4 . (Это их абсолютные значения).
Перейдем в систему координат, жестко связанную с кривошипом. По отношению к этой системе угловые скорости шестерен будут соответственно:
ω1r =ω, ω2r =ω2 −ω,
ω3r =ω3 −ω, ω4r =ω4 −ω.
Так как проскальзывание в системе отсутствует, то можно приравнивать между собой относительные линейные
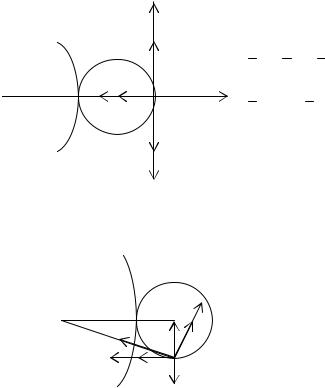
22
скорости точек касания. Учтем теперь, что при внешнем зацеплении шестерни вращаются в противоположных направлениях. Получим
(−ω)r1 = −(ω2 −ω)r2 = −ω2r r2 ,
(ω3 −ω)r3 =ω3r r3 = −(ω4 −ω)r4 = −ω4r r4 ,
откуда ω4r = −4ω. Здесь знак “-“ показывает, что угловая
скорость ω4r |
противоположна угловой скорости кривошипа. |
||||||||||||||||||||||
Так |
как в |
рассматриваемом случае |
система |
совершает |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
плоскопараллельное |
||||||||||||||
|
|
|
|
|
__вр |
|
движение и ωe |
|
|
|
ωr |
|
, то |
||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
We |
|
формула |
|
|
|
|
|
|
|
|
|
|
(4.2) |
|||||
|
|
|
|
|
_ |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
VeM |
|
принимает |
|
|
|
|
|
|
вид |
|||||||||
|
|
|
|
|
|
__ |
ε |
a |
=ε |
e |
+ε |
r . |
|
|
|
|
|
||||||
|
|
__ |
__ |
|
|
Wk |
Таким |
образом, |
зная |
||||||||||||||
|
|
|
|
|
ε |
|
|
|
ε |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Wr n |
Weос |
_ |
|
a |
и |
e , |
находим: |
||||||||||||||
|
|
|
|
|
|
ε4r |
= −4ε . |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
VrM |
|
|
|
|
|
|
|
|
|
|||||||||
|
Рис. 10 |
|
__ |
|
|
|
|
Теперь |
|
можно |
|||||||||||||
|
|
Wrτ |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
найти |
|
|
|
|
|
величины |
||||||||||
относительных скоростей VrM , VrN |
и ускорений WrM , WrN . |
||||||||||||||||||||||
Относительные скорости VrM |
=VrN |
= 4ωr . |
Так |
|
|
|
|
|
|
как |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
__ |
|
|
|
|
относительное |
||||||||||||
__ |
O |
|
|
|
|
WrNвр |
|
движение тела чисто |
|||||||||||||||
WK |
|
|
__ |
|
_ |
|
вращательное, |
|
|
|
то |
||||||||||||
|
|
__ос |
|
|
|
|
|
|
|
|
|
касательная |
|||||||||||
|
|
|
WrNос |
VeN |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
WeN |
|
|
|
|
|
составляющая |
|
|
Wrτ |
||||||||||||
|
|
__вр |
_ |
__ |
|
|
|
|
|||||||||||||||
|
|
|
|
ускорения |
совпадает |
||||||||||||||||||
Рис. 11 |
WrN |
|
VrN |
WK |
|
с |
|
|
|
вращательной |
|||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||

23
Wr вр , а нормальная Wrn - с осестремительной Wr ос :
Wrτ =WrM вр =WrN вр = 4εr, Wrn =WrM ос =WrN ос =16ω2 r
(это не всегда справедливо, так как направления Wrτ и Wrn
определяются траекторией движения точки, а Wr вр и Wr ос
зависят от выбора полюса, с помощью которого записывается выражение ускорения точки тела (см. формулу (2.2)).
Кориолисово ускорение:
WKM = WKN = 2ω4ωr =8ω2 r .
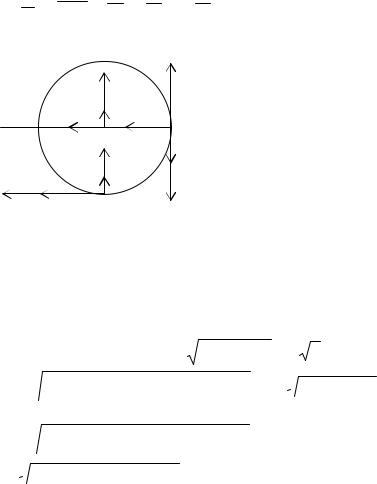
Направления составляющих скоростей и ускорений точек M и N представлены на рис. 10 и 11. Складывая соответствующие составляющие для модулей векторов скорости и ускорения, получаем
VaM =VeM −VrM =3ωr,
V = |
|
6 |
V |
|
|
2 |
|
|
4 |
V |
−V |
|
2 |
|
|
|||
|
37 |
|
|
+ |
|
37 |
|
=3 5ωr, |
||||||||||
aN |
|
|
eN |
|
|
|
|
|
eN |
|
rN |
|
|
|
||||
WaM = (WK −We ос −WrN )2 + (We вр −Wrτ )2 = |
|
|||||||||||||||||
=3r |
ε2 |
+ 25ω4 , |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
6 |
|
W |
вр |
−W |
|
+W |
ос |
|
1 |
+W |
ос |
2 |
||||
|
|
37 |
|
|
|
|
37 |
|
+ |
|||||||||
W = |
|
|
e |
|
|
|
K |
|
e |
|
|
|
r |
|
|
|||
|
W |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||
aN |
|
вр |
|
|
6W ос |
|
|
вр |
|
|
|
|
||||||
|
|
|
e |
− |
|
e |
|
−Wr |
|
|
= |
|
|
|
|
|||
|
+ |
37 |
|
37 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
=3r  13ω4 + 5ε2 +16ω2ε.
13ω4 + 5ε2 +16ω2ε.
24
2. Так как подвижная система координат движется теперь поступательно, то ωe = 0, εe = 0. Поэтому
Ve =VA = 6ωr, We =WA , (WAτ = 6εr, WAn = 6ω2 r).
Относительное движение – движение точки M (N) по окружности радиуса r с центром в точке А. При этом
vr =ω4 × AM , Wr =Wr вр +Wr ос.
|
|
__ |
|
_ |
|
|
|
VeM |
|
|
|
Waτ |
__ |
|
|
|
_ |
|
|
|
|
VA |
WrMос |
_M |
|
|
__ |
|
|
|
|
Wr n |
__ |
VrN |
__вр |
_ |
_ |
WrNос |
|
VrN |
|
__ |
||
WrN |
VrN |
|
WrMвр |
|
|
|
|
N |
|
|
|
|
|
|
|
|
Рис. 12 |
|
|
WKM |
=WKN = 0. |
|
|
|
Относительные угловая скорость и угловое ускорение совпадают в данном случае с абсолютным (см. формулы (4.1) и (4.2)).
Следовательно,
VrM =VrN =3ωr, WrM вр =WrN вр =3εr,
WrN ос =WrN ос =9ω2 r,
Так как система отсчета движется поступательно, то для величины скорости и ускорения точек M и N получаем
(см. рис. 12)
V |
M |
=V |
A |
−V =3ωr, V |
N |
= V 2 |
+V |
2 |
=3 5ωr, |
|
|
rM |
A |
|
rN |
|
WM = 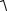 (WAτ −Wr вр )2 + (WAn +Wr ос )2 =3r
(WAτ −Wr вр )2 + (WAn +Wr ос )2 =3r  ε2 + 25ω4 ,
ε2 + 25ω4 ,
WN =  (WAτ +Wr ос )2 + (WAn +Wr вр )2 =
(WAτ +Wr ос )2 + (WAn +Wr вр )2 =
=3r  13ω4 + 5ε2 +16ω2ε.
13ω4 + 5ε2 +16ω2ε.
25
Задача 4.2. Решить задачу 2.2 с помощью формул сложного движения точки.
Решение. Если рассматривать движение диска как сложное, то можно, например, взять в качестве относительного движения вращение диска вокруг оси ОС, а
переносным тогда будет |
вращение диска |
вместе с осью |
|||||
ОС вокруг оси |
OZ. Так как центр диска участвует только в |
||||||
__ |
|
|
переносном |
движении, |
|||
|
|
легко найти переносную |
|||||
ωa |
|
|
|||||
__ |
|
угловую |
|
|
|||
|
ωe R |
|
скорость: |
|
|||
|
C |
ω |
e |
=V / R = at / R. |
|||
__ |
α |
|
|
c |
|
|
|
|
Зная ωe , находим ωr : |
||||||
O |
|
||||||
ωr |
|
r |
|
|
= at |
|
|
|
|
A |
ωa |
R2 + r 2 , |
|||
|
|
|
|
rR |
|
||
Рис. 13 |
|
ωr |
=ωectgα = at / r |
||||
(cм. рис. 13). Соответственно εe |
= a / R , |
εr |
= −a / r , так |
||||
как переносное и относительное движения – вращения вокруг неподвижных в соответствующих системах осей. Абсолютное угловое ускорение получим по формуле (4.2):
ε |
a =ε |
e +ε |
r |
+ |
ωe × |
ωr |
|
a2t 2 |
− |
|
a |
|
|
|
a |
|
|
|
|
+ k |
|||||||||||||
=i |
j |
|
||||||||||||||
rR |
r |
|
R |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Компоненты ускорения точки М найдем по формуле Кориолиса. В проекциях на три ортогональных направления они имеют вид (см.рис.6)

26
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
j |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
вр =ε |
|
|
× |
|
|
|
|
= |
0 |
0 |
|
|
|
a / R |
= |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
OM |
|
|
|||||||||||||||||||||||||||||||||
|
W |
|
e |
|
|
|||||||||||||||||||||||||||||||||||||
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r sin ϕ |
|
|
R |
− r cosϕ |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
a + |
|
ar sin ϕ, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
−i |
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
a2t2 |
|
|
|
|
|
|
|
|
a2t 2 |
|
|
|||||||
|
|
|
|
ос = |
ω |
|
× |
ω |
|
|
|
|
|
|
|
|
|
r sin ϕ − |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
W |
|
e |
e |
×OM = −i |
|
j |
|
|
, |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R2 |
|
|
|
|
|
|
|
|
R |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
j |
|
|
|
|
|||||||||||||
|
|
|
вр =ε |
|
|
× |
|
= |
0 |
|
|
− a / r |
0 |
= |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
CM |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
W |
|
r |
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r sin ϕ |
0 |
|
|
− r cosϕ |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=iacosϕ+ kasin ϕ,
|
|
|
|
ос = |
ω |
|
|
× |
ω |
|
× |
|
= −ω 2 |
|
= |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
CM |
CM |
|
|
|
|
||||||||||||||||||
|
W |
|
r |
r |
|
|
|
|
||||||||||||||||||||||
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
||||||||
= |
a2t2 |
(i |
|
|
|
|
|
|
|
cosϕ), |
|
|
|
|
|
|
|
|||||||||||||
sin ϕ− k |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
j |
k |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
at / R |
= |
||||||||||||||||
|
|
|
|
|
WK = 2 |
ωe ×vr = 2 |
0 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
at cosϕ |
0 |
at sin ϕ |
|
|||||||
|
|
|
|
= |
|
|
2a2t 2 |
cosϕ. |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
j |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||

V. ПРИМЕНЕНИЕ ТЕОРИИ СКОЛЬЗЯЩИХ ВЕКТОРОВ В КИНЕМАТИКЕ
При рассмотрении сложного движения твердого тела требуется найти распределение скоростей точек тела. При этом возникает задача о сложении движений.
Когда говорят о сложении двух вращений или вращательного и поступательного движений тела, то подразумевают, что одно из этих движений тело совершает по отношению к подвижной системе отсчета, а другое – подвижная система отсчета по отношению к неподвижной.
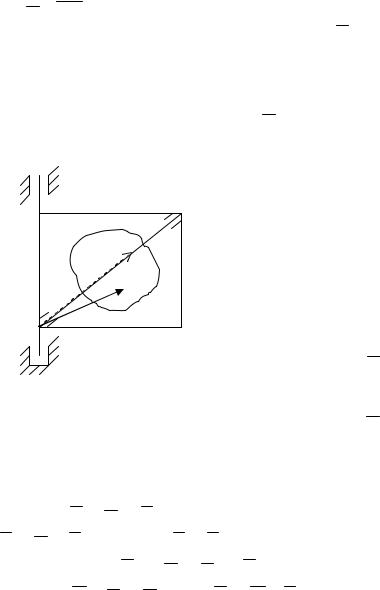
Рассмотрим |
сначала |
сложение |
вращательных |
||||||||
|
|
движений. Покажем, что при этом |
|||||||||
__ |
|
вектор |
ω |
ведет себя как |
скользящий |
||||||
O_ |
вектор, т.е. характеризуется величиной, |
||||||||||
ω |
направлением и линией действия. |
||||||||||
A |
ρ |
|
Пусть |
|
|
тело |
|
совершает |
|||
вращательное |
|
движение |
вокруг |
||||||||
|
i |
|
|||||||||
|
|
некоторой оси. Вектор угловой скорости |
|||||||||
|
|
ω |
задает |
направление вращения и |
|||||||
|
|
скорость изменения угла поворота тела. |
|||||||||
|
|
При |
этом |
распределение |
скоростей |
||||||
|
|
|
|
|
|
|
|
||||
Рис. 14 |
точек тела Vi |
= |
ω |
× ρi |
в силу свойств |
||||||
|
|
векторного произведения не зависит от |
|||||||||
того, в какой точке оси вращения мы построим вектор ω. Момент скользящего вектора относительно полюса О
вводится |
|
|
в |
|
соответствии |
с |
равенством |
||||
mO (F )= |
r |
× |
|
= |
|
× |
|
, где |
|
|
|
|
OA |
OA |
|
|
|||||||
F |
F |
- |
радиус-вектор, |
||||||||
проведенный из полюса О в любую точку А на линии
действия вектора |
F |
. Рассмотрим момент |
вектора |
ω |
||||||||||
относительно полюса О: |
|
|
||||||||||||
mO ( |
ω |
)= |
|
× |
ω |
= |
ω |
× |
|
. |
|
|||
OA |
OA |
(5.1) |
||||||||||||
28
Но - вектор линейной скорости точки О при вращении тела вокруг оси с угловой скоростью ω, т.е.
понятие вектора момента скользящего вектора относительно полюса имеет эквивалент в кинематике в виде вектора линейной скорости полюса О при вращении тела вокруг неподвижной оси. Таким образам, при изучении поля
скоростей точек твердого |
тела |
вектор |
|
ω |
можно считать |
||||
скользящим вектором. |
|
|
|
|
|
|
|
|
|
Рассмотрим теперь распределение |
скоростей |
точек |
|||||||
|
|
твердого тела при других |
|||||||
|
|
движениях |
и покажем, |
||||||
B |
С |
что |
сформулированный |
||||||
|
|
|
|
|
|
|
|
||
__ |
вывод (ω - скользящий |
||||||||
ω1 |
|
вектор) |
сохраняет |
свою |
|||||
_ |
|
силу. |
|
Задача 5.1. |
Тело |
||||
|
|
|
|||||||
Ri |
|
участвует |
в |
двух |
|||||
A |
D |
вращениях |
|
вокруг |
|||||
пересекающихся |
осей, |
||||||||
|
|
т.е. тело вращается с |
|||||||
|
|
угловой |
скоростью |
ω1 |
|||||
Рис. 15 |
|
вокруг некоторой оси АС |
|||||||
|
|
|
|
|
(относительное |
||||
движение), а сама ось вращается с угловой скоростью ω2
вокруг оси АВ, пересекающейся с первой (переносное движение). Найти поле скоростей точек тела.
Решение. Воспользуемся формулой (3.1) сложения скоростей. При этом переносная скорость произвольной
точки тела Ve =ω2 × Ri , относительная скорость
Vr =ω1 × Ri . Подставляя Ve и Vr в (3.1), получаем
Vai = (ω1 +ω2 )× Ri .
Обозначим Ω =ω1 +ω2 . Тогда Vai = Ω× Ri .
29
То есть мы получили, что распределение скоростей точек твердого тела таково, как если бы оно вращалось вокруг оси, направление которой в данный момент определяется
вектором Ω. Таким образом, мы получаем, что угловые скорости, как и любые скользящие векторы с пересекающимися линиями действия, складываются по правилу параллелограмма.
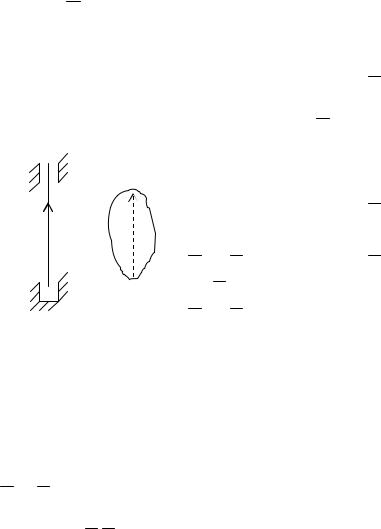
Задача 5.2. Тело вращается с угловой скоростью ω1 вокруг оси 1-1. Ось 1-1 в свою очередь вращается вокруг параллельной ей оси 2-2 с угловой скоростью ω2 . Найти
|
|
|
|
|
|
распределение скоростей точек |
|||||||||||||||
|
|
|
|
|
1 |
тела при следующих условиях: |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
а) направления ω1 и ω2 |
||||||||||||||||
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|||||||||||||||||
__ |
|
|
__ |
совпадают; б) направления |
ω1 |
||||||||||||||||
|
|
|
|
ω1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
ω2 |
|
противоположны |
и |
|||||||||||
ω2 |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||
|
|
2 |
|
|
|
|
|
ω1 |
|
> |
|
|
ω |
2 |
|
; в) направления |
ω1 |
||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
1 |
и |
|
|
ω |
2 |
|
противоположны |
и |
||||||||
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
ω1 |
|
= |
|
|
ω |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
. |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Решение. Вращение тела вокруг оси 1-1 примем за
относительное, а вращение самой оси 1-1 – за переносное. Очевидно, при всех указанных условиях движение
тела будет плоскопараллельным и скорости точек, расположенных на какой-либо прямой, параллельной угловым скоростям, будут в данный момент одинаковы. Поэтому достаточно рассмотреть скорости точек, расположенных в любой плоскости П, перпендикулярной к
ω1 и ω2 .
Случай а). Пусть плоскость П пересекает плоскость (ω1ω2 ) по прямой АВ. Тогда скорость
