Длинные задачи

Тот же результат можно получить более формальным способом, используя третий член в разложении Тэйлора

U ( z0 + ξ) ≈U ( z0 ) +U ′( z0 ) ξ + 21U ′′( z0 ) ξ2 .

То есть, коэффициент κ в уравнении (13) равен второй производной от потенциальной энергии, взятой в точке равновесия.

Подставим полученное выражение в закон сохранения энергии (7) и получим, с учетом Vξ =Vz :

из которого следует, что период колебаний, согласно общей методике, определяется формулой

Проиллюстрируем произошедшие изменения на графике потенциальной кривой - на рисунке: 1- потенциальная

кривая до изменения скорости, E0 -

начальная энергия шайбы. После того, как шайбе сообщили дополнительную скорость изменилась кривая эффективной потенциальной энергии 2 и увеличилась энергия шайбы E . Для наглядности рисунка мы увеличили скорость шайбы в полтора раза.

4. По-прежнему, при движении шайбы в горизонтальной плоскости ее скорость определяется выражением V0 = gz0 . Если шайбе сообщить дополнительное приращение скорости v , направленное вдоль боковой

21

Таким образом, пределы изменения вертикальной координаты определяются выражениями:

Обратите внимание, что в данном случае точка z0 является точкой равновесия, об этом свидетельствует отсутствие линейного по ξ слагаемого в выражении для

эффективной потенциальной энергии. Заметим также, что пределы изменения вертикальной координаты не зависят от того, как направлено изменение скорости «вверх» или «вниз».

Подставим упрощенное выражение для эффективной потенциальной энергии в уравнение (17), получим

Из этого уравнения следует, что период колебаний вдоль вертикальной оси в этом случае определяется по формуле

Дадим графическую иллюстрацию и в этом случае. Так как эффективная потенциальная энергия определяется только радиальной составляющей скорости, то она осталась неизменной. Изменилась только полная энергия шайбы. Как и в предыдущем случае, приращение скорости в два раза меньше скорости начальной. Заметьте, что изменение полной энергии в данном случае меньше.

23

Для закрепления методики решения задач такого типа рекомендую самостоятельно решить практически аналогичную задачу.

Военный космический корабль движется с выключенными двигателями по круговой орбите на высоте h = 600км над поверхностью Земли. На корабле установлена пушка, которая может выпускать снаряды со скоростью v0 = 800м / с относительно корабля. Масса снаряда значительно меньше массы корабля.

1. Снаряд выстрелили в направлении движении корабля.

а) На какое максимальное расстояние от поверхности Земли удалится снаряд? б) Найдите период обращения снаряда вокруг Земли.

2. Снаряд выстреливают в направлении противоположном центру Земли.

а) Найдите максимальное и минимальное удаление снаряда от поверхности Земли. б) Чему равен период обращения снаряда в этом случае?

в) При каких начальных скоростях снаряда относительно корабля снаряд сможет упасть на Землю?

Задача 5. «Оборотный маятник»

Оборотный маятник представляет собой тонкий однородный стержень длиной l , по которому можно перемещать две одинаковых массивных чечевицы A1 и A2 . Положение чечевиц определяется координатами x1 и x2 .

Маятник может колебаться в вертикальной плоскости, будучи подвешенным на упорах S1 или S2 (в этом случае его необходимо перевернуть). Масса

стержня значительно меньше массы чечевиц. Чечевицы можно считать материальными точками. Расстояния от упоров до концов стержня одинаковы и равны a .

1. Найдите периоды колебаний маятника в прямом(на упоре S1 ) и обратном (на упоре S2 )

положениях в зависимости от x1 и x2 .

2. Постройте график зависимости периода колебаний маятника в прямом положении при

x1 = a2 от положения второй чечевицы.

3. Найдите множество значений x1 , x2 , при которых период колебаний маятника T1 в прямом

положении один и тот же. Постройте эти множества точек на диаграмме( x1 ,x2 ) для

различных значений T1 . Постройте аналогичные кривые для колебаний маятника в обратном положении.

24

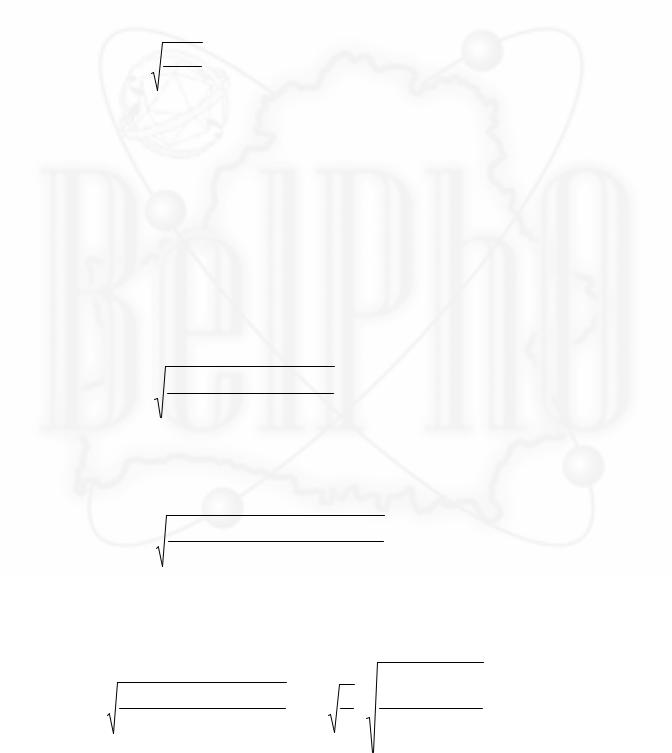
4. На диаграмме ( x1 ,x2 ) постройте множество значений ( x1 , x2 ), при

которых периоды колебаний маятника в прямом и обратном положениях равны и постоянны. Покажите, что этот период равен периоду колебаний математического маятника с длиной равной расстоянию между упорами.

Решение.

1. Воспользуемся известной формулой для периода колебаний физического маятника

где M - масса маятника, I - момент инерции маятника относительно оси вращения, b - расстояние от оси вращения до центра масс маятника. Момент инерции маятника в прямом положении рассчитывается по формуле

здесь m- масса одной чечевицы. Расстояние от центра масс до оси вращения вычисляется по формуле

Таким образом, период колебаний математического маятника в прямом положении выражается формулой (учитывая, что масса маятника M = 2m)

Формула для периода колебаний в обратном положении может быть

График этой функции удобно строить в следующих координатах: по горизонтали - отношение x2 / a ; по вертикали

проанализировать и построить график этой функции можно по известным методикам.

Результат построения представлен на рисунке.

3. Из формулы (4) следует, что множество точек ( x1 ,x2 ), для которых период колебаний T1 постоянен удовлетворяет уравнению

увеличению параметра p . Легко заметить, что все окружности семейства (8) проходят через точку x1 = x2 = a , как бы «вырастают из нее»- рисунок а).

Семейство точек, удовлетворяющих условию T2 = const , можно получить из рассмотренного семейства тем же , что и ранее преобразованием

и описывать окружности, «произрастающие из точки» x1 = x2 = l − a , см. рисунок б).

26

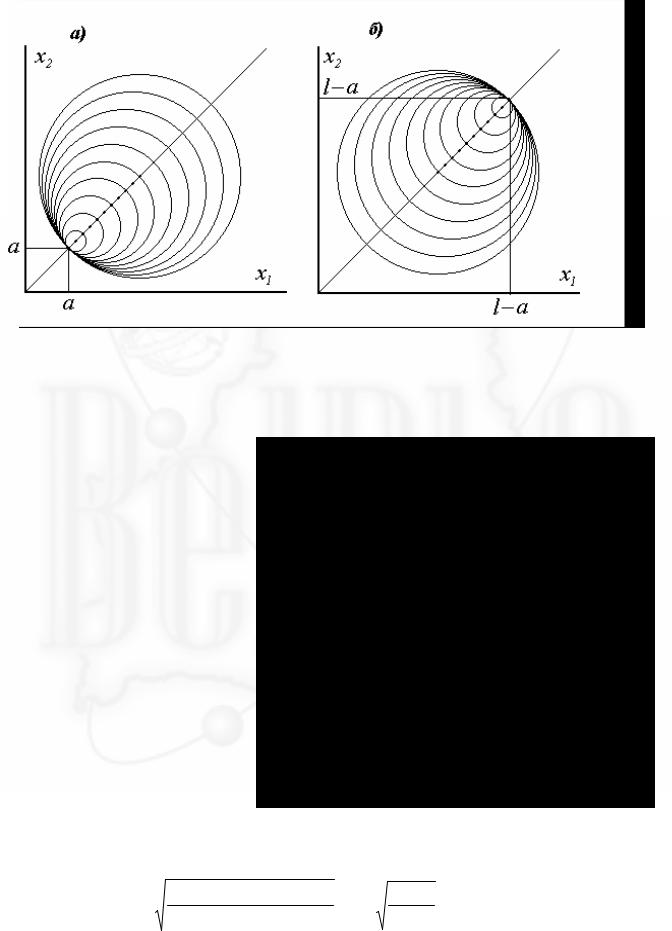
4. Для того, что бы определить множество точек для которых периоды колебаний в прямом и обратном положении были одинаковы, необходимо найти окружность, которая принадлежит обоим семействам. Такой линией является окружность, проходящая через точки x1 = x2 = a и x1 = x2 = l − a .

На рисунке она выделена как более жирная.

Уравнение этой окружности имеет вид

Период колебаний в этом случае можно рассчитать по формуле (4) положив в ней x1 = x2 = l − a :

К аналогичному результату приводит применение формулы (5), если положить в ней x1 = x2 = a . Формула (11) описывает также период колебаний

математического маятника с длиной равной расстоянию между упорами.

27

Замечания.

Оборотный маятник, описанный в данной задаче таже носит имя маятника Бесселя. Он достаточно широко применяется для точного измерения ускорения свободного падения. Суть таких измерений сводится к определению такого периода колебаний, который был бы одинаков как в прямом, так и в обратном положениях, и последующем применении формулы (11).

Сначала можно построить график

заметить, что дополнительное слагаемое неотрицательно и обращается в нуль на концах рассматриваемого интервала (кривая 2). Немного выше будет лежать график функции

в которой дополнительное слагаемое также неотрицательно и обращается в нуль на концах рассматриваемого интервала (кривая 3). На представленом рисунке эти функции построены с помощью компьютера точно. Конечно, физический смысл имеет область только положительных значений параметра µ . Таким образом, область допустимых

значений рассматриваемых параметров разбивается на четыре части:

-в области I выполняется неравенство (6), то есть шайба успеет проскочить «вперед» до тех пор, пока ее догонит вращающийся стержень;

-в области II выполняется неравенство (5), следовательно, шайба будет двигаться «вперед», но не выполняется (6), поэтому стержень успеет ее догнать;

-в области III выпоняется неравенство (7), следовательно, относительно центра стержня шайба будет двигаться «назад» и испытает столкновение со стержнем, так как не выполняется неравенство (8);

-наконец, в области IV выполняется неравенство (8), следовательно, шайба отразится «назад», не испытав второго столкновения со стержнем.

3. Если после первого удара скорости шайбы и центра стержня окажутся равными, то в системе отсчета, связанной с центром стержня, второй удар произойдет в той же точке (обозначенной буквой C на предыдущих рисунках), что и первый. Поэтому после него восстановятся характеристики движения, существовавшие до первого удара. Следовательно, для того чтобы после второго удара шайба двигалась с прежней скорость необходимо выполнения условия v1 = u , что достигается при

28

4. Необходимо заметить, что при заданных значениях параметров, после первого удара скорости шайбы и центра стержня оказываются весьма близки. Действительно, подсчет по формулам (4) показывает, что

считать, что после удара шайба востановит свою первоначальную скорость v0′ = v0 − u (не забывайте - мы

работаем в системе отсчета, связанной с центром стержня!) , но направлена она будет перпендикулярно стержню в момент удара. Следовательно, после второго удара шайба преобретет малую компоненту скорости, перпендикулярную первоначальному направлению и равную

v = ( v0 − u )α = v0 12ξ2 −1 + µα ≈1,96 10−4 v0 . 12ξ2 + 1 + µ

Изменение компоненты скорости, параллельной первоначальному направлению мало, поэтому направление скорости изменится на малый угол

β= v ≈ 2,0 10−4 . v0

29

Задача 6. «Упругая цепочка»

Бесконечная цепочка состоит из одинаковых шариков (масса каждого m), соединенных одинаковыми легкими пружинами (жесткость каждой γ ). В

положении равновесия расстояния между шариками равны l , пружины немного растянуты так, что сила натяжения каждой равна T0 .

Часть 1. Продольные волны.

Допустим, что каждый шарик может двигаться только в направлении вдоль цепочки.

1.1 Найдите собственную частоту колебаний одного из шариков ω0 , если два соседних закреплены.

1.2По цепочке распространяется продольная волна. Найдите сдвиг фаз между колебаниями двух соседних шариков при частоте волн ω .

1.3При каких частотах колебаний ω по цепочке могут распространяться бегущие волны?

1.4Найдите скорость распространения продольной волны по цепочке. Постройте примерный график этой зависимости.

1.5Найдите скорость распространения продольной волны при частотах

ω<< ω0 . Покажите, что полученное выражение можно считать аналогом

ρ- плотность среды.

1.6В цепочке неподвижно закрепили неподвижно два шарика так, что между ними оказалось n шариков. Определите все частоты собственных колебаний этого участка цепочки, соответствующие различным модам стоячих волн.

Часть 2. Поперечные волны.

Пусть шарики способны перемещаться только в направлении перпендикулярном цепочке, причем их смещения малы ( ∆x << l ) .

30