
Vse_bomby_s_dokazatelstvami
.pdf
13. Степенные ряды. Радиус сходимости.
Определение. Функциональный ряд
где an и z0 - комплексные числа, а z - комплексная переменная, называется степенным рядом.
Определение. Радиусом сходимости степенного ряда (1) называется число
или 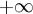 :
: кругом сходимости ряда (1) называется круг
кругом сходимости ряда (1) называется круг
Круг сходимости является открытым множеством. При 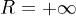 он совпадает со всей комплексной плоскостью.
он совпадает со всей комплексной плоскостью.
Формула (2) называется формулой Коши-Адамара.
Теорема. Признак Коши. Пусть в  . Тогда
. Тогда
1.при l < 1 ряд сходится
2.при l > 1 ряд расходится и даже общий член не стремиться к нулю.
Теорема. Пусть R - радиус сходимости ряда. Тогда
1.при | z | < R ряд сходится и даже абсолютно.
2.при | z | > R ряд расходится и даже общий член не стремится к нулю. Теорема. Пусть R - радиус сходимости степенного ряда, 0 < r < R. Тогда в круге 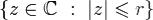 ряд сходится равномерно.
ряд сходится равномерно.
Доказательство: 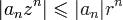 - числовой сходящийся ряд.
- числовой сходящийся ряд.
Бесконечная дифференцируемость суммы степенного ряда.
Пусть R > 0 - радиус сходимости ряда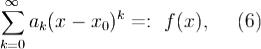
ak - вещественные числа.Тогда при | x − x0 | < R f имеет производные всех порядков, которые находятся почленным дифференцированием; Доказательство.Докажем утверждение, что степенные ряды, полученные почленным дифференцированием или почленным интегрированием, имеют тот же радиус сходимости R.
Радиусы сходимости рядов  и
и 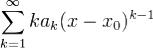 совпадают.
совпадают.
Доказательство. Пусть радиусы сходимости указанных рядов соответственно R и R'. Очевидно, что ряд  сходится там же, где
сходится там же, где 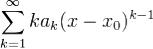 , и, следовательно, имеет тот же радиус сходимости R'.
, и, следовательно, имеет тот же радиус сходимости R'.
В силу Утверждение следует из 3 и равномерной сходимости ряда.
Утверждение следует из 3 и равномерной сходимости ряда.
Ряд Тейлора.
Если функция 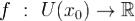 определена в некоторой окрестности точки
определена в некоторой окрестности точки  и имеет в точке x0производные всех порядков (т.е. является бесконечно дифференцируемой в точке x0), то степенной ряд
и имеет в точке x0производные всех порядков (т.е. является бесконечно дифференцируемой в точке x0), то степенной ряд
 называется рядом Тейлора функции f в точке x0.
называется рядом Тейлора функции f в точке x0.

14. Формула Грина.
Пусть функции P(x,y) и Q(x,y) непрерывно дифференцируемы в односвязной области  , а простой кусочно гладкий контур
, а простой кусочно гладкий контур 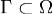 ограничивает область
ограничивает область 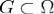 . Тогда справедлива формула Грина
. Тогда справедлива формула Грина
где  есть положительно ориентированная граница области G.
есть положительно ориентированная граница области G.
Доказательство.
Докажем сначала формулу (1) в наиболее простом случае, когда
область G еще и элементарна относительно обеих координатных осей, т.е. существуют такие кусочно непрерывно дифференцируемые и непрерывные функции  , и
, и 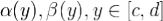 , что
, что
 .
.
Примерами таких областей явл внутренности круга, эллипса, треугольника. Применяя формулу сведения двойного интеграла к повторному, получаем
Добавленные интегралы по вертикальным отрезкам DE и NA равны нулю, так как на этих отрезках x = const. Аналогично доказывается формула
Складывая равенства (2) и (3) получаем формулу Грина (1).
Пусть теперь область G по-прежнему ограничена кусочно гладкой замкнутой кривой 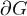 . Предположим её можно кусочно гладкой простой кривой Γ разбить на две области простейшего вида рассмотренные выше. Тогда
. Предположим её можно кусочно гладкой простой кривой Γ разбить на две области простейшего вида рассмотренные выше. Тогда ,
,
Применяя формулу Грина в каждой из областей G1 и G2, получаем при складывание, что интегралы по Γ и Γ− взаимно уничтожается и мы опять приходим к формуле Грина. При помощи математической индукции легко обобщить на случай односвязной области.
Потенциальные векторные поля на плоскости.
Векторное поле 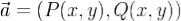 , заданное на области
, заданное на области 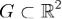 , называется потенциальным в области G, если существует непрерывно
, называется потенциальным в области G, если существует непрерывно
дифференцируемая функция 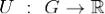 такая, что
такая, что на G. Функцию U называют при этом потенциальной функцией поля
на G. Функцию U называют при этом потенциальной функцией поля 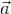 или потенциалом поля
или потенциалом поля 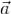 .
.

15.Формула Остроградского-Гаусса.
Пусть  - ограниченная область, граница которой
- ограниченная область, граница которой 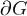 есть кусочно гладкая поверхность, ориентированная внешними нормалями.
есть кусочно гладкая поверхность, ориентированная внешними нормалями.
В  задано непрерывно дифференцируемое векторное поле
задано непрерывно дифференцируемое векторное поле  . Тогда поток векторного поля
. Тогда поток векторного поля 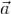 через границу области
через границу области 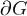 равен тройному интегралу от
равен тройному интегралу от 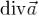 по области G, т.е.
по области G, т.е.
 , или
, или
Доказательство.Докажем сначала формулу Остроградского-Гаусса в одном важном частном случае, когда область G еще и элементарна относительно всех трех координатных осей. Напомним, что область G называется элементарной относительно оси z, если найдутся две такие непрерывные в замыкании области  функции
функции  и ψ(x,y), что
и ψ(x,y), что 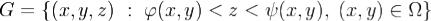 .
.
Применяя формулу сведения тройного интеграла к повторному, получаем
 .(3) Здесь Σ1 - поверхность, являющаяся графиком функции ψ(x,y), a Σ2 - поверхность, являющаяся графиком функции
.(3) Здесь Σ1 - поверхность, являющаяся графиком функции ψ(x,y), a Σ2 - поверхность, являющаяся графиком функции  .
.
Соленоидальные векторные поля.
Кусочно гладкую поверхность, являющуюся границей ограниченной односвязной области, в дальнейшем для краткости будем называть допустимой.Непрерывно дифференцируемое в области G поле  будем называть соленоидальным, если поток вектора
будем называть соленоидальным, если поток вектора  через любую допустимую поверхность
через любую допустимую поверхность 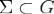 равен нулю.
равен нулю.

16.Формула Стокса для простой гладкой поверхности.
Пусть в ориентированном евклидовом пространстве задана простая поверхность Σ уравнением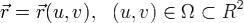 .(1)
.(1)
Здесь Ω - замкнутая область, граница которой есть положительно ориентированный гладкий (или кусочно гладкий) контур (при обходе границы  область Ω остается слева). Пусть
область Ω остается слева). Пусть  задается уравнениями
задается уравнениями 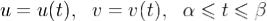 .(2)
.(2)
Образ кривой  при отображении (1) мы назвали положительно ориентированным краем поверхности Σ и обозначили
при отображении (1) мы назвали положительно ориентированным краем поверхности Σ и обозначили  . Напомним, что ориентация поверхности Σ, создаваемаяя полем нормалей
. Напомним, что ориентация поверхности Σ, создаваемаяя полем нормалей 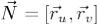 , называется согласованной с положительной
, называется согласованной с положительной
ориентацией края. Было показано, что такое согласование совпадает с известным правилом правого винта.
Пусть в окрестности поверхности Σ задано непрерывно дифференцируемое векторное поле 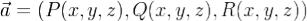 . Если γ - замкнутый
. Если γ - замкнутый
контур, то криволинейный интеграл 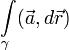 в физике называют циркуляцией векторного поля
в физике называют циркуляцией векторного поля 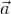 по контуру γ. Если
по контуру γ. Если  , то говорят, что поверхность Σ натянута на контур γ.
, то говорят, что поверхность Σ натянута на контур γ.
Теорема Стокса.Циркуляция векторного поля по контуру
по контуру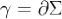 равна потоку вихря этого поля через поверхность Σ, натянутую на контур γ, т.е.
равна потоку вихря этого поля через поверхность Σ, натянутую на контур γ, т.е.
Доказательство.Докажем теорему Стокса в тех предположениях, которые были сформулированы в начале. Из (1) и (2) получаем уравнение края поверхности .
.
Сводя криволинейные интегралы к определенным, получаем
 .
.

Сделаем дополнительное предположение о непрерывности (а следовательно и равенстве) смешанных производных 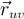 и
и  . Тогда в силу формулы Грина получаем равенство
. Тогда в силу формулы Грина получаем равенство
 .
.
Здесь была использована формула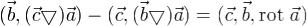 при
при 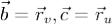 , а также формула, выражающая поток через двойной
, а также формула, выражающая поток через двойной
интеграл от смешанного произведения: . Итак, формула Стокса доказана для простой гладкой поверхности, натянутой на кусочно глакий контур.
. Итак, формула Стокса доказана для простой гладкой поверхности, натянутой на кусочно глакий контур.

17. Теорема о сходимости ряда Фурье в точке.f - 2π периодическая, абсолютно интегрируемая на[ − π,π] функция.x0 – еёпочти регулярная
точка f.Тогдаряд Фурье в этой точкеx0 сходится к . Если же при этом x0 - регулярная точка f, то ряд Фурье в точке x0 сходится
. Если же при этом x0 - регулярная точка f, то ряд Фурье в точке x0 сходится
к f(x0).Рассмотрим предел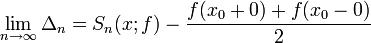
Дробь  , доопределенная единицей в нуле, является непрерывной на [
, доопределенная единицей в нуле, является непрерывной на [
− π,π] функцией.Дробь 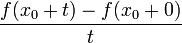 абсолютно интегрируема на [ − π,π] функция, поскольку таковой является её числитель, и при
абсолютно интегрируема на [ − π,π] функция, поскольку таковой является её числитель, и при 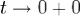 она имеет конечный предел.По теореме Римана об осцилляции, последний интеграл стремиться к нулю при
она имеет конечный предел.По теореме Римана об осцилляции, последний интеграл стремиться к нулю при  , т.е.
, т.е.
 при
при 
Следствие.Пусть 2π - периодическая функция f абсолютно интегрируема на отрезке [ − π,π], и существуетf'(x0). Тогда ряд Фурье функции f сх. в x0 к f(x0).

18. Дост. условия равномернойсх-сти тригонометрического ряда Фурье.
Пусть f - 2π периодическя и кусочно непрерывно дифференцируемая функция.Тогда ряд Фурье функции f сходится к f равномерно на 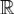 и
и
 при
при 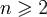 ,где C не зависит от n. Доказательство. Пусть 0 < δ = δn < π. Перепишем формулу
,где C не зависит от n. Доказательство. Пусть 0 < δ = δn < π. Перепишем формулу
в виде
 .
.
Пусть M1 = max | f' | . C помощью теоремы Лагранжа о конечных приращениях получаем, что при 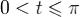
 .Следовательно, при
.Следовательно, при 
и (за исключением быть может, конечного числа
значений t)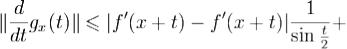
 .
.
Очевидно, что  .С помощью интегрирования по частям имеем
.С помощью интегрирования по частям имеем
 . Отсюда
. Отсюда . Пологая
. Пологая 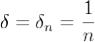 , получаем, что при
, получаем, что при 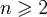
,где C не зависит от n. Доказана.

19. Преобразование Фурье абсолютно интегрируемой на  функции есть ограниченная и непрерывная на
функции есть ограниченная и непрерывная на  функция.
функция.
Доказательство. Так как функция f(x) абсолютно интегрируема на 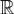 , то
, то
и, следовательно, 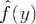 есть ограниченная функция на
есть ограниченная функция на 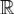 .
.
Для доказательства непрерывности функции  запишем её в виде
запишем её в виде
и заметим, что, в силу леммы 4, $74 функция a(y) и b(y) непрерывны на 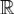 . Лемма 4.Если f(x) - абсолютно интегрируемая на
. Лемма 4.Если f(x) - абсолютно интегрируемая на  функция, то
функция, то
функции a(y) и b(y), определенные равенствами
Доказательство. Докажем, например, непрерывность a(y). Из уравнения для a(y) следует, что
Так как функция f(t) абсолютно интегрируема, то интервал  можно разбить на три таких интервала
можно разбить на три таких интервала  и
и 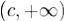 , что по бесконечным интервалам интегралы от функции |f(x) | не будут
, что по бесконечным интервалам интегралы от функции |f(x) | не будут
превышать 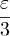 . второй итнеграл меньше чем
. второй итнеграл меньше чем ,
,
и, следовательно, существует δ > 0 такое, что при | Δy | < δ второй интеграл
меньше 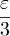 . Следует, что при | Δy | < δ приращение
. Следует, что при | Δy | < δ приращение  .
.
Преобр Фурье производной и производная преобразования Фурье.
Если непрерывная и абсолютно интегрируемая на 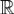 функция f(x) является кусочно гладкой на любом отрезке
функция f(x) является кусочно гладкой на любом отрезке  , а функция
, а функция  абсолютно интегрируема на
абсолютно интегрируема на 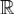 , то
, то .
.
