Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный физико-технический университет (МФТИ)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Трухан. Динамика твердого тела

.pdf

Скачиваний:

Добавлен:

03.06.2015

Размер:

733.35 Кб

Скачать

☆

<<< < Предыдущая 12 / 52 3 4 5 > Следующая >>>

OXY,

центральные моменты инерции A, B, C. Построить главные

оси	инерции	тела	для	точки O	с координатами
ξO = a, ηO = b, ζO = O.
	Решение. В точке O построим систему координат
OXYZ с осями,		параллельными главным центральным осям.
Так	как точка	O	лежит	в плоскости,	содержащей две

главные центральные оси, то по выводу 4 из задачи 1.1 ось OZ - главная для точки O. Значит нужно найти только две главные оси.

Пусть некоторая ось u лежит в плоскости проходит через точку O и образует с осью OX угол α. Тогда направляющие косинусы оси u в системе OXYZ будут равны соответственно cosα, sinα, 0. Момент инерции тела относительно оси u приобретает вид

Ju = J x cos2 α + J y sin2 α −2J xy sinα cosα. (1.19)

Так как в данном случае

cos2 α +cos2 β +cos2 γ = cos2 α +sin2 α =1

независимо от значения угла α, то для отыскания

направления главной оси нет необходимости рассматривать задачу на условный экстремум, и направление главной оси

можно найти из условия стационарности функции Ju :

		dJu		= 0.			(1.20)
Что дает		dα		= 0.			(1.20)
		dα

− J x sin 2α + J y sin 2α −2J xy cos 2α = 0.
Откуда	1				2Jxy
α =	1		arctg		2Jxy		.
α =	2		arctg		J y	− Jx	.
	2				J y	− Jx

Но из задачи 1.1 следует

J x = A +mb2 , J y = B + ma2 , Jxy = mab.

			12
И, значит,	1		2mab
α =
		arctg	B − A +m(a2 −b2 )	.	(1.21)
	2

Таким образом, повернув ось OX вокруг точки O на угол α, определяемый равенством (1.21), мы совместим ее с

главной осью. Момент инерции относительно построенной главной оси может быть найден в результате подстановки α из равенства (1.21) в выражение (1.19).

§ 2. Подсчет основных динамических величин для твердого тела с одной неподвижной точкой

2.1. Кинетический момент. В каждый момент времени твердое тело с неподвижной точкой О имеет такое

же распределение скоростей Vi точек, как при вращении

вокруг неподвижной оси, т.е.
вокруг неподвижной оси, т.е.	Vi		=	ω	×	ri	, где	ω	- вектор
мгновенной угловой скорости,	ri	- радиус-вектор i -й точки,

проведенный из неподвижной точки. Поэтому кинетический момент тела относительно точки О будет

KO = ∑miri ×Vi = ∑miri ×(ω ×ri )

или с помощью тензора инерции J KO = Jω.

Если тензор инерции J записан в системе осей, главных для точки О, то он имеет диагональный вид. Вектор угловой

скорости в этих осях

= pi

+qj

+rk ,

и вектор

кинетического момента

O = Api

+ Bqj

+Crk

(2.1)

( A, B, C - осевые моменты инерции). Векторы ω и KO , вообще говоря, не коллинеарны. Они, очевидно, совпадают

по направлению лишь в том случае, если ось вращения совпадает с главной осью. При этом KO = Jω = λω , где λ является коэффициентом пропорциональности. И, значит, J −λEω = 0. Условие нетривиальности решения этого

уравнения: detJik −λδik = 0. Отсюда следует, что

собственные векторы матрицы J определяют направления главных осей инерции, а собственные значения этой матрицы

– моменты инерции относительно главных осей.

2.2. Кинетическая энергия.							Кинетическая энергия
T =	1	∑miVi	2	=	1	∑mihi		2ω2 =	1	JOωω2. (2.2)
	2				2				2

Здесь JOω = ∑mihi2 - момент инерции тела относительно мгновенной оси вращения, hi - расстояние i-й точки от этой оси.

По теореме Гюйгенса-Штейнера JOω = JM ω +md 2

(d - расстояние между мгновенной осью вращения и осью, проходящей через центр масс параллельно мгновенной,

JM ω - момент инерции тела относительно последней).

Выражение кинетической энергии можно представить в форме

T = 12 md 2ω2 + 12 JM ωω2 = 12 mVM 2 + 12 J M ωω2 , (2.2)

где VM - скорость центра масс тела. Формула (2.2)

представляет собой аналитическое выражение теоремы Кенига для твердого тела. Обратим внимание, что кинетическая энергия относительного движения

T '=	1	JM ωω2	есть кинетическая энергия вращательного
	2

движения вокруг оси, проходящей через центр масс

параллельно мгновенной.

Выражение

(2.2)

кинетической

энергии

осях

Oξηζ , главных для

неподвижной

точки,

записывается в

виде

(Ap2 + Bq2

+Cr 2 ).

T =

(2.3)

Аналогично формула (2.2) в главных центральных

осях может быть представлена так:

2 ).

T =

mVM

(AM pM

2 + BM qM

+CM rM

(2.4)

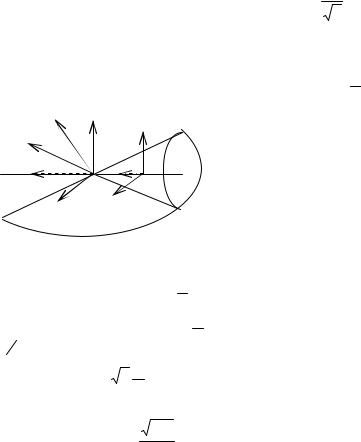
Задача 2.1. Однородный круговой конус массы m с

высотой h и углом при вершине 60D катится без проскальзывания по неподвижному конусу с углом при

вершине 120D (см. рис. 2.1). Найти величину вектора кинетического момента KO и угол β, который образует этот

вектор с вектором ω. Подсчитать кинетическую энергию T конуса, если центр его основания движется с постоянной по величине скоростью V.

Решение. Величину вектора KO найдем с помощью равенства

KO =

O 60o O1

120o

A2 p2 + B2q2 +C 2r 2 . (2.5)

Так как центральный эллипсоид инерции – эллипсоид вращения, а точка O лежит на главной центральной

оси, то главные оси для этой точки получаются

параллельным переносом главных

Рис. 2.1

центральных осей MξMηMζM .

Центр масс однородного

кругового конуса лежит на расстоянии

h от его вершины,

т.е. OM =

h. Главные

центральные моменты

инерции

конуса равны

mR2 , где R = h

AM = BM =

m(4R2 +h2 ), CM

радиус

основания

конуса.

Таким

образом,

A = B = AM

+mOM 2

mh2

C =CM =

mh2.

Вектор

угловой

скорости

направлен

по

Ko η

ηM

мгновенной

оси

вращения,

ζM M

совпадающей с линией

касания

подвижного и

неподвижного конусов.

ξM

Центр

основания

конуса

движется

со

Рис. 2.2

скоростью

находится

от

мгновенной оси на расстоянии h2 , поэтому угловая скорость

ω =

. Проекции вектора

на оси системы Oξηζ :

h 2

p = 0,

q =

r =

3 V

. Подставляя в (2.5) найденные

значения моментов инерции и компонентов вектора угловой

скорости, получим KO =	181 mVh. Вектор		O образует с
		K
	20

												16
осью			Oζ				угол				α = arctg					Bq	= arctg			13 .	Откуда
																Cr				2 3
β =		30D −α			.						T
			Для подсчета								T	воспользуемся							формулой (2.3).
Используя найденные при подсчете																	KO значения				A, B, C и
p, q, r, получим
	1		13			2 V		2		1		2 3V			2		19		2
T =	1		13	mh		2 V				1	mh	2 3V					19	mV	2
									+							=				.
	2		20				h	2	+	10			h	2		=	40			.
	2		20				h			10			h				40

§ 3. Уравнения движения тела с неподвижной точкой. Случай Эйлера и случай Лагранжа

3.1. Уравнения движения. Твердое тело с одной неподвижной точкой имеет три степени свободы.

Часто в качестве координат, однозначно задающих положение твердого тела с неподвижной точкой, берут углы Эйлера: ψ - угол

ζ	Z		прецессии,				θ	-	угол
_.	_._	η	нутации,			ϕ		-	угол
ϕ	θ ψ		собственного					вращения
	_	Y	(см. рис. 3.1). Эти углы
			и	их		производные
ψ	θ.		связаны с				проекциями
	ϕ		вектора					угловой
X	ξ		скорости		ω		на главные
			оси	кинематическими

	Рис. 3.1		соотношениями Эйлера:
	p =ψ sinθ sin ϕ+θ cosϕ
	q =ψ sinθ cos ϕ−θ sin ϕ								(3.1)

r =ψ cosθ +ϕ.

Уравнения динамики тела с одной неподвижной точкой получим с помощью теоремы об изменении кинетического момента

(3.2)

Запишем вектор

O в проекциях на

главные

оси,

построенные для неподвижной точки

O = Api

+ Bqj

+Crk

Так как система главных осей подвижная и жестко

связана с телом, то

×k

×i

Обозначим

= Api

+ Bqj +Crk

. Тогда

теорему

об

изменении кинетического момента можно записать в форме

d' KO

O =

O .

(3.3)

Здесь

- изменение вектора KO

относительно

выбранной подвижной системы координат (иначе относительная скорость конца вектора KO ), а ω ×KO -

изменение вектора KO за счет движения подвижной системы координат (переносная скорость конца вектора KO ). Таким образом, движение конца вектора KO рассматривается как

сложное: вместе с подвижной системой координат, жестко связанной с телом и относительно нее.

Проецируя равенство (3.3) на главные оси, построенные для неподвижной точки, получаем динамические уравнения Эйлера:

Ap +(C − B)qr = Mξ

18
Bq +(A −C)pr = Mη	(3.4)
Cr +(B − A)qp = Mζ .

Уравнения (3.4) совместно с уравнениями (3.1) описывают движение тела с неподвижной точкой и записываются в подвижных осях, жестко связанных с телом, главных для неподвижной точки.

Общее решение системы (3.4) и (3.1) позволяет в каждый момент найти значения углов Эйлера, однозначно задающих положение тела с неподвижной точкой, т.е.

ψ =ψ(t,C1,...,C6 ),

θ =θ(t,C1,...,C6 ), (3.5) ϕ = ϕ(t,C1 ,...,C6 ).

Известно, что лишь в трех случаях при произвольных начальных условиях интегрирование системы уравнений Эйлера может быть доведено до квадратур. Это случаи Эйлера, Лагранжа и Ковалевской. Здесь будет рассмотрено решение задач в случаях Эйлера и Лагранжа.

3.2. Случай Эйлера. Этот случай соответствует движению по инерции, когда MO = 0.

Тогда при произвольной форме тела сохраняется вектор кинетического момента KO и кинетическая энергия

T. Интегрирование системы динамических уравнений Эйлера может быть доведено до квадратур, которые получаются в виде эллиптических интегралов. При некоторых начальных условиях эти квадратуры вырождаются в обыкновенные интегралы, и тогда p, q, r

являются гиперболическими функциями времени.

Задача решена до конца, если найдена зависимость эйлеровых углов от времени.

Так как KO = const, возьмем неподвижную ось OZ

вдоль вектора кинетического момента. Тогда

Ap = KO sinθ sin ϕ,

Bq = KO sinθ cosϕ,

Cr = KO cosθ.

Из (3.6) находим	Cr(t),
cosθ =	Cr(t),
	KO
tg ϕ =	Ap(t)
tg ϕ =	Bq(t).

(3.6)

(3.7)

(3.8)

Чтобы найти ψ, умножим				первое из уравнений (3.1) на
sin ϕ, а второе – на cos ϕ и сложим
	psin ϕ+ q cosϕ =ψ sinθ.
Откуда			psin ϕ+ q cosϕ
	ψ =		psin ϕ+ q cosϕ					.
	ψ =							.
				sinθ
Используя (3.7) и (3.8), найдем выражения
	sinθ =	1		A2 p2 + B2q2 ,
	Ap		KO					Bq
sin ϕ =	Ap			cosϕ =				Bq
sin ϕ =	A2 p2 + B2q2 ,			cosϕ =				A2 p2 + B2q2 .
Тогда
	ψ =		Ap2	+ Bq2		K	O			(3.9)
	ψ =	A2 p2		+ B2q2		K				(3.9)
		A2 p2		+ B2q2
и					Ap2 (t)+ Bq2 (t)
				t	Ap2 (t)+ Bq2 (t)
	ψ =ψO + KO ∫0								dt. (3.10)
	ψ =ψO + KO ∫0				A2 p2 (t)+ B2q2 (t)				dt. (3.10)

Таким образом, углы Эйлера θ, ϕ и ψ могут быть найдены

из равенств (3.7), (3.8) и (3.10), если определены p(t), q(t), r(t).

Задача 3.1. Однородный эллипсоид с моментами инерции A, 32 A, 2A движется вокруг своего неподвижно

закрепленного центра масс. В начальный момент эллипсоиду сообщена угловая скорость Ω =ω 2i +ωk , где i , j, k -

единичные орты главных центральных осей инерции. Получить уравнения движения эллипсоида в квадратурах.

Решение. Динамические уравнения Эйлера в этом

случае

+ qr = 0,

3 dq

− 2 pr = 0,

(3.11)

4 dr

+qp = 0.

Умножив первое уравнение на p, третье – на r

и приравняв

затем левые части этих уравнений, получим

= 2r

→

p2 − p

= r2 −r

Так как pO = rO

2, то p = r

2 в любой момент времени.

Разделив первое уравнение (3.11) на второе, получим

уравнение с разделяющимися переменными

4 p dp = −3q dq.

Откуда

p2 =

(4 pO

−3q2 ),

−3q2 ).

и, кроме того,

r 2

(4 pO

Связь между p, q и r можно было получить и

непосредственно, используя интеграл энергии и закон сохранения кинетического момента:

<<< < Предыдущая 12 / 52 3 4 5 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
03.06.2015194.17 Кб14Теорфиз.Билеты.pdf
#
03.06.201545.59 Кб26Тест вводный физика - 10 кл 2013..pdf
#
03.06.201543.19 Кб22Тест вводный физика - 9 кл 2013..pdf
#
09.11.201960.42 Кб2ТЗ к Уставу Родной Партии.doc
#
03.06.201595.74 Кб6Тотальная мобилизация.doc
#
03.06.2015733.35 Кб50Трухан. Динамика твердого тела.pdf
#
27.03.2016796.04 Кб22ТРЯП 2015.pdf
#
03.06.2015653.46 Кб56ТФКП методичка.pdf
#
03.06.201510.77 Mб263ТФКП Половинкин.pdf
#
10.12.2018259.07 Кб0Т№12мет.указ. 2009.doc
#
10.12.2018183.3 Кб8Т№14 мет.указ. 2009.doc