
Sebery J.Cryptography.An introduction to computer security.1989
.pdf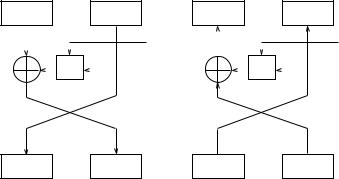
3.2 DES Family |
91 |
a ) Encryption |
|
|
|
|
|
b ) |
Decryption |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Li-1 |
|
|
|
|
R i-1 |
Li-1 |
|
|
R i-1 |
|||||
|
|
|
|
|
|
|
ki |
|
|
|
|
|
|
ki |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
f |
|
|
|
|
|
f |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||
Li |
R i |
Li |
R i |
Fig. 3.6. Feistel permutation
{Avalanche property { a single input bit change should force the complementation of approximately half of the output bits [169].
{Completeness property { each output bit should be a complex function of every input bit [266].
In general, to implement product ciphers, it is necessary to have two algorithms: one for encryption and the other for decryption. This can be expensive in terms of both hardware and software. Feistel [169] showed an elegant variant of S-P networks that could be implemented using a single algorithm for both encryption and decryption. A single round of this variant is shown in Figure 3.6. Note the following interesting properties of the round:
{It is always a permutation regardless of the form of the f function.
{As Li = Ri 1, the function f is evaluated on the same input for both encryption and decryption.
{ The design of a cipher E : |
K M ! C |
with |
M |
= |
C |
= n reduces to the |
|||||||||||||
|
|
n |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
design of the function f : K 2 |
! 2 |
|
where = f0; 1g. |
|
|
|
|
||||||||||||
De nition 1. A Feistel transformation |
is |
a permutation Fki |
: n |
n |
|||||||||||||||
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
(Li 1; R!i 1) = |
||||
that takes an input Li 1; Ri 1 2 2 |
and assigns the output Fki |
||||||||||||||||||
(Li; Ri) according to the following equations: |
|
|
|
|
|
|
|
|
|
|
|
||||||||
Li = Ri 1 and Ri = Li 1 f(ki; Ri 1); |
|
|
|
|
|
|
|
|
(3.3) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
n |
|
|
where the function f is any function of the form f : |
K 2 ! 2 and ki |
2 K |
|||||||||||||||||
is a cryptographic key (where stands for bit-by-bit XOR operation). |
|
||||||||||||||||||
92 3 PRIVATE-KEY CRYPTOSYSTEMS
A cryptographic system is called a Feistel-type cryptosystem if it applies ` rounds of a Feistel transformation (Feistel permutation) yielding an encryption function of the form:
Ek = Fk` Æ Fk` 1 Æ Æ Fk1 : |
(3.4) |
The decryption applies the inverse Feistel transformations in the reverse order. The cryptographic key is k = (k1; : : : ; k`).
An encryption algorithm should allow a user to select an encryption function from a large enough collection of all possible functions through the random selection of a cryptographic key. Note that for a plaintext/ciphertext block of n bits, the collection of all possible permutations contains 2n! elements and is called the symmetric group. If we assume that the size of the key block is also n bits, then the selection of permutations is restricted to 2n out of 2n! by random selection of the key. To generate a random permutation eÆciently, it is enough to iterate Feistel permutations many times. The single iteration is controlled by a shorter partial key which is usually generated from the cryptographic key. Therefore the iteration has to be seen as a collection of permutations, each of which is indexed by the partial key.
Coppersmith and Grossman [109] studied iterations of basic permutations and their suitability to encryption. They de ned the k-functions. Each k- function along with its connection topology produces a single iteration permutation which can be used as a generator of other permutations by composing them. Coppersmith and Grossman proved that these generators produce at least the alternating group using a nite number of their compositions. It means that using composition and with generators of relatively simple structure, it is possible to produce at least half of all the permutations. Even and Goldreich [165] proved that the Feistel permutations can also generate the alternating group. It turns out [408] that even if the function f (k; R) is restricted to one-to-one mappings, the Feistel permutations still generate the alternating
group. In other words, having (2n=2)! generators, it is possible to produce (2n)!
2
di erent permutations. Bovey and Williamson reported in [52] that an ordered pair of generators can produce either the alternating group AVn or the symmetric group SVn with the probability greater than 1 exp( log1=2 2n). So if we select the pair at random, there is a high probability that it generates at least
AVn .

3.2 DES Family |
93 |
3.2.2 Lucifer Algorithm |
|
The rst cryptosystem developed using Feistel transformations, was the Lucifer algorithm. It was designed at the IBM Watson Research Laboratory in the early 1970s by a team including Horst Feistel, William Notz, and J. Lynn Smith [169, 170, 487].
Lucifer cryptosystem |
|
|
|
|
|
|||
Message Space: M = 128. |
|
|
|
|
|
|||
Cryptogram Space: |
C = 128. |
|
|
|
||||
Key Space: K = 128, j K j= 2128, H(K)=128. A cryptographic key is k = |
||||||||
|
(k1; : : : ; k16). |
|
|
|
|
|
|
|
Encryption: Ek = Fk16 |
Æ Æ |
|
Fk1 . |
|
|
|||
Decryption: Dk = F |
1 |
Æ Æ |
F |
1 |
. |
|
||
1 |
k16 |
|
||||||
|
Unicity Distance: N |
H(K) |
40 letters (assuming D = 3:2). |
|
||||
|
D |
|
||||||
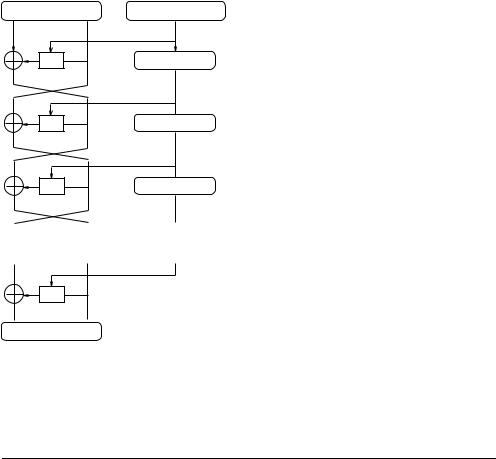
The Lucifer operates on 128-bit messages and encrypts them into 128-bit cryptograms under a 128-bit key. The general scheme of Lucifer is given in Figure 3.7. The core element is the function f (Figure 3.8). It translates 64-bit inputs into 64-bit outputs using a 64-bit partial key ki; i = 1; : : : ; 16. A 64-bit input Ri 1 to the function f goes to eight identical S-boxes. Each S-box is a simple substitution cipher with a single bit key (0 or 1). The eight bits needed to control S-boxes are extracted from the partial key ki. The outputs from S- boxes are XORed with the partial key ki. Finally, bits of the resulting sequence are permuted according to the xed wire-crossing topology of the block P.
The key schedule of Lucifer is very regular. Partial keys are selected from 64 lower bits of the key. After every extraction of the partial key, the contents of the 128-bit key register is rotated 56 bits to the left.
3.2.3 The DES Algorithm
The Data Encryption Standard (DES) [384] or Data Encryption Algorithm (DEA) was developed at IBM in the mid '70s and was the outgrowth of Lucifer. There is an interesting story behind the design and adoption of DES as a US encryption standard for nonmilitary applications. Readers are referred to Schneier's book [452] for details. It is no surprise to learn that the DES algorithm repeats the Lucifer general structure. The algorithm is summarized in
94 3 PRIVATE-KEY CRYPTOSYSTEMS
|
PLAINTEXT |
|
|
Key |
|
|
L |
64 |
R |
64 |
k1 |
k |
128 |
|
|
|
||||
|
|
f |
|
|
ROL 56-bits |
|
|
|
|
|
k2 |
|
|
|
|
f |
|
|
ROL 56-bits |
|
|
|
|
|
k3 |
|
|
|
|
f |
|
|
ROL 56-bits |
|
|
. |
|
. |
|
. |
|
|
. |
|
. |
|
. |
|
|
. |
|
. |
k16 |
. |
|
|
|
|
|
|
|
|
|
|
f |
|
|
|
|
|
CIPHERTEXT |
|
|
|
|
|
Fig. 3.7. Lucifer
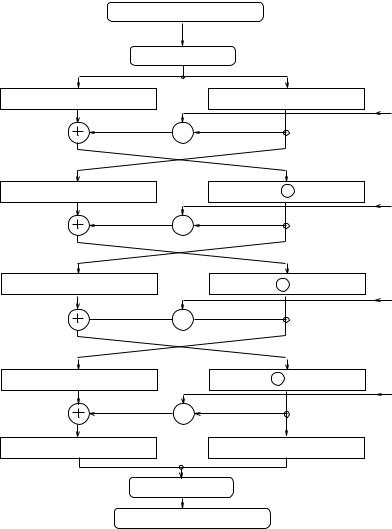
Figure 3.9. DES processes 64-bit blocks of data under a 56-bit key using 16 rounds (or iterations).
DES cryptosystem |
|
|
|
|
|
|
||
Message Space: M = 64. |
|
|
|
|
|
|||
Cryptogram Space: |
C = 64. |
|
|
|
|
|||
Key Space: K = 56, |
j K |
j= 256, H(K)=56. A cryptographic key is k = |
||||||
|
(k1; : : : ; k16). |
|
|
|
|
|
|
|
Encryption: Ek = Fk16 |
Æ Æ |
Fk1 . |
|
|
||||
Decryption: Dk = F |
1 |
Æ Æ |
F |
1 |
. |
|
||
1 |
k16 |
|
||||||
|
Unicity Distance: N |
H(K) |
17:5 letters (assuming D = 3:2). |
|
||||
|
D |
|
||||||
There was a disagreement over whether 56-bit key is suÆciently long. DiÆe and Hellman [153] had predicted the DES algorithm would be vulnerable to the exhaustive search attack by a special purpose machine. Indeed, Michael Wiener [529] at the Crypto '93 rump session gave technical details of a key search chip

|
|
|
3.2 DES Family |
95 |
|
|
ki |
|
|
L i-1 |
|
/ 8 |
R i-1 |
|
|
|
S |
|
|
|
|
S |
|
|
|
|
S |
|
|
|
P |
S |
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
S |
|
|
|
|
S |
|
|
R i |
|
S |
L i |
|
|
|
|
Fig. 3.8. Lucifer function f
which can test 5 107 keys per second. A search machine which uses 5760 chips will search the entire DES key space in 35 hours and cost $100,000.
The algorithm can be used for both encryption and decryption. An input x can be either a plaintext or a ciphertext block. The sequence x is rst transposed under an initial permutation (IP). The 64-bit output IP (x) is divided into halves L0 and R0. The pair (L0; R0) is subject to 16 Feistel transformations each of which uses the function f(ki; Li); i = 1; : : : ; 16. Finally, the pair (L16; R16) is transposed under the inverse permutation IP 1 to produce the output y. The permutations IP and IP 1 are given in Table 3.5. The IP and IP 1 tables (as well as the other permutation tables described later) should be read left-to- right, top-to-bottom (e.g. IP transposes a binary string x = (x1x2 : : : x64) into (x58x50 : : : x7)). All tables are xed.
Note that after the last iteration, the left and right halves are not exchanged; instead the concatenated block (R16L16) is input to the nal permutation IP 1. This is necessary to ensure that the algorithm can be used both to encipher and decipher.
The Function f and S-boxes. Figure 3.10 shows the components of the function f(ki; Ri 1). First Ri 1 is expanded to a 48-bit string E(Ri 1) using the bit-selection function E shown in Table 3.6. This table is used in the same way as the permutation tables, except that some bits of Ri 1 are selected more
96 3 PRIVATE-KEY CRYPTOSYSTEMS
PLAINTEXT
IP
L 0 |
R 0 |
f
L 1 = R 0 |
R 1 = L 0 + f (R 0 , k1 ) |
f
L 2 = R1 |
R |
2 |
= L |
1 |
+ |
f ( R , k |
2 |
) |
|
|
|
|
1 |
|
|||
|
f |
|
|
|
|
|
|
|
L 15 = R14 |
R 15 = L14 |
+ |
f ( R 14 , k 15 ) |
|||||
|
f |
|
|
|
|
|
|
|
R 16 |
|
|
|
|
L 16 |
|
|
|
IP -1
CIPHERTEXT
Fig. 3.9. Data Encryption Standard
k1
k 2
k16
than once; thus, given Ri 1 = r1r2 : : : r32, E(Ri 1) = r32r1r2 : : : r32r1. Next, the XOR of E(Ri 1) and ki is calculated and the result is broken into eight 6-bit blocks B1; : : : ; B8, where
E(Ri 1) ki = B1B2 : : : B8:
Each 6-bit block Bj is then used as the input to a selection (substitution) function (S-box) Sj, which returns a 4-bit block Sj(Bj). These blocks are concate-

3.2 DES Family |
97 |
58 50 42 34 26 18 10 2
60 52 44 36 28 20 12 4
62 54 46 38 30 22 14 6
64 56 48 40 32 24 16 8
57 49 41 33 25 17 9 1
59 51 43 35 27 19 11 3
61 53 45 37 29 21 13 5
63 55 47 39 31 23 15 7
(a)
40 8 48 16 56 24 64 32
39 7 47 15 55 23 63 31
38 6 46 14 54 22 62 30
37 5 45 13 53 21 61 29
36 4 44 12 52 20 60 28
35 3 43 11 51 19 59 27
34 2 42 10 50 18 58 26
33 1 41 9 49 17 57 25
(b)
Table 3.5. (a) Initial permutation IP and (b) Final permutation IP 1
R i-1 (32 bits)
E
48 bits |
k i (48 bits) |
S1 |
S 2 |
S 3 |
S 4 |
S5 |
S 6 |
S 7 |
S8 |
P
32 bits
Fig. 3.10. DES function f(ki; Ri 1)
nated together, and the resulting 32-bit block is transposed by the permutation P shown in Table 3.7. Thus, the block returned by f(ki; Ri 1) is
P (S1(B1) : : : S8(B8)):
Each S-box Sj maps a 6-bit sequence Bj = b1b2b3b4b5b6 into a 4-bit sequence as de ned in Table 3.8. This is done as follows: The integer corresponding to b1b6 selects a row in the table, while the integer corresponding to b2b3b4b5 selects a column. The value of Sj(Bj) is then the 4-bit representation of the integer in that row and column. For example, if B1 = 011100, then S1 returns the value in row 0, column 14; this is 0, which is represented as 0000. If B7 = 100101,

98 3 PRIVATE-KEY CRYPTOSYSTEMS
32 |
1 |
2 |
3 |
4 |
5 |
4 |
5 |
6 |
7 |
8 |
9 |
8 |
9 10 |
11 |
12 13 |
||
12 |
13 14 |
15 |
16 17 |
||
16 |
17 18 |
19 |
20 21 |
||
20 |
21 22 |
23 |
24 25 |
||
24 |
25 26 |
27 |
28 29 |
||
28 |
29 30 |
31 |
32 |
1 |
|
|
|
|
|
|
|
Table 3.6. Bit-selection function E
16 7 20 21
29 12 28 17
1 15 23 26
5 18 31 10
2 8 24 14
32 27 3 9
19 13 30 6
22 11 4 25
Table 3.7. Permutation P
then S7 returns the value in row 3, column 2; this is 13, which is represented as 1101.
Although the DES algorithm was made public, the collection of tests used to select S-boxes and the P-box was not revealed until 1994 [108]. The collection of tests is equivalently referred in the literature as the design criteria/properties. A summary of the design properties used during the design of S-boxes and the P-box can be found in [67] and [380]. Some S-box design properties are:
{Each row function in an S-box is a permutation (S-boxes produce sequences with balanced number of zeroes and ones).
{No S-box is linear or aÆne function of the input (S-boxes are nonlinear),
{A single-bit change on the input of an S-box changes at least two output bits (S-boxes provide \avalanche" e ect).
{For each S-box S, S(x) and S(x 001100) must di er in at least two bits.
{S(x) 6= S(x 11ef 00) for any choice of bits e and f.
{The S-boxes minimize the di erence between the number of ones and zeroes
in any S-box output when any single bit is constant.
3.2 DES Family |
99 |
S-box design criteria can be de ned using the information theory concept of mutual information. This approach was applied by Forre in [188] and Dawson and Tavares in [128]. They argued that the mutual information between inputs and outputs of S-boxes should be as small as possible. The study of the DES S-boxes gave rise to a new eld called the S-box theory.
Davies [124] and Davio, Desmedt, Goubert, Hoornaert and Quisquater [125] analyzed the concatenation of the P-box and bit-selection function E. Assume that the input to an S-box is abcdef. The following observations can be made [67]:
{Each S-box input bit comes from the output of a di erent S-box.
{No input bit to a given S-box comes from the output of the same S-box.
{An output from Si 1 goes to one of the ef input bits of Si and further via E an output from Si 2 goes to one of the ab input bits.
{An output of Si+1 goes to one of the cd inputs bits of Si.
{For each S-box output, two bits go to ab or ef input bits, the other two go to cd input bits.
The above properties allow a quick di usion of partial cryptograms between two consecutive rounds.
DES Key Scheduling. Each iteration uses a di erent 48-bit key ki derived from the initial key k. Figure 3.11 illustrates how this is done. The initial key is input as a 64-bit block, with 8 parity bits in positions 8, 16, : : :, 64. The permutation PC1 (permuted choice 1) discards the parity bits and transposes the remaining 56 bits as shown in Table 3.9. The result, PC1(k), is then split into halves C0 and D0 used to derive each partial key ki. Subsequent values of (Ci; Di) are calculated as follows:
Ci = LSs(Ci 1); Di = LSs(Di 1);
where LSs is a left circular shift by the number of positions shown in Table 3.10. Key ki is then given by,
ki = P C2(CiDi)
where PC2 is the permutation shown in Table 3.11.
The key schedule works well for most keys. However, if the key is k = 01010101 01010101x, then all partial keys are ki = 0000000 0000000x where the

100 3 PRIVATE-KEY CRYPTOSYSTEMS
Key (64 bits)
PC1
C 0 (28 |
bits) |
D0 |
(28 |
bits) |
|
|
|
LS |
|
|
LS |
|
|
C1 |
(28 |
bits) |
D1 |
(28 |
bits) |
|
|
|
|
|
|
k |
1 |
|
|
|
|
|
PC2 |
|
|
LS |
|
|
LS |
|
|
C 2 |
(28 |
bits) |
D2 |
(28 |
bits) |
|
|
|
|
|
|
k |
2 |
|
|
|
|
|
PC2 |
|
|
. |
|
|
. |
|
|
|
. |
|
|
. |
|
|
|
. |
|
|
. |
|
|
LS
C16 (28 bits)
LS
D16 (28 bits)
k |
16 |
PC2 |
|
Fig. 3.11. DES key schedule
subscript x denotes a hexadecimal number. Note the key k has 8 parity bits which are stripped o later in the key scheduling. In general, all keys whose partial keys are the same must be avoided. These keys are termed as weak keys. DES has 16 weak keys. There is also a class of semiweak keys. A key is called semiweak if the key scheduling scheme produces two di erent partial keys only (instead of 16).
3.2.4 DES Modes of Operation
Encryption and decryption are usually done for larger than 64-bit blocks of data. The method of processing a large number of 64-bit data blocks is called the mode of operation. There are several modes of operation, including the following four most common ones:
