
Joye M.Cryptographic hardware and embedded systems.2005
.pdf
226 L.D. Olson
Thus
Putting all this together, we can now state the group law on the weighted quartic  formally.
formally.
Proposition 1. |
Let |
be the elliptic |
curve given by the weighted quartic |
|
curve |
|
|
in |
Let |
and |
be |
points in |
|
such that |
|
|
Let |
|
Then |
We note that the proposition accomplishes two objectives:
a.) it gives a uniform description of the group law on the weighted quartic 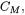 i.e. the addition formula is independent of whether
i.e. the addition formula is independent of whether  or not.
or not.
b.) the group law is given entirely in terms of the coefficients of the equation for 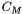 and the coordinates of the
and the coordinates of the 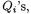 making no explicit reference to the curve E and the point M which we had as our starting point. While this is not used in the sequel, it may prove to be of some independent interest.
making no explicit reference to the curve E and the point M which we had as our starting point. While this is not used in the sequel, it may prove to be of some independent interest.
To make the group law more accessible and to evaluate its usefulness, we provide an algorithm for its computation in the next section.
4An Algorithm for the Group Law
We will now give an explicit algorithm for the computation of  in terms of weighted projective coordinates and count the number of multiplications involved. We define quantities
in terms of weighted projective coordinates and count the number of multiplications involved. We define quantities 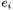 and
and  for
for  in terms of the
in terms of the 
 and
and 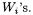 The operations used to obtain the
The operations used to obtain the 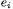 will consist of addition/subtraction and multiplication by integer constants
will consist of addition/subtraction and multiplication by integer constants 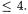 The operation involved in the computation of the
The operation involved in the computation of the  will be a single multiplication. This will enable us to keep track of the number of multiplications involved in a convenient fashion. Define
will be a single multiplication. This will enable us to keep track of the number of multiplications involved in a convenient fashion. Define
TEAM LinG

Side-Channel Attacks in ECC 227
Some computation yields the following useful formulas
From Proposition 1 and these formulas, we have that
From this we see that the algorithm sketched above requires 31 multiplications including all necessary multiplications by the  In contrast, the algorithm given in Brier and Joye ([6]) for elliptic curves in Weierstrass form requires 17 multiplications plus 1 multiplication with a constant from the equation.
In contrast, the algorithm given in Brier and Joye ([6]) for elliptic curves in Weierstrass form requires 17 multiplications plus 1 multiplication with a constant from the equation.
TEAM LinG

228 L.D. Olson
5Applications to Side-Channel Attacks
In the previous sections, we showed how to attach to any elliptic curve E and any  point
point 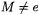 on E an isomorphic elliptic curve
on E an isomorphic elliptic curve 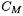 which is given as a weighted quartic projective curve.
which is given as a weighted quartic projective curve.
The first advantage of this representation is that the addition P + Q of two points may be expressed by formulas independent of whether or not P and Q are different. This uniformity defends against SPA.
Standard techniques of defending against DPA involve either using projective coordinates or changing the representation of the elliptic curve. The method outlined offers both of these features. The addition may be carried out with projective coordinates as indicated above.
Another advantage is that this representation is available for all elliptic curves. Thus, it may be applied to all curves included in present and future standards.
Each elliptic curve admits of a large number of such representations, which can be changed at virtually no cost.
6Examples
A crucial point with this approach is that we may choose any point 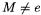 on E to obtain a new parametrization. Some applications may not mandate this and it is of some interest to examine certain special examples. We begin by looking at the work of Billet and Joye ([3]) which sparked our interest to begin with.
on E to obtain a new parametrization. Some applications may not mandate this and it is of some interest to examine certain special examples. We begin by looking at the work of Billet and Joye ([3]) which sparked our interest to begin with.
Example 1. (Billett-Joye). An important example of our construction is to be found in the Jacobi model of Billett and Joye ([3]) and its application to sidechannel attacks. They begin with an elliptic curve E defined by the affine Weierstrass equation
and a 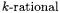 point
point  of order 2. Applying the procedure outlined above, we obtain the curve
of order 2. Applying the procedure outlined above, we obtain the curve
where 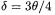 and
and  A simple change of variables then gives the equation
A simple change of variables then gives the equation
used by Billet and Joye.
Example 2. A situation which leads to a particularly simple quartic is the use of a point 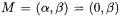 where the X -coordinate of M is 0. This yields the quartic
where the X -coordinate of M is 0. This yields the quartic
TEAM LinG
Side-Channel Attacks in ECC |
229 |
References
1.Liardet, P.-V., Smart, N.B.: Preventing SPA/DPA in ECC Systems Using the Jacobi Form. In: Ç.K. Koç, D. Naccache, and C Paar, editors, Cryptographic Hardware and Embedded Systems – CHES 2001, Volume 2162 of Lecture Notes in Computer Science, pages 391-401. Springer-Verlag, 2001.
2.Joye, M., Quisquater, J.-J.: Hessian Elliptic Curves and Side-Channel Attacks. In: Ç.K. Koç, D. Naccache, and C Paar, editors, Cryptographic Hardware and Embedded Systems – CHES 2001, Volume 2162 of Lecture Notes in Computer Science, pages 402-410. Springer-Verlag, 2001.
3.Billet, O., Joye, M.: The Jacobi Model of an Elliptic Curve and Side-Channel Analysis. In: Fossorier, M.,Høholdt, T.,Poli, A., editors, Applied Algebra, Algebraic Algorithms and Error-Correcting Codes, Volume 2643 of Lecture Notes in Computer Science, pages 34-42, Springer-Verlag, 2003.
4.Reid, M. Graded rings and varieties in weighted projective space. Manuscript, M. Reid’s Web page (www.maths.warwick.ac.uk/˜miles/surf/more/grad.pdf), Jan. 2002.
5.Fricke, R. Die elliptische Funktionen und ihre Anwendungen, B.G. Teubner, 1922.
6.Brier, É., Joye, M.: Weierstraß Elliptic Curves and Side-Channel Attacks. In: Naccache, D and Paillier, P., editors, Public Key Cryptography 2002, Volume 2274 of Lecture Notes in Computer Science, pages 335-345. Springer-Verlag, 2002.
TEAM LinG
Switching Blindings with a View Towards IDEA
Olaf Neiße and Jürgen Pulkus
Giesecke & Devrient, Department of Cryptology, Prinzregentenstr. 159,
81677 Munich, Germany
Abstract. Cryptographic algorithms implemented on smart-cards must be protected against side-channel attacks. Some encryption schemes and hash functions like IDEA, RC6, MD5, SHA-1 alternate various arithmetic and boolean operations, each of them requiring a different kind of blinding. Hence the maskings have to be changed frequently. How to switch reasonably between standard arithmetic masking and boolean masking was shown in [2], [3], [5] and [9].
In this paper we propose more space-efficient table-based conversion methods. Furthermore, we deal with some non-standard arithmetic operations, namely arithmetic modulo  for some
for some  and a special multiplication used by IDEA.
and a special multiplication used by IDEA.
Keywords: DPA, IDEA, MD5, Masking Techniques, RC6, SHA-1.
1Introduction
Running cryptographic algorithms on systems vulnerable to side-channel attacks (e.g., on smart-cards), implementation issues become crucial and non-trivial. By side-channel information we mean all information a physical system leaks into the environment, like computation time, power consumption, electromagnetic emissions. In the literature a variety of attacks is known that exploit side-channels to gain sensitive information like secret keys. Attacks based on statistical examinations, such as Differential Power Analysis (DPA) [6], Differential Electromagnetic Analysis (DEMA) [1],[11] and higher-order DPA, force special protection and therefore special and careful implementations. One way to counteract this problem is to randomly split sensitive data into at least two shares such that computations can be carried out by manipulating only the shares, never reconstructing the original data. In case of two shares we call the two parts masked data and mask.
Some encryption schemes like IDEA [7], TWOFISH [4] or RC6 [12] and some hash functions like MD5, SHA-1 (see [8]) or SHA-2 [10] use the concept of “incompatible mixed group operations” to achieve the desired confusion and diffusion. The most frequent group structures employed by the designers are the boolean operation 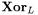 (addition on
(addition on  and the standard arithmetic operation
and the standard arithmetic operation 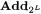 (addition on
(addition on 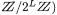 for some integer L, mainly L = 8,16,32 or 64. But non-standard arithmetic operations like multiplication
for some integer L, mainly L = 8,16,32 or 64. But non-standard arithmetic operations like multiplication  on
on
are used as well. The masking has to be adapted to these group
M. Joye and J.-J. Quisquater (Eds.): CHES 2004, LNCS 3156, pp. 230–239, 2004. |
|
© International Association for Cryptologic Research 2004 |
TEAM LinG |

Switching Blindings with a View Towards IDEA |
231 |
structures. If such group operations are mixed in a scheme, one has to convert the masking. Methods for switching masks between boolean and standard arithmetic are presented in [2], [3], [5] and [9]. Unlike the conversion from 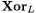 to
to 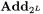 (using the very efficient method proposed by Goubin [5]) the contrary direction still waits for a timeand space-efficient method.
(using the very efficient method proposed by Goubin [5]) the contrary direction still waits for a timeand space-efficient method.
In Section 3 we present Algorithm 3.2 which transforms 
into  using a compressed table. In comparison to the method proposed by Coron and Tchulkine in [3] our algorithm requires only half the memory for tables. In Section 4 we explain how to use our table to enable switching from
using a compressed table. In comparison to the method proposed by Coron and Tchulkine in [3] our algorithm requires only half the memory for tables. In Section 4 we explain how to use our table to enable switching from  to
to  and conversely. As an application we show in Sect. 5 how to implement the block cipher IDEA [7] efficiently and securely.
and conversely. As an application we show in Sect. 5 how to implement the block cipher IDEA [7] efficiently and securely.
2Notation
Since several kinds of operations with varying length or modulus have to be mixed in our investigation, we use the following notation: For  let
let
set of bit sequences of length 
also viewed as set of integral numbers 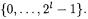 infix-notation for bitwise exclusive or
infix-notation for bitwise exclusive or
infix-notation for addition modulo  prefix-notation for subtraction modulo
prefix-notation for subtraction modulo 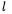 infix-notation for subtraction modulo
infix-notation for subtraction modulo 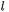 infix-notation for multiplication modulo
infix-notation for multiplication modulo 
–0 |
bit sequence ( 0 , 0 , . . . , 0) |
–1 |
bit sequence (1,1,..., 1) |
|
1-complement of |
|
concatenation of the bit sequences |
|
logical shift right by 1: |
|
comparison function |
3 From |
to |
|
|
|
Throughout the paper we start with some sensitive |
data |
(with |
||
mainly L = 8,16,32) given by a mask |
and the masked data using one type |
|||
of masking. Our goal is always to switch blinding so that |
is then represented |
|||
by a new mask |
and masked data with respect to another masking. For this |
|||
we use randomized tables of size |
where |
is a small divisor of L, e.g. |
||
|
or (16,4). An additional random bit |
will be needed to |
||
make the calculation DPA-resistant. For variables we signal a certain dependency
TEAM LinG

232 |
O. Neiße and J. Pulkus |
|
|
on by a tilde. Setting |
and |
the elements of V(L) are viewed |
|
as the |
numbers |
from 0 to M – 1. |
|
Now suppose that  is represented using a standard arithmetic masking. We describe algorithms that perform the conversion into a boolean masking of
is represented using a standard arithmetic masking. We describe algorithms that perform the conversion into a boolean masking of 
The easiest DPA-resistant algorithm precomputes, depending on 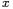 and
and  one big table
one big table  which contains for every value
which contains for every value  the corresponding value
the corresponding value  The conversion is done by a simple table-lookup. This is fast during the computation; however, for L large this algorithm is not practical because generating the table S needs too much time and space. We overcome this problem by working with such a table S only virtually – i.e. the entries of S are calculated using smaller tables T and C.
The conversion is done by a simple table-lookup. This is fast during the computation; however, for L large this algorithm is not practical because generating the table S needs too much time and space. We overcome this problem by working with such a table S only virtually – i.e. the entries of S are calculated using smaller tables T and C.
The basic idea is similar to the approach presented by Coron and Tchulkine
in [3, 3.2]: one precomputes a small randomized table |
which |
|||||
turns an |
|
digit for some input-falsifier |
into an |
digit for an |
||
output-falsifier |
With the help of this table, the result is calculated iteratively |
|||||
digit by |
digit from the lowest |
to the highest. More precisely, the |
digits |
of |
||
|
|
are calculated in the additively masked form |
and |
then |
||
plugged into the table T to switch securely into the |
|
with |
||||
falsifier |
So one needs to find the masked digits |
using |
and |
Let |
||
|
|
and |
Then |
|
|
|
for some carry bits In order to correct the digit of to one needs to determine the carry bit  which equals 1 in
which equals 1 in 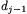 out of
out of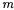 cases and therefore
cases and therefore
is susceptible to DPA. Hence a carry bit table providing the information, if the addition  yields a carry mod
yields a carry mod  or not, has to be randomized.
or not, has to be randomized.
Coron and Tchulkine propose in [3, Algorithm 4] to work with a random mask  and the table
and the table 
Our solution works with the much smaller bit-table 
 We do not randomize the carry bit table directly, instead we blind the carry bit information during the conversion itself by a single random bit
We do not randomize the carry bit table directly, instead we blind the carry bit information during the conversion itself by a single random bit  (described below).
(described below).
Furthermore, the operations  and
and  coincide on the least significant bit (LSB). Hence we can spare the LSB of each entry
coincide on the least significant bit (LSB). Hence we can spare the LSB of each entry  and replace it by the carry bit
and replace it by the carry bit 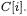 This enables us to store
This enables us to store  and
and  in one table, whereas Coron and Tchulkine needed twice the space.
in one table, whereas Coron and Tchulkine needed twice the space.
This explains our precomputation:
TEAM LinG

Switching Blindings with a View Towards IDEA |
233 |
Our switching algorithm 3.2 uses the following fact: the addition |
con- |
|||||
tributes in |
out of |
cases |
a carry bit = 1, |
balancing out the |
||
cases when the carry bit is 1 for |
|
Therefore we work with |
or its one- |
|||
complements, depending on a randomly chosen bit |
|
|
||||
For a variable let |
denote |
if |
and |
if |
so |
|
The computations are based on the following observation: For |
let |
|||||
Then |
|
|
|
|
|
|
Especially, |
Solving for and adding |
on both sides gives |
||||
|
which is in case |
just what we wanted to |
||||
calculate above. In case |
we do the same calculation, but the role of is |
|||||
taken by its complement  with two consequences: each additively masked digit plugged into the table yields the complement of the result of the case
with two consequences: each additively masked digit plugged into the table yields the complement of the result of the case 
This can be corrected easily. And, instead of reading the carry |
of the addition |
from the carry table, we read the carry of the addition |
|
Although the steps look rather complicated, they mostly describe elementary operations on a processor.1 Steps (3) and (4) are precalculations supporting the mask changes in Steps (8), (9) and (11) from  and
and 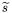 to
to  and
and  respectively. They could also be part of the loop. All intermediate variables and all carry bits
respectively. They could also be part of the loop. All intermediate variables and all carry bits
1 Steps (8) and (9) could even be done at the same time by a subtraction with carry, but then the change of the carry bit would not be independent of the data 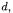 which might cause troubles on certain platforms.
which might cause troubles on certain platforms.
TEAM LinG

234 O. Neiße and J. Pulkus
in (8)-(11), as |
well as all changes of these values are independent of whence |
this algorithm |
turns out to be DPA-resistant. Indeed, all values depending on |
for 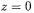 are calculated in the case
are calculated in the case 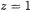 using the complement of
using the complement of 
The algorithm can be varied in many ways: instead of starting with a mask
and a masked value |
one can also work with two shares and |
||
For this, one just has to replace some subtractions by additions. Or, |
|||
one can calculate in the loop instead of |
the value |
For this, one has |
|
to modify the tables by using additions instead of subtractions.
For practical implementations on a chip card one might use either one table of size 256 bytes or sixteen tables of size 16 nibbles each. In the latter case one can generate all tables with pairwise different input and output randomizations (in random order) and then use different tables in each round of the loop. As for all possible input randomizations there is a table available in RAM, one can choose in Step (3) instead of  an arbitrary value. For example one can make
an arbitrary value. For example one can make  to zero, such that the subtraction in Step (9) in the loop can be skipped.
to zero, such that the subtraction in Step (9) in the loop can be skipped.
4From 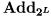 to
to 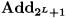 and Back
and Back
In this section we deal with the question how to switch between standard arithmetic masking modulo  and additive maskings modulo
and additive maskings modulo 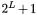 without leaking any information about the data. Our solution is based on the following fact:
without leaking any information about the data. Our solution is based on the following fact:
Proposition 4.1. Let |
|
|
|
i) |
For |
let |
and |
|
Then |
|
|
ii) |
For |
let |
and |
|
Then |
|
|
Proof. We first examine the case 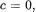 that is
that is  and therefore
and therefore Both conclusions are obvious except if
Both conclusions are obvious except if  where in fact
where in fact 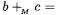
 The case
The case  follows immediately from
follows immediately from 
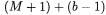 for i) and
for i) and  for ii).
for ii).
So we just have to add respectively subtract the carry bit  As before, this bit is correlated to the sensitive data
As before, this bit is correlated to the sensitive data 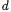 and therefore has to be randomized.
and therefore has to be randomized.
Starting from an additive mask modulo  the carry bit can be determined employing the same ideas we have seen in Algorithm 3.2: for masks
the carry bit can be determined employing the same ideas we have seen in Algorithm 3.2: for masks  of the special form
of the special form  the carry bit
the carry bit 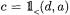 equals the bit
equals the bit  in
in 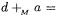
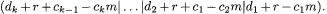 In Algorithm 3.2, Step
In Algorithm 3.2, Step
(10) for  yields
yields 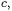 masked with the chosen bit
masked with the chosen bit  Hence we adapt Algorithm
Hence we adapt Algorithm
3.2to our new problem such that  is computed without leaking information.
is computed without leaking information.
Starting from an additive mask modulo 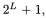 additional to the ideas of Sect. 3 more ideas are needed, since the special value
additional to the ideas of Sect. 3 more ideas are needed, since the special value  has to be treated differently. However, since
has to be treated differently. However, since  is not a divisor of
is not a divisor of  not all intermediate values are totally independent of
not all intermediate values are totally independent of  Few values show weak dependency which should not leak side channel information in practice.
Few values show weak dependency which should not leak side channel information in practice.
TEAM LinG

Switching Blindings with a View Towards IDEA |
235 |
Both conversion algorithms employ the unmasked carry bit table C:
Before going into details of the algorithms, we give an analogue of the formula 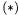 for calculations modulo
for calculations modulo  We use the notation
We use the notation
where, as usual, |
|
with |
and |
for |
For |
and |
this is the usual one-complement. |
|
|
Let |
Then an easy calculation shows: |
|
|
|
This formula is helpful in verifying the correctness of our algorithms. Another fact one should keep in mind is: instead of adding two elements of V(L) modulo M + 1 one can add them modulo M, if the occuring carry is later subtracted modulo M + 1. For subtraction the carry has accordingly to be added modulo M + 1.
Subsequently we propose our conversion Algorithm 4.3 for the transformation
As mentioned above, we modify Algorithm 3.2 for our purpose. Clearly Steps (2), (4), (11), (13) and the first half of (10) in 3.2 can be skipped. The new steps will be explained below.
TEAM LinG
