
диафрагмированные волноводные фильтры / 8108c36b-00e6-444d-b2d1-ccf07883ddc6
.pdf
2018 IEEE MTT-S International Conference on Numerical Electromagnetic and Multiphysics Modeling and Optimization (NEMO)
Complex Eigenmodes for Modelling of Dielectric Dual-Mode Resonators
Michael Hoft¨ and Daniel Miek
Kiel University, Institute for Electrical Engineering and Information Technology, Chair of Microwave Engineering, Kaiserstr. 2, D-24143 Kiel, Germany fmh,damig@tf.uni-kiel.de
Abstract—In this paper, concepts for dielectric dual-mode resonators will be reviewed. Based on this review a new concept for modelling of a resonator is presented, which is based on complex eigenmodes. Their existence is revealed by a simple eigenmode approach using branch-vector representation and rotational symmetry of the physical structure. The resulting modes can be interpreted as circular polarized modes, which gives more insight into the structure and might lead to novel design concepts for bandpass filter design.
I. INTRODUCTION
y |
y |
E2 |
E3 |
y |
|
E2 |
|
|
y |
||||
|
|
|
E4 |
|
|
E3 |
|
|
E1 |
|
|
E1 |
|
|
|
|
|
|
||
|
z |
|
x |
|
z |
x |
(a) |
(b) |
Fig. 1. (a) Conventional dielectric dual-mode resonator with X-shape (b) Dielectric dual-mode resonator with Y-shape.
Dielectric dual-mode resonators are attractive for realization of compact bandpass filters designs. The dielectric resonators considered in this paper are based on TM-mode operation in dielectric rods, as first reported in [1]. The ceramic is located with contact to bottom and top in the center of the housing, focusing the electric field along the rod, while the magnetic field is rotating transversal around it. Dual-mode operation is achieved by arrangement of two perpendicular rods as shown in Fig. 1(a). Usually, degeneration of the modes is explained as follows: Two modes with identical performance exist, one with horizontal polarization and one with vertical polarization. Degeneration is then explained by mirror symmetry along the diagonal axis. Perturbation along the diagonal axis is then applied to couple the modes. As well known, this series coupled resonator explanation for bandpass filter design can also be explained by parallel excitation of an alternative set of diagonal polarized modes [2], [3], [4]. Besides the mirror symmetry also rotational symmetry of the physical structure can be taken into account to explain degeneration of modes. By proper arrangement of dielectric rods in branch configuration, new fundamental eigenmode resonances can be shown to be present [5]. In the simplest case, dual-mode operation is achieved by an Y-shape arrangement [6], as depicted in Fig. 1(b). Results for a related dual-mode two pole bandpass filter have been discussed in [7]. In Section II the concepts for dielectric dual-mode resonators and in Section III the eigenmode approach are reviewed. Based on these results, Section IV explains an alternative solution leading to complex eigenmodes. Section V concludes this study.
II. FUNDAMENTAL OPERATION
The perpendicular arrangement of two dielectric rods to achieve conventional dual-mode operation as shown in
978-1-5090-4837-3/17/$31.00 c 2017 IEEE
Fig. 1(a) can also be interpreted as being constructed of n = 4 dielectric branches, which are connected from the center node to the cavity walls [5]. The branches are spaced apart with 90 rotation angle, whereas the Y-shape dual-mode resonator as shown in Fig. 1(b) consists of only n = 3 dielectric branches, which are spaced apart with 120 rotation angle.
A. Field representatives and orthogonality
Since the ceramic branches focus and guide the electric field, a simple approximation model for the fundamental modes is introduced. It is based on a single scalar value Ei for an effective electric field strength representing the vector field in each branch i with its effective volume Vi. The effective electric fields have already been indicated in Fig. 1. The approximation is based on the assumption, that there are no serious changes along the branch (e.g. no =2 resonances) and basically negligible perpendicular components of the electric fields. Consequently, related higher order modes are neglected.
With these definitions the condition for orthogonality [8] of two eigenmodes j and k can be expressed as
Zn
X
~ ~ ~ ~
< Ej; Ek >= Ej EkdV = Ei;jEi;k Vi = 0 (1)
Vi=1
for all j 6=k, where the volume V covers the whole cavity and the scalar values Ei for the n branches are combined in
~ |
~ |
for the eigenmode j=k, respectively). |
a vector E |
(Ej=k |
To further describe the geometrical setup effective areasAi are introduced, as sketched in Fig. 2 for the center node
of the Y-shape resonator. To fulfil the continuity equation |
|
IS(J~ + j! E~ ) dA~ = 0; |
(2) |
one obtains: |
|
E1 A1 + E2 A2 + E3 A3 = 0: |
(3) |
978-1-5386-5204-6/18/$31.00 ©2018 IEEE

2018 IEEE MTT-S International Conference on Numerical Electromagnetic and Multiphysics Modeling and Optimization (NEMO)
V3




 E3
E3
|
A3 |
|
S |
V2 |
A2 |
|
DA |
|
|
||
|
|
A1 |
V1 |
|
E2 |
|
|
|
|
|
E1 |
Fig. 2. Details of branch model: Center node of the Y-shape resonator.
(A) |
(B) |
Fig. 4. Electric fields of the fundamental eigenmodes (a) mode with H-plane symmetry, (b) mode with E-plane symmetry [5].
(A)
(A) |
(B) |
(C) |
(B) |
|
Fig. 3. Electric fields of the fundamental eigenmodes of the X-shape resonator: (a) Vertical polarization, (b) horizontal polarization, (c) spurious mode.
Fig. 5. Superposition of rotated versions of H-plane mode: (a) Constructive to reobtain H-plane, (b) destructive to obtain E-plane mode [5].
Note that due to symmetry all effective volumes Vi and areasAi are identical.
B. Resulting eigenmode solutions: X-shape resonator
The electric field distribution of the degenerated eigenmodes of the X-shape resonator is visualized in Figs. 3(a) and (b). In Fig. 3(c) a spurious mode is shown, which also fulfils the orthogonality and continuity equation as discussed in the last section. Note that, if the geometry of the resonator is properly chosen, this mode can be set to have the same resonance frequency as the degenerated modes to obtain triple-mode operation [9]. The normalized branch-vector representation of the three eigenmodes with designation from Fig. 1(a) is given
by |
2 |
03; E~ |
2 = |
1 |
2 |
13 |
and E~3 = 1 |
2 13: (4) |
||||
E~1 = 1 |
||||||||||||
|
|
|
1 |
|
|
|
6 |
0 |
|
|
6 |
1 |
p2 |
6 07 |
|
p2 |
17 |
2 |
17 |
||||||
|
|
6 |
7 |
|
|
|
6 |
7 |
|
|
6 |
7 |
|
|
4 |
1 |
|
|
|
4 |
0 |
|
|
4 |
1 |
|
|
5 |
|
|
|
5 |
|
|
5 |
|||
C. Resulting eigenmode solutions: Y-shape resonator
The electric field distribution of the degenerated eigenmodes of the Y-shape resonator are shown in Fig. 4. Unlike the X- shape resonator there is no spurious mode excited by focusing and guiding the electric field along the branches. Hence, the spurious mode performance is improved as discussed in [7].
The orthogonal modes exhibit zy-plane symmetry. For the H-plane/E-plane symmetry of Fig. 4(a)/(b), the magnetic/electric field is perpendicular to this plane, respectively. For the H-plane mode, the field of one branch splits up into two parts flowing into the other branches, while for the E-plane mode, fields are only dominant in two branches
[5]. The normalized branch-vector representation of the two eigenmodes with designation from Fig. 1(b) is given by
E~1 = p |
2 13 |
and E~2 = p |
2 |
13: |
(5) |
|||
1 |
|
2 |
1 |
|
0 |
|
||
4 |
15 |
4 15 |
|
|||||
|
6 |
|
2 |
|
||||
It is not obvious from the shown field distributions, that both eigenmodes are having the same resonance frequency. Nevertheless, the degeneration of the eigenmodes can be proven by considering the 120 rotational symmetry of the resonator [5], [7]: In Fig. 5(a) the two possible rotated versions of the H-plane mode are shown. Furthermore, one can see that if they are constructively superposed the original H-plane mode is reobtained. On the other hand, the E-plane mode is obtained, if they are destructively superposed as shown in Fig. 5(b). As a result, E-plane and H-plane modes are not independent from each other, i.e. showing degeneration causing dual-mode operation.
D. Exemplary Y-shape filter design
A related dielectric dual-mode bandpass filter has been designed [7]. Instead of contacting the branches to the sidewalls of the housing, the ceramic resonator was manufactured to contact all three branches to the bottom as depicted in Fig. 6. The filter was laid out based on the H-plane/E-plane symmetry as shown in Fig. 4 and parallel excitation of the modes. Due to their different field distributions, the modes cannot be excited with equal strength. As consequence, a transmission zero occurs in the design – a second one due to source-load-coupling. The measurement results are shown in Fig. 7 and compared with the result of the extracted transversal coupling matrix.

2018 IEEE MTT-S International Conference on Numerical Electromagnetic and Multiphysics Modeling and Optimization (NEMO)
Fig. 6. Photo of Y-shape filter setup [7].
|
0 |
MS1 |
|
|
M1L |
|
|
|
|
|
|
R1 |
|
|
|
|
|
||
[dB] |
−10 |
S |
MSL |
L |
|
|
|
||
R2 |
|
|
|
|
|
||||
−20 |
MS2 |
|
M2L |
|
|
|
|||
S−parameter |
|
|
|
|
|
|
|
|
|
−30 |
|
|
|
|
|
|
|
|
|
−40 |
|
|
|
|
|
|
S11 measurement |
||
|
|
|
|
|
|
S21 measurement |
|||
−50 |
|
|
|
|
|
|
S11 matrix |
||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
S21 matrix |
||
|
|
|
|
|
|
|
|
||
|
|
1.95 |
|
2 |
|
2.05 |
2.1 |
2.15 |
2.2 |
|
|
|
|
|
frequency [GHz] |
|
|
||
Fig. 7. Comparison of scattering parameters of measurement (Fig. 6) and extracted transversal coupling matrix shown in inset [7].
|
E6 |
|
|
E1 |
E2 |
|
|
|
|
y |
|
y |
E4 |
|
E5 |
|
E3 |
|
E |
|
|
E3 |
E6 |
5 |
|
|
|
||
E |
E4 |
|
|
E |
1 |
|
|
|
2 |
(a) |
x |
(b) |
|
x |
|
|
|
Fig. 8. Y-shape dielectric dual-mode resonator with additional dielectric ring. Branches 4 to 6 connected to (a) housing, (b) to each other in the center.
tors which have already been given in (5) result – or any linear
combination due to the degeneration 1 = 2. For 3 = 2, |
||||||
~ |
|
T |
p |
|
~ |
|
= [1; 1; 1] |
3 |
|||||
a third eigenvector E3 |
|
= |
is obtained. Since E3 |
|||
does not fulfill the continuity equation (3), it is not a valid solution for the given resonator. Nevertheless, it is a valid solution for the resonators depicted in Fig. 8, where additional dielectric branches are added forming a dielectric ring. Due to the continuity equation (3) applied for each node of these structures, the fields of the branches 4, 5 and 6 are determined from the fields of the branches 1, 2 and 3. Therefore, it is only required to formulate the eigenvalue approach as discussed before for the branches 1, 2 and 3. Hence, in these resonator setups, the third solution E3 focuses and guides the electric field to rotate around the ring, which is formed by the branches 1 to 3, resulting in the well-known T E10 -mode.
IV. COMPLEX EIGENMODES
III. SIMPLE EIGENVALUE APPROACH
Based on the proof from Section II-C (Fig. 5), in [5] and [10] a simple eigenvalue approach has been formulated for generalized dielectric resonators with branches and rotational symmetry. For sure this approach also enables to obtain the eigenmodes for the X-/Y-shape resonator from (4)/(5), respectively. This approach and a modification thereof which reveals complex eigenmodes will be explained in this section.
The rotational symmetry is used to determine the eigenmodes. The approach is based on the formulation of a matrix eigenvalue condition: The unknown values for the fields in the branches of an eigenvalue solution are com-
bined in the branch-vector |
as discussed before. For the Y- |
~ |
T |
shape resonator E = [E1 E2 |
E3] . The rotation by the angle |
+120 /-120 results in the branch-vector E~+ = [E2 E3 E1]T |
|
and ~ 3 1 2 T , respectively. With respect to Fig. 5(a),
E = [E E E ]
the superposition should reobtain the original mode, weighted
by a scalar value : |
|
|
|
" |
|
#; (6) |
||
E |
+E = E ) A E = E |
with A = |
1 1 0 |
|||||
~ + |
~ |
~ |
~ |
~ |
|
|
0 1 1 |
|
|
|
1 0 1 |
|
|||||
which defines an eigenvalue problem for the matrix A. Due to the symmetry of the matrix, real eigenvalues = f1; 1; 2g and real eigenvectors will result. For 1;2 = 1 the eigenvec-
Based on the idea that in electromagnetic theory and practice also circular polarized fields can be utilized, the simple eigenvalue approach from last section can be modified by searching for eigenmodes, which fulfil the rotational symmetry condition for just rotating in one direction without superposing the related negative rotation.
A. Y-shape resonator
For n = 3 with 120 -rotational symmetry this leads to the
formulation |
|
|
with A = " |
0 1 0 |
#; (7) |
||
~ + |
~ |
~ |
~ |
||||
0 0 1 |
|||||||
E |
= E |
) A E = E |
1 0 0 |
||||
The resulting eigenvalues are complex = fe+j120 ; e j120 ; 1g. Likewise, the eigenvectors representing the fields in the branches are complex:
E~1 |
= p |
2e+j120 3; E~ |
2 |
= p |
2e j120 3; E~ |
3 |
= p |
213: (8) |
|||||
|
1 |
|
1 |
|
1 |
|
1 |
|
1 |
1 |
|||
|
|
|
|
4e j120 5 |
|
|
|
|
4e+j120 5 |
|
|
|
415 |
|
3 |
|
3 |
|
3 |
||||||||
Again, ~3 represents the 10 -mode from the modified
E T E
resonators shown in Fig. 8. Note that the branch-vectors ~1=2
E are a complex linear combination of the degenerate modes (5) shown in Fig. 4:
|
|
|
|
2 |
|
p |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|||||
E~1=2 |
= |
p1 |
2 13 |
|
j |
3 |
2 |
13: |
(9) |
|||
2 |
||||||||||||
|
2 3 |
4 |
15 |
|
|
|
|
4 15 |
|
|||
2018 IEEE MTT-S International Conference on Numerical Electromagnetic and Multiphysics Modeling and Optimization (NEMO)
B. X-shape resonator
For n = 4 with 90 -rotational symmetry the same approach leads to the complex eigenvalues = f+j; j; 1; +1g and complex eigenvectors representing the fields in the branches:
E~1 = 1 |
2 |
j3; E~ |
2 = |
1 |
2 j3; E~ |
3 = |
12 13; E~ |
4 = |
1 |
213: |
|||||
|
|
1 |
|
|
|
1 |
|
|
|
6 |
1 |
|
|
1 |
|
2 |
6 j7 |
|
2 |
6 j7 |
|
2 |
17 |
|
2 |
617 |
|||||
|
|
6 |
7 |
|
|
6 |
7 |
|
|
|
6 |
7 |
|
|
6 7 |
|
|
1 |
|
|
4 |
1 |
|
|
|
4 |
1 |
|
|
1 |
|
|
|
4 |
5 |
|
|
5 |
|
|
|
5 |
|
|
4 5 |
||
|
E3 |
|
|
|
E8 |
|
|
E3 |
|
|
|
|
E4 |
E |
|
E4 |
|
y |
7 |
|
|
|
|
E2 |
y |
|
|
|
|
|
|
|
|
E |
|
|
|
E2 |
|
|
9 |
|
|
|
|
|
|
|
E5 |
E6 |
|
|
E5 |
|
|
E1 |
|
||
|
E |
|
|
E |
|
|
1 |
|
|
|
|
|
|
|
|
|
10 |
(a) |
x |
(b) |
|
|
x |
|
|
|
|
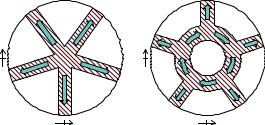
(10)Fig. 9. Examples of 72 -rotational symmetric dielectric multi-branch resonators (a) without, (b) with additional dielectric ring.
C. Discussion
As intended from the approach and can be concluded from
(8) – and (10) with j = ej90 – it is proven, that the modes can be interpreted as being circularly polarized. Furthermore, the complex eigenmodes show the benefit of having same magnitude in all branches. This might be a useful hint for proper design of bandpass filters and control of transmission zeros. Nevertheless, further investigations are required to properly control the phase excitation of the degenerate modes, which to the best knowledge of the authors has not been considered before in filter design procedures. Complex eigenvectors (8) with 120 phase offset are only known for the scattering matrix calculation of ideal junction circulators [11]. In contrast, the coupling matrix filter design leads to coupling values which are either inductive or capacitive (positive or negative coupling). Phase shifter sections – which are basically known in filter theory e.g. for the extracted pole filter synthesis [12] – are required to be included to change the excitation and physical interpretation from horizontal/vertical or diagonal polarized modes to circular polarized modes.
D. Further example
Note that this approach can also be applied for more complex resonators, for example n = 5 with 72 -rotational symmetry. The related geometry of the dielectric resonator with branches is shown in Fig. 9. The complex eigenvalue approach leads to the solution = fej72 ; e j72 ; ej144 ; e j144 ; +1g and complex eigenvectors representing the fields in the branches:
~ |
1 |
2e jj144 3 |
~ |
1 |
2e j288 3 |
~ |
1 |
213 |
||||||
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
E1;2 |
= p5 |
|
72 |
|
= p5 |
|
j144 |
7; E5 |
= p5 |
617: |
||||
6e j216 7; E3;4 |
6e j72 |
|||||||||||||
|
|
|
6e |
7 |
|
|
|
6e |
7 |
|
|
|
6 7 |
|
|
|
|
6 |
j288 7 |
|
|
|
6 |
j216 7 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
617 |
|||||
|
|
|
6e |
7 |
|
|
|
6e |
|
7 |
|
|
|
6 7 |
|
|
|
4 |
5 |
|
|
|
4 |
|
5 |
|
|
|
4 5 |
(11) This solution reveals the presence of a second pair of dualmode resonances. The two different pairs have different rotation angles - as can also be deduced from the complex eigenvalues: For the first pair the field between adjacent branches changes by 72 , while it changes by 144 for the second pair. Note that the related real eigenvectors from the simple approach discussed in Section III have already been shown in [5] for n = 5 and in [13] moreover for n = 8 with 45 -rotational symmetry.
V. CONCLUSION
In this paper, concepts for dielectric dual-mode resonators were reviewed. Besides the mirror symmetry also rotational symmetry of the physical structure can be taken into account to explain degeneration of modes with a simple eigenmode approach. Based on this concept, the performance of X- and Y-shape dielectric resonators were explained. An alternative solution leading to complex eigenmodes was presented for the first time. The resulting modes can be interpreted as circular polarized modes, which gives more insight into the structure and might lead to novel concepts for bandpass filter design.
Furthermore, note that the interpretation is also applicable without considering the dielectric branch concept. Circular polarized modes might also be used for interpretation of dualmode resonators build from circular or square waveguides. Note that they – or more specifically: the concept of oppositely traveling wave resonance modes – had already been applied for circular resonators [14], but only to motivate the modelling of the resonators as a ring transmission line.
REFERENCES
[1]Y. Kobayashi, S. Yoshida, ”Bandpass filters using TM010 dielectric rod resonators,” in Proc. IEEE MTT-Symposium, Otawa, Canada, June 1978.
[2]S. Amari, M. Bekheit, ”Physical interpretation and implications of similarity transformations in coupled resonator filter design,” IEEE Trans. MTT., vol. 55, no. 6, Jun. 2007.
[3]S. Amari, ”Application of representation Theory to dual-mode microwave bandpass filters,” IEEE Trans. MTT., vol. 57, no. 2, Feb. 2009.
[4]Ke-Li Wu, ”An optimal circular-waveguide dual-mode filter without tuning screws,” IEEE Trans. MTT., vol. 47, no. 3, Mar. 1999.
[5]M. Hoft,¨ ”New concepts for dielectric multi-mode resonators with branches,” Proc. IEEE MTT-Symposium, 2008.
[6]M. Hoft,¨ ”Dielectric multi-mode resonator (Y-shape),” European Patent Appl. EP1962371A1, Feb. 21, 2007.
[7]M. Hoft,¨ ”Y-Shape dielectric dual-mode resonator,” IEEE Trans. Microwave Theory Tech., vol. 56, no. 12, Dec. 2008.
[8]G. Conciauro, M. Guglielmi, R. Sorrentino, Advanced Modal AnalysisCAD Tech. for Waveguide Comp. and Filters, New York: Wiley, 2000.
[9]T. Kurisu, S. Abe, ”Multi-mode dielectric resonator and method of adjusting charact. of the res.,” US Patent No. 6,278,344, Aug. 21, 2001.
[10]M. Hoft,¨ ”Hybrid TE/TM-multi-mode resonators,” Proc. German Microwave Conference, Munich, Germany, Mar. 2009.
[11]J. Helszajn, Microwave Engineering: Passive, Active and NonReciprocal Circuits, London: McGraw-Hill, 1992.
[12]R. J. Cameron, R. Mansour, C. M. Kudsia Microwave Filters for Communication Systems, New Jersey: Wiley, 2007.
[13]M. Hoft,¨ ”Dielectric multi-mode resonator,” European Patent Appl. EP1962370A1, Feb. 21, 2007.
[14]I. Awai, T. Yamashita, ”Theory on a circular dual-mode resonator and filter with internal coupling scheme,” Proc. Asia-Pacific Microwave Conference, Hong Kong, Dec. 1997.
