диафрагмированные волноводные фильтры / b8db9692-0df0-4aec-95ce-db0e2a2d8881

Abstract—This paper presents an algorithm for the wide-band optimization of - and -plane waveguide components with irregular shapes. The algorithm is based on the boundary-inte- gral–resonant-mode expansion method, used in conjunction with a variational technique, which permits the determination of the objective function and of its gradient by solving a single electromagnetic problem. The same technique allows for performing a sensitivity analysis to check the effect of the mechanical tolerances on the performance of the component and to estimate the yield for a given manufacturing technology on a large-scale production. Many examples demonstrate the effectiveness of the proposed algorithm.

Index Terms—Optimization methods, sensitivity, tolerance analysis, waveguide components, yield estimation.

I. INTRODUCTION

WAVEGUIDE components with irregular shapes are widely used in aerospace applications since they permit the reduction in weight and size of microwave circuits. Their

design requires efficient computer-aided design (CAD) tools, which combine fast electromagnetic solvers for arbitrary shapes and powerful optimization routines.

Many different methods have been proposed for the analysis of both twoand three-dimensional structures: they are based on integral-equation (IE) techniques, finite-element methods (FEMs), time-domain (TD) approaches, or combinations of different methods (hybrid techniques). Sometimes the segmentation technique can be useful for reducing large and complicated components to simpler ones. Sophisticated optimization techniques have been also developed in the last decade: among them, the space-mapping technique [1]–[3], adjoint network method [4], [5], and semianalytical techniques [6]. In any case, they requires the calculation of the frequency responses of a number of components with slightly different shapes with the aim of minimizing a cost function. To this end, most of them also require the calculation of the sensitivity of the frequency response with respect to geometrical perturbations.

Manuscript received December 24, 2002; revised May 24, 2003. This work was supported in part by the European Commission under the Research and Training Networks Programme under Contract HPRN-CT-2000-00043 and by the University of Pavia under FAR funding.

The authors are with the Department of Electronics, University of Pavia, I-27100 Pavia, Italy (e-mail: arcioni@unipv.it; bozzi@ele.unipv.it; bressan@unipv.it; conciauro@unipv.it; perregrini@unipv.it).

Digital Object Identifier 10.1109/TMTT.2003.820888

Besides the design problems, technological issues also need to be addressed [7]–[9]. In particular, for a small-scale produc- tion—as in the case of space components—the problem is the choice of the manufacturing process, which provides enough accuracy in term of mechanical tolerances. On the contrary, in the case of a large-scale production, the aim is to use a low-cost manufacturing process that guarantees a reasonable yield. In both cases, an estimation of the effect of a lot of random geometrical perturbation is required.

Therefore, either the optimization procedure, tolerance analysis, and yield estimation requires the analysis of a large number of structures with slightly different geometries.

The boundary-integral–resonant-mode expansion (BI–RME) method [10] is particularly well suited for implementation in fast CAD tools devoted to the said tasks, thanks to its high efficiency and to the possibility of using by-products of the analysis for estimating the sensitivity.

Basically, the BI–RME method is a very fast procedure for the solution of eigenvalue problems encountered in microwave theory. In the application to the analysis of waveguide components, the method is used to find a large number of poles and residues of the admittance matrix, thus permitting to obtain, in a short time, the mathematical model of the component, valid over a wide frequency band.

Albeit the method can be used in the analysis of three-dimen- sional (3-D) components with unimodal or multimodal ports [10]–[12], its rapidity is really outstanding in the analysis of -and -plane components in rectangular waveguide with unimodal ports [10], [13], [14]. For this reason, the method has been implemented in a CAD tool especially devoted to the optimized design of this kind of components [15].

A preliminary description of the optimization algorithm has been presented in previous conference papers [16], [17]. In this paper, we give a comprehensive description of the perturbation method used in the optimization algorithm and in the tolerance/yield analysis. Some examples highlight the efficiency of the method and show how the BI–RME method permits to obtain an optimized design in really short times.

II. POLE EXPANSION OF THE 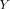-MATRIX

In this section, we give an overview of the application of the BI–RME method to the analysis of -/-plane components, mainly to introduce the basic assumptions, concepts, and the

Fig. 1. Example of planar waveguide components. (a) H-plane component.

(b) E-plane component.

Fig. 2. Cross section of the cylindrical cavity obtained by closing the ports of the H-plane component of Fig. 1(a).

Fig. 3. Domain S is embedded in an external rectangular domain for the application of the BI–RME method.

symbols involved in the theory to follow. The formulas are justified in [13] and [14]. A comprehensive discussion can be found in [10, Chs. 5 and 6].

Considering a generic - or -plane waveguide component (Fig. 1) with unimodal ports filled with a homogeneous, isotropic, and lossless medium, the BI–RME method leads to the calculation of the coefficients involved in the following approximate pole expansion of the admittance matrix:

in

where is the cross section of the cavity and is its boundary (Fig. 2). The resonant wavenumbers are

Fig. 4. Arbitrary deformation of the polygonal line that represent the boundary

@S.

the evaluation of the variation of the quantities , , ,

the widths or of the terminal waveguides, which are normally fixed quantities. Therefore, and are not involved in the optimization. Thus, the following discussion is concen-

By using a well-known procedure (see, for instance, [18]), the eigensolutions of the Helmoltz equation in the domain can be obtained by minimizing the variational functional

(10)

where denotes the trial function and

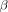
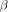
in the case of Dirichelet b.c.in the case of Neumann b.c.

Equation (10) is often used to find the perturbation of each eigenfunction by considering as trial function the corresponding unperturbed eigenfunction. This procedure is justified only if the resonant frequencies are well spaced one from each other because, otherwise, the perturbation results into eigenfunction coupling. In our case, we have to consider many higher order eigenfunctions whose eigenvalues change unpredictably during the optimization procedure. As a consequence, having quasi-de- generate eigenfunctions is far from being unlike, and eigenfunc- tion-coupling is often important. Therefore, a more general class of trial functions must be used, given by a combination of the unperturbed eigenfunctions

Note that the definition of the eigenfunction is extended outside

by analytic continuation in order to define in the whole domain , and also in cases where a part of the perturbed domain is outside .

It should be noted that the perturbation of the highest order eigenfunctions (say, ) is less accurate than the perturbation of the other eigenfunctions because their coupling is considered only with lower eigenfunctions. This, however, is not a problem since the highest poles in (1) are well above the maximum frequency of interest, and the accuracy in their perturbation is unimportant

On substitution of (11) or (12) into (10), we obtain

(13)

(14)

where and are the vectors of the weights and the matrices

, , , and are defined as

(15)

(16)

(17)

(18)

In the practical implementation of the BI–RME method, the line is represented by one or more polygonal lines so that the whole boundary consists of one or more polygonals (Fig. 4). For notational simplicity, we assume that is simply connected so that is a single line (the extension to more lines is straightforward). Denoting by the number of vertices, the most general perturbation is represented by some displacements 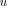, where and are the unit vectors along and , respectively, and and are small distances. It is easily realized that the displacement of a generic point of the boundary (see Fig. 4) is given by

(19)

where is a coordinate taken on corresponding to the said point, and and are the coordinates of the vertices placed just before and after (note that the vertex before the first or after the th one are labeled by and 1, respectively). As shown in Appendix A, we have (to first order in the - and -pa- rameters)

322

TABLE I

QUANTITIES INVOLVED IN THE CALCULATION OF

IEEE TRANSACTIONS ON MICROWAVE THEORY AND TECHNIQUES, VOL. 52, NO. 1, JANUARY 2004

-plane

MATRICES T, T , AND V

(28)

(29)

IV. ERROR FUNCTION AND OPTIMIZATION VARIABLES

The optimization of the frequency response of a component requires to fulfill at the same time many different goals, which (21) are usually defined as required values of amplitudes and/or phases of the scattering parameters or as a prescribed group

(22)delay, at many different frequencies.

where , , and are defined in Table I. In most cases, the perturbation is performed in the line , where the values of or are obtained directly from the BI–RME algorithm in the form of a linear combination of splines. In this case, the integrals in Table I become a linear combination of integrals evaluated analytically and involving the same coefficients provided by the algorithm. This is a nonnegligible advantage deriving from the use of the BI–RME al-

gorithm.

By applying the Rayleigh–Ritz method to find the stationary value of (13) and (14) (i.e., enforcing ), we obtain the following generalized linear eigenvalue equations:

(24)

(25)

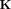
where , , and is the identity matrix.

By solving these equations, we find the perturbed eigenvalues of (4) and (5). The eigenvectors (primed or double primed) give the weights to be inserted into (11) and (12) to obtain the perturbed eigenfunctions. On substitution of the perturbed eigenvalues and eigenfunctions into (6)–(9), we finally obtain the following perturbed quantities.

quantity must assume the required values . The optimization is carried out by modifying some optimization variables (discussed below) in such a way as to minimize an “error function,” which, for instance, can be defined as

(30) where is the actual value of the th quantity at and is a weighting coefficient. Many other definitions can be used for more complicated conditions such as the requirement for a maximum or minimum value of a quantity, a flat frequency behavior, a fixed difference between two quantities, etc.

In principle, the optimization variables could coincide with the displacements and 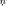of all the vertices of . This choice, however, results in an excessive number of variables and, above all, it does not allow for any control of the deformation of the boundary, possibly leading to odd shapes. Actually, in practical implementation of the optimization algorithm, it is convenient to define some “elementary deformations” (EDs), consisting of the translation of a group of adjacent vertices in a prescribed direction. Each ED is associated to an optimization variable. For instance, Fig. 5 shows the result of three subsequent EDs, namely,

for otherwise

for otherwise

for otherwise

Fig. 5. Example of controlled reshaping of a portion of @S, obtained by combining three subsequent EDs.

at the points where some degeneracy occurs between eigenfunctions (see Appendix B). Therefore, a gradient-based method can be used for the optimization.

Such a method requires the numerical calculation of the derivatives . This calculation, however, is not time consuming since the increment of is obtained after having determined the perturbed scattering parameters, which, in turn, are deduced from (1) on substitution of and corresponding to each ED.

V. TOLERANCE ANALYSIS

The variational approach is also useful for the tolerance analysis of the optimized component. Two kinds of results can be obtained, which are: 1) a sensitivity map, which identifies the parts of the profile whose displacements most critically affect the frequency response and 2) an estimation of the range of variation of the scattering parameters for given mechanical tolerances. In both cases, the analysis requires to define many EDs that represent expected inaccuracies due to the manufacturing process (e.g., a shift in the position of a sidewall, an error in the radius of a rounding, etc.).

To obtain a sensitivity map, we consider the response of the optimized component to define the goals to which the error function is referred, and then we calculate for a small displacement of all EDs, thus obtaining the sensitivities of with respect to each ED, i.e., the sensitivity map. The minimum value of the tolerance allowed by the manufacturing process can be required in the most sensitive parts of the component, whereas relaxed mechanical tolerance can be set elsewhere.

Once the mechanical tolerances have been set, the range of variation of the scattering parameters can be estimated through a Monte Carlo analysis. We consider a large number of components, which differ from the optimized one by random values (within the assigned tolerance limits) of the EDs representing the manufacturing inaccuracies. The displacements and

of the th vertex are then calculated by summing up those of all

Fig. 6. Cross section of the X-band H-plane filter. The arrows indicate the five EDs used in the optimization. All dimensions are in millimeters.

the EDs. Hence, by solving (24) or (25), we obtain quantities

and and, therefore, the frequency behavior. By plotting the responses of all the perturbed components, we obtain the expected spread area.

It is worth observing that, due to the small dimension of the eigenvalue problems (24) and (25), the Monte Carlo analysis performed by the perturbation procedure is much faster than the determination of a new mathematical model.

VI. YIELD ESTIMATION

The yield of a large-scale manufacturing process is determined by defining the spread in the performance of acceptable products. Its value is estimated by a Monte Carlo analysis carried out on the frequency responses of a lot of components, randomly deformed with respect to the optimized shape, according to the tolerances of the selected manufacturing process. Therefore, the yield estimation also requires repeated analysis of hundreds or sometime thousands of slightly different components.

In our approach, the variational technique permits to obtain the yield analysis in a very short time since it requires only the analysis of one component and many solutions of the small eigenvalue problems (24) or (25).

VII. RESULTS

In this section, we present the design of some components obtained by the code ANAPLAN-W [15]. This code implements the analysis of -/-plane components, based on the BI–RME method [13], [14], as well as the optimization procedure described in this paper. ANAPLAN-W is provided with a graphical interface that permits to easily draw the cross section transform it into a polygonal and define the EDs. The goals for the optimization are defined writing a simple text file and they are automatically converted into a procedure for evaluating the error function .

The first example refers to the optimization of an 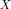-band -plane filter. The cross section of the filter is shown in Fig. 6. The goals were an insertion loss 2 dB in the band 9.5 10.5 GHz and 30 dB below 9.3 GHz and above 10.8 GHz. The starting point of the optimization was a folded

Fig. 7. Evolution of the frequency response of the filter of Fig. 6 during the optimization process.

TABLE II

YIELD ESTIMATION FOR THE FIVE-CAVITY FILTER OF FIG. 6, CONSIDERING

DIFFERENT MECHANICAL STANDARDS

structure consisting of five rectangular cavities, all resonating at approximately 10 GHz, coupled through arbitrarily chosen apertures. The analysis was performed by considering , thus retaining terms in the summation appearing in

(1). The initial response (see Fig. 7) was far away from the prescribed goals. The symmetry of the structure was exploited to speed up the analysis and simplify the optimization, and the EDs indicated by thick lines and arrows in Fig. 6 were considered. These EDs are very effective in tuning the resonance frequencies of the cavities, as well as their coupling. The goals were fulfilled after 42 optimization steps (Fig. 7) and the CPU time per step was 3 s using a Sun Ultra 10 workstation.

For this filter, we also estimated the yield of a large-scale production. Table II shows the results obtained in the case of two different mechanical standards [20] with a zero-mean Gaussian distribution of the displacement of the vertices of the polygonal that describe the component sidewalls. The tolerance (i.e., the maximum expected displacement) is approximately six times the standard deviation. These results were obtained in 34 s by considering 500 components. To verify the reliability of the perturbation approach, we also made the same estimation calculating the frequency response of all the components without using the perturbation technique. The results in term of percentage were exactly the same, but the computing time raised to 27 min. Finally, to verify the convergence of the Monte Carlo

Fig. 8. 3-D view and cross section of an E-plane 3-dB coupler. The arrows indicate the three EDs used in the optimization. All dimensions are in millimeters.

analysis, we increased the number of simulated components up to 5000. No significant changes were observed.

As a second example, we report the complete design of the WR-22 -plane 3-dB power splitter shown in Fig. 8(a). The design specification was a coupling coefficient of 3 0.5 dB in the 42 48 GHz frequency band. The analysis was performed by considering , which leads to . The optimization was performed displacing the three EDs shown in Fig. 8(b) (taking into account the two symmetry planes, only one-fourth of the structure had to be considered). The whole optimization process required only 30 steps and the total computing time was only 60 s. The calculated response of the optimized component is reported in Fig. 9 (black lines). The manufacturing process allowed for a mechanical tolerance value of 15 m, and the estimated variations of the response resulted within the design specification, as shown by the upper and lower bounds of Fig. 9. Note that the complete sensitivity analysis required only 2 min: 20 s were spent to perform the analysis (without exploiting the symmetries) of the component with nominal dimensions, and only 100 s were sufficient to obtain (by using the variational approach described in Section III) the statistical sample of 1000 frequency responses of components with dimensions varied within the 15 m tolerance. The calculated response is in good agreement with the experimental one, as shown in Fig. 9 (gray lines). The values of the measured coupling coefficients [see Fig. 9(b) and (c)] differ slightly from the computed ones due to the junction losses not considered in the analysis.

The last example is the design of a nine cavity -plane filter with an unusual “meander shape.” The filter was designed with standard WR-34 waveguide ports, and its particular shape permits the coupling of the cavities through high-order modes of the waveguide, thus providing the implementation of transmission zeros close to the passband of the filter [19]. The goals were a return loss 18 dB in the band 24.7 27.7 GHz and an insertion loss 50 dB below 24 GHz and above 28.8 GHz.

Fig. 9. Comparison between computed and measured results for the E-plane coupler of Fig. 8. The region between the lower and upper bounds represents the expected spread area when considering a tolerance of 615 m.

The filter (whose geometry is shown in Fig. 10) has been manufactured and measured. The measured frequency response is shown in Fig. 11. Furthermore, the tolerance analysis has been performed and Fig. 11(b) shows the expected spread area (shadowed region) for , assuming a tolerance of 25 m on the dimensions of the cavities. The analysis of the filter required 15 s (, ) and the tolerance analysis took 1 min (statistical sample: 1000 cases).

Fig. 11. Measured results for the filter of Fig. 10. The shadowed region represents the expected spread area when considering a tolerance of 625 m.

VIII. CONCLUSIONS

In this paper, we presented a powerful gradient-based algorithm for the optimized design of waveguide components. This algorithm is based on the representation of the admittance matrix in the form of a pole-expansion in the frequency domain. A perturbational approach was used for evaluating the effect of small deformations of the geometry of the component on

poles and residues. This formulation holds true even in the case of clusters of poles, where the perturbation may cause abrupt changes in the residues. The use of this algorithm in conjunction with the BI–RME method permitted to obtain a very efficient CAD tool able to perform the automatic optimization of unconventional components in tens of seconds on a standard PC.

Moreover, the same perturbational approach, in conjunction with Monte Carlo method, was implemented in a code for the tolerance and yield analysis of large-scale productions. By using this code, the frequency responses of thousands of slightly different components are usually obtained in less than 1 min.

APPENDIX A

A. Derivation of (20)–(23)

By using the first Green’s identity

(A.1)

and the relationship , (15) becomes

(A.2)

Since the surface differs slightly from , we can write

(A.3)

where is a generic scalar function defined on , is the position vector in , and is the outward normal on . Due to (19), the line integral on the right-hand side (RHS) approximate to the first order in the - and -parameters the surface integral over .

By using (A.3) and recalling the normalization

and the boundary condition on , from (A.2), we obtain

(A.4)

By applying (A.1) to the surface integral on , taking into account the boundary condition and the Helmoltz equation, (A.4) becomes

By rearranging the summations and using the cycling rules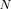

and for the subscripts (which holds true due to the hypothesis that is a single polygonal line), we prove (20).

To prove (15), we split the integral by using (A.3) and apply (A.1) as follows:

(A.6)

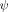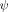
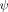
Due to the boundary condition satisfied by , the first integral vanishes and reduces to the only component along . Moreover, . Therefore, taking into account that , (A.6) becomes

(A.7)

By applying the same procedure used to obtain (A.5), the integral can be written as a sum of integrals on the segments that represent the boundary. By substituting (19) and rearranging the integrals, we obtain (21).

Equation (22) is easily proven by using (A.3) and taking into account that and that on .

In a similar way, we can prove (23) by using (A.3) and applying the same procedure used to obtain (A.5).

where , , and are obtained using (6) and (8). Since the eigenfunctions are degenerate, an infinitesimal perturbation gives rise to an abrupt change of the eigensolutions, which became [21]

where depends on the perturbation. As a consequence, due to (8), we have

In conclusion, (A.8) is not affected by the discontinuity of the eigenfunctions. This implies that the scattering parameters varies continuously with the deformation in spite of the possible discontinuity of the eigenfunctions.

A similar reasoning applies in the case of -plane components.

REFERENCES

[1]J. W. Bandler, R. M. Biernacki, P. A. Grobelny, R. H. Hemmers, and S. H. Chen, “Space mapping technique for electromagnetic optimization,” IEEE Trans. Microwave Theory Tech., vol. 42, pp. 2536–2544, May 1994.

[2]J. W. Bandler, R. M. Biernacki, L. W. Hendrick, D. Omeragic, and S. H. Chen, “Electromagnetic optimization of 3-D structures,” IEEE Trans. Microwave Theory Tech., vol. 45, pp. 770–779, May 1997.

[3]M. H. Bakr, J. W. Bandler, N. Georgieva, and K. Madsen, “A hybrid aggressive space-mapping algorithm for EM optimization,” IEEE Trans. Microwave Theory Tech., vol. 47, pp. 2440–2449, Dec. 1999.

[4]F. Alessandri, M. Mongiardo, and R. Sorrentino, “New efficient full wave optimization of microwave circuits by the adjoint network method,” IEEE Microwave Guided Wave Lett., vol. 3, pp. 414–416, Nov. 1993.

[5]F. Alessandri, M. Dionigi, and R. Sorrentino, “A fullwave CAD tool for waveguide components using a high speed direct optimizer,” IEEE Trans. Microwave Theory Tech., vol. 43, pp. 2046–2052, Sept. 1995.

[6]P. Harscher, S. Amari, and R. Vahldieck, “A fast finite-element-based field optimizer using analytically calculated gradients,” IEEE Trans. Microwave Theory Tech., vol. 50, pp. 433–439, Feb. 2002.

[7]A. E. Atia, X. P. Liang, and K. A. Zaki, “Channel expansion and tolerance analysis of waveguide manifold multiplexers,” IEEE Trans. Microwave Theory Tech., vol. 40, pp. 1591–1594, July 1992.

[8]M. Mongiardo and R. Ravanelli, “Automated design of corrugated feeds by the adjoint network method,” IEEE Trans. Microwave Theory Tech., vol. 45, pp. 787–793, May 1997.

[9]P. Harscher and R. Vahldieck, “Automated computer-controlled tuning of waveguide filters using adaptive network models,” IEEE Trans. Microwave Theory Tech., vol. 49, pp. 2125–2130, Nov. 2001.

[10]G. Conciauro, M. Guglielmi, and R. Sorrentino, Advanced Modal Analysis: Wiley, 2000, ch. 5 and 6.

[11]P. Arcioni, M. Bozzi, M. Bressan, and L. Perregrini, “A novel CAD tool for the wideband modeling of 3D waveguide components,” Int. J. RF Microwave Computer-Aided Eng., vol. 10, pp. 183–189, May 2000.

[12]P. Arcioni, M. Bozzi, M. Bressan, G. Conciauro, and L. Perregrini, “Frequency/time-domain modeling of 3D waveguide structures by a BI–RME approach,” Int. J. Numer. Modeling, vol. 15, no. 1, pp. 3–21, Jan. 2002.

[13]G. Conciauro, P. Arcioni, M. Bressan, and L. Perregrini, “Wideband modeling of arbitrarily shaped H-plane waveguide junctions by the boundary integral-resonant mode expansion’ method,” IEEE Trans. Microwave Theory Tech., vol. 44, pp. 1057–1066, July 1996.

[14]P. Arcioni, M. Bressan, G. Conciauro, and L. Perregrini, “Wideband modeling of arbitrarily shaped E-plane waveguide junctions by the boundary integral-resonant mode expansion’ method,” IEEE Trans. Microwave Theory Tech., vol. 44, pp. 2083–2092, Nov. 1996.

[15]P. Arcioni, M. Bressan, G. Conciauro, L. Perregrini, and G. Gatti, “ANAPLAN-W: A CAD tool for E/H-plane waveguide circuits,”

ESA—Preparing for the Future, vol. 6, pp. 12–13, Mar. 1996.

[16]P. Arcioni, L. Perregrini, and P. Arpesi, “Optimization and tolerance analysis of planar waveguide components,” in Proc. 28th Eur. Microwave Conf., Amsterdam, The Netherlands, Oct. 5–9, 1998, pp. 220–225.

[17]P. Arcioni, M. Bozzi, M. Bressan, G. Conciauro, and L. Perregrini, “Optimized design and tolerance analysis of waveguide components by the BIRME method,” presented at the IEEE MTT-S Int. Microwave Symp. Workshop, Boston, MA, June 11–16, 2000.

[18]J. B. Davies, “The finite element method,” in Numerical Techniques for Microwave and Millimeter Wave Passive Structures, T. Itoh, Ed. New York: Wiley, 1989, ch. 2.

[19]M. Guglielmi, F. Montauti, L. Perregrini, and P. Arcioni, “Implementing transmission zeros in inductive-window bandpass filters,” IEEE Trans. Microwave Theory Tech., vol. 43, pp. 1911–1915, Aug. 1995.

[20]“ISO System of Limits and Fits—Part 1: Bases of Tolerances, Deviations and Fits,” Int. Org. Standardization, Geneva, Switzerland, Doc. ISO 286-1, Jan. 1988.

[21]R. Muller, “Theory of cavity resonators,” in Electromagnetic Waveguides and Cavities, G. Goubeau, Ed. New York: Pergamon, 1961, ch. 2.

Paolo Arcioni (M’90–SM’03) was born in Busto Arsizio, Italy, in 1949. He received the Laurea degree in electronic engineering from the University of Pavia, Pavia, Italy, in 1973.

In 1974, he joined the Department of Electronics, University of Pavia, where he currently teaches a course in microwave theory as a Full Professor. In 1991, he was a Visiting Scientist with the Stanford Linear Accelerator Center, Stanford, CA, where he has worked in cooperation with the RF Group to design optimized cavities for the PEP II Project.

From 1992 to 1993, he collaborated with the Istituto Nazionale de Fisica Nucleare (INFN), Frascati, Italy, with the design of accelerating cavities for the DA8NE storage ring. His main research interests are in the area of microwave theory, modeling, and design of interaction structures for particle accelerators and development of numerical methods for the electromagnetic CAD of passive microwave components. His current research activities concern the modeling of planar components on semiconductor substrates and of integrated structures for millimeter-wave circuits.

Prof. Arcioni is a member of the Editorial Board of the IEEE TRANSACTIONS ON MICROWAVE THEORY AND TECHNIQUES.

Maurizio Bozzi (S’98–M’01) was born in Voghera, Italy, on June 1, 1971. He received the Laurea degree in electronic engineering and the Ph.D. in electronics and computer science from the University of Pavia, Pavia, Italy, in 1996 and 2000, respectively.

From December 1996 to September 1997, he was a Guest Researcher with the Technical University of Darmstadt, Darmstadt, Germany. From October 2001 to January 2002, he was a Post-Doctoral Fellow with the University of Valencia, Valencia, Spain. From November to December 2002, he was

an Invited Professor with the Polytechnical University of Montreal, Montreal, QC, Canada. Since March 2002, he has been an Assistant Professor of electromagnetics with the Department of Electronics, University of Pavia. His main research activities concern the electromagnetic modeling of frequency-se- lective surfaces, waveguide components, and microwave printed and integrated circuits.

Dr. Bozzi received the Best Young Scientist Paper Award at the XXVII General Assembly of URSI (International Union of Radio Science) in 2002, and the MECSA Prize for the best paper presented by a young researcher at the Italian Conference on Electromagnetics (XIII RINEM) in 2000.

Marco Bressan (M’94) was born in Venice, Italy, in 1949. He received the Laurea degree in electronic engineering from the University of Pavia, Pavia, Italy, in 1972.

Since 1973, he has been with the Department of Electronics, University of Pavia, as a Researcher in electromagnetics. In 1987, he joined the faculty of engineering, University of Pavia, as an Associate Professor. His research interests include analytical and numerical methods to determine electromagnetic fields for the CAD of passive microwave and

millimeter-wave components.

Prof. Bressan serves on the Editorial Board of the IEEE TRANSACTIONS ON

MICROWAVE THEORY AND TECHNIQUES.

Giuseppe Conciauro (A’72–M’87–SM’03) was born in Palermo, Italy, in 1937. He received the Electrical Engineering and Libera Docenza degrees from the University of Palermo, Palermo, Italy, in 1961 and 1971, respectively.

From 1963 to 1971, he was an Assistant Professor of microwave theory with the Institute of Electrical Engineering, University of Palermo. In 1971, he joined the Department of Electronics, University of Pavia, Pavia, Italy, where he teaches electromagnetic theory as a Full Professor. From 1985 to 1991, he

served as Director of the Department of Electronics and, for many years, he chaired the board of the professors of the graduation course in electrical engineering. He currently chairs the Ph.D. school in electronic, electrical engineering and computer science at the University of Pavia. He authored the textbook Introduzione alle Onde Elettromagnetiche (Milan, Italy: McGraw-Hill Italia, 1992) and coauthored Advanced Modal Analysis (Chichester, U.K.: Wiley, 2000) and Fondamenti di Onde Elettromagnetiche (Milan, Italy: McGraw-Hill Italia, 2003). His main research interests are microwave theory, interaction structures for particle accelerators, and numerical methods in electromagnetics.

Prof. Conciauro serves on the Editorial Board of the IEEE TRANSACTIONS ON

MICROWAVE THEORY AND TECHNIQUES.

Luca Perregrini (M’98) was born in Sondrio, Italy, in 1964. He received the Laurea degree in electronic engineering and Ph.D. degree in electronics and computer science from the University of Pavia, Pavia, Italy, in 1989 and 1993, respectively.

In 1992, he joined the Department of Electronics, University of Pavia, as an Assistant Professor of electromagnetics. He currently teaches courses in electromagnetic field theory and microwave. In 2001 and 2002, he was an Invited Professor with the Polytechnical University of Montreal, Montreal, QC, Canada.

He was a consultant with the European Space Agency and with some European telecommunication companies. He coauthored the textbook Fondamenti di Onde Elettromagnetiche (Milan, Italy: McGraw-Hill Italia, 2003). His main research interests are numerical methods for the analysis and optimization of waveguide circuits, frequency-selective surfaces, reflect arrays, and printed microwave circuits.

Dr. Perregrini serves on the Editorial Board of the IEEE TRANSACTIONS ON MICROWAVE THEORY AND TECHNIQUES and as a reviewer for the IEEE TRANSACTIONS ON ANTENNAS AND PROPAGATION.