МИНОБРНАУКИ РОССИИ

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ

ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

«ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА)

Кафедра математического обеспечения и применения ЭВМ

ОТЧЕТ

по практической работе №3

по дисциплине «Цифровая обработка сигналов»

Тема: Частотный анализ полиномиальных приближений

Студент гр. 0303		Архипов В.А.
Студент гр. 0303		Болкунов В.О.
Студент гр. 0303		Калмак Д.А.
Преподаватель		Середа А.-В.И.

Санкт-Петербург

2023

Цель работы.

Провести анализ частотных характеристик известных формул полиномиального сглаживания временных рядов.

Основные теоретические положения.

Дискретный нерекурсивный фильтр

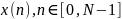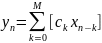Для заданного дискретного сигнала последовательность описывающая выходной сигнал нерекурсивного фильтра в общем случае выглядит следующим образом: , где M - размер окна в котором производится сглаживание.

Передаточная функция

Для дискретного сигнала передаточная функция рекурсивного фильтра 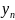вычисляется следующим образом:

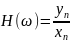
Применяя к данному равенству формулу последовательности выходного сигнала дискретного нерекурсивного фильтра получаем:

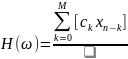
В случае гармонического дискретного сигнала передаточная функция будет иметь следующий вид:

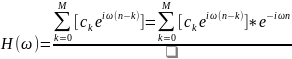
Связь передаточной функции для круговой частоты и циклической.

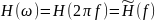
Постановка задачи.

Получить формулы для передаточных функций нерекурсивных фильтров, соответствующих полиномиальному сглаживанию дискретного сигнала для полиномов различного порядка и построить графики 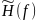. Проинтерпретировать частотные свойства передаточных функций. Провести сопоставительный анализ частотных характеристик передаточных функций для различных степеней полиномов.

Выполнение работы. Сглаживание прямой линией

Выходной сигнал для фильтра сглаживания полиномом 1-ой степени можно записать как:

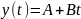
Рассмотрим приближение по трём точкам.

Для нахождения коэффициентов полинома для наилучшего приближения воспользуемся формулой МНК:

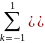
Взяв частные производные по A и B получим следующую систему уравнений

Итого получаем 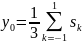или в общем случае

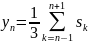
Взяв в качестве входного сигнала некоторый дискретный гармонический сигнал 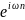получим формулу для выражения передаточной функции.

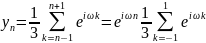
Тогда

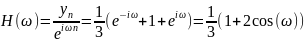
Аналогично выведем формулы выходных сигналов для сглаживания по 5, 7 и 9 точкам соответственно.

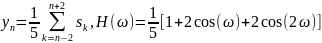
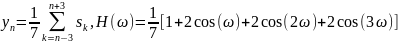
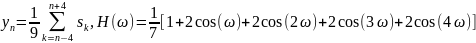
Графики передаточной функции нерекурсивного фильтра, соответствующего сглаживанию прямой линией по 3, 5, 7 и 9 точкам представлены на рис. 1.

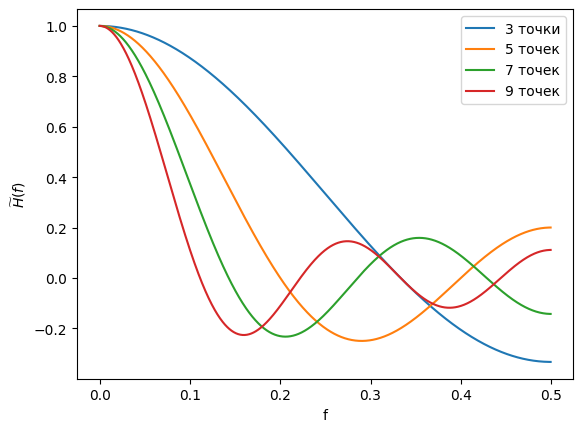
Рисунок 1 - Графики передаточной функции нерекурсивного фильтра, соответствующего сглаживанию прямой линией по 3, 5, 7 и 9 точкам

Как видно из графиков передаточных функций, при увеличении количества точек передаточная функция становится более крутой, то есть быстрее переходит в полосу подавления.

Сглаживание полиномом 2-ой степени

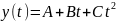
Рассмотрим случай для 13 точек:

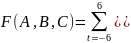
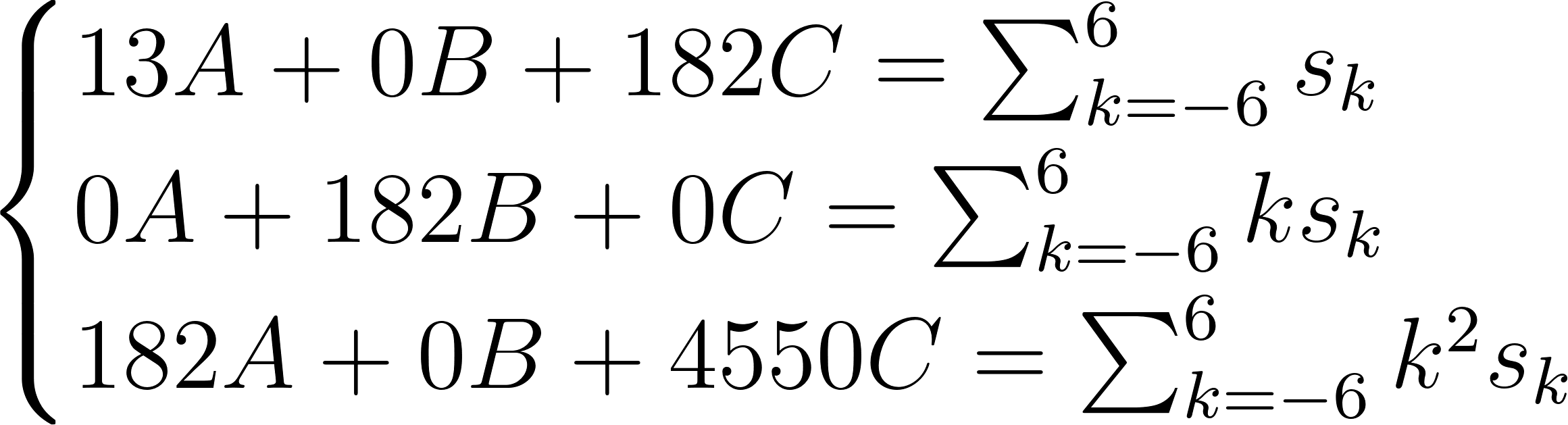
Домножим первое уравнение на 25 и вычтем из него третье:

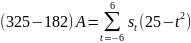
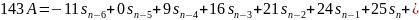
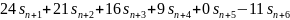
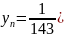
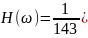
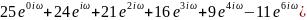
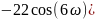
Аналогичными преобразованиями получим и 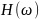для 7, 9, 11 точек соответственно:

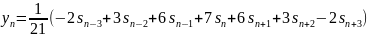
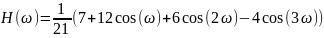
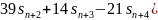
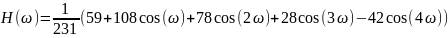
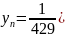
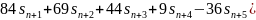
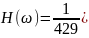
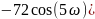
Графики передаточной функции нерекурсивного фильтра, соответствующего сглаживанию полиномом второй степени по 7, 9, 11 и 13 точкам представлены на рис. 2.

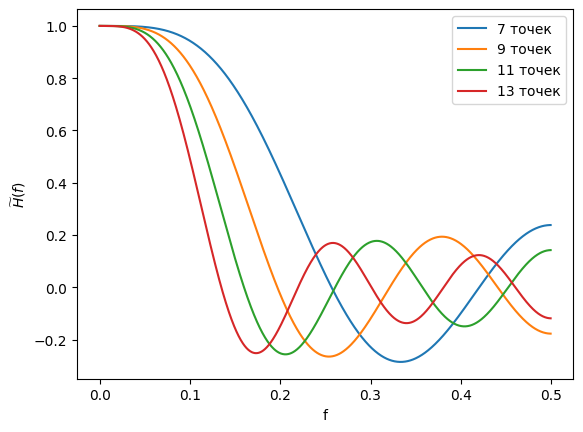
Рисунок 2 - Графики передаточной функции нерекурсивного фильтра, соответствующего сглаживанию полиномом второй степени по 7, 9, 11 и 13 точкам

Из данных графиков можно заметить что как и в случае с приближением прямой линией передаточные функции становятся более крутыми при увеличении количества точек.

Сглаживание полиномом 4-ой степени

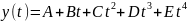
Рассмотрим случай для 9 точек:

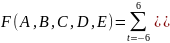
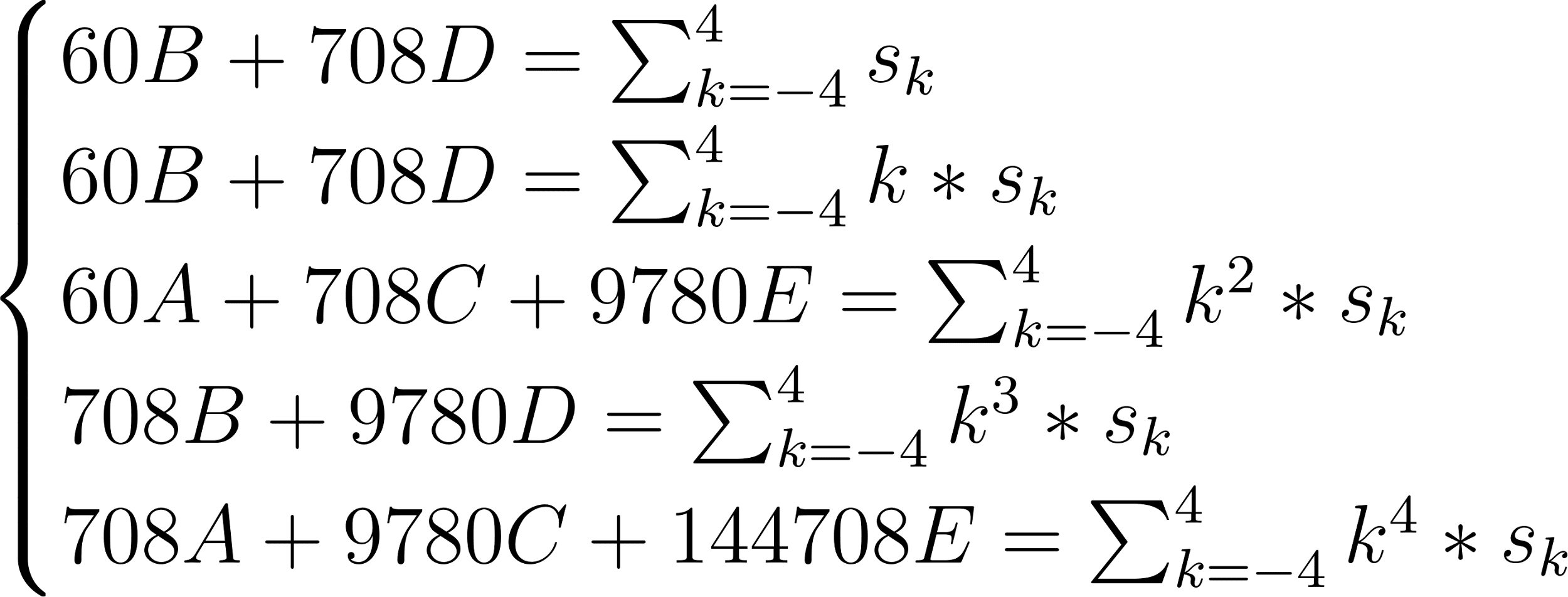
Решив систему уравнений для А, получаем:

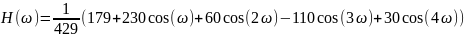
Аналогичными преобразованиями получим и для 11, 13, 15 точек соответственно

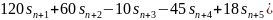
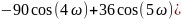
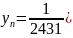
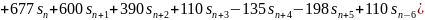
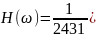
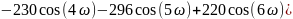
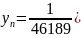
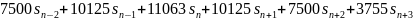
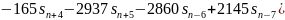
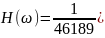
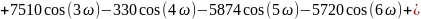
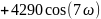
Графики передаточной функции нерекурсивного фильтра, соответствующего сглаживанию полиномом четвёртой степени по 9, 11, 13 и 15 точкам представлены на рис. 3.

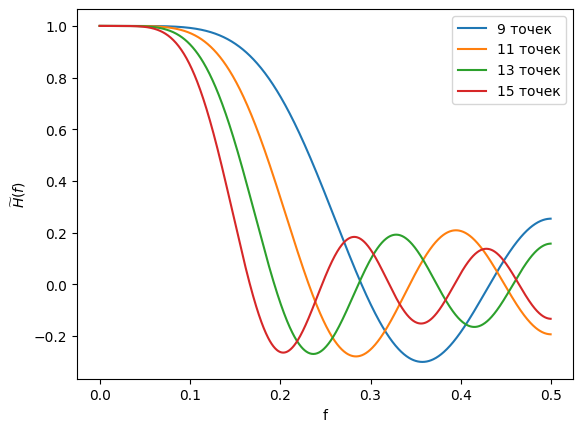
Рисунок 3 - Графики передаточной функции нерекурсивного фильтра, соответствующего сглаживанию полиномом четвёртой степени по 9, 11, 13 и 15 точкам

Аналогично для передаточных функций фильтра приближением полиномом 4-ой степени, можно заметить что при увеличении количества точек функции значительно быстрее приближаются к полосе подавления и начинают колебаться.