1.5.Релятивстская механика.Ч.В

Релятивистская механика

ФОРМУЛЫ

В специальной теории относительности рассматриваются только инерциальные системы отсчета. Во всех задачах считается, что оси y, yʹ и z, zʹ сонаправлены, а относительная скорость ʋ₀ системы координат Kʹ относительно системы K направлена вдоль общей оси xxʹ (рис. 5.1).

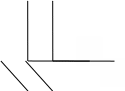
Релятивистское (лоренцево) сокращение длины стержня:

,

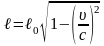здесь ℓ₀ – длина стержня в системе координат Kʹ, относительно которой стержень покоится (собственная длина). Стержень параллелен оси xʹ; ℓ – длина стержня, измеренная в системе K, относительно которой он движется со скоростью ʋ; c – скорость распространения электромагнитного излучения;

Релятивистское замедление хода часов:

,

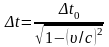здесь Δt₀ – интервал времени между двумя событиями, происходяobми в одной точке системы Kʹ, измеренный по часам этой системы (собственное время движущихся часов); Δt – интервал времени между двумя событиями, измеренный по часам системы K.

Релятивистское сложение скоростей где

,

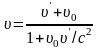здесь ʋʹ – относительная скорость (скорость тела относительно системы Kʹ), ʋ₀ – переносная скорость (скорость системы Kʹ относительно K), ʋ – абсолютная скорость (скорость тела относительно системы K).

В теории относительности абсолютной скоростью называется скорость тела (частицы) в системе координат, условно принятой за неподвижную.

Релятивистская масса:

,

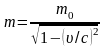здесь m₀ – масса покоя;

Релятивистский импульс:

,

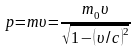Полная энергия релятивистской частицы:

,

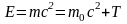здесь T – кинетическая энергия частицы, m₀c² = E₀ – ее энергия покоя. Частица называется релятивистской, если скорость частицы сравнима со скоростью света;

Связь полной энергии с импульсом релятивистской частицы:

;

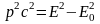Связь кинетической энергии с импульсом релятивистской частицы:

.

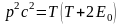Релятивистское изменение длин u интервалов времени

5.1. Предположим, что мы можем измерить длину стержня с точностью Δℓ = 0,1 мкм. При какой относительной скорости и двух инерциальных систем отсчета можно было бы обнаружить релятивистское сокращение длины стержня, собственная длина ℓ₀ которого равна 1 м?

5.2. Двое часов после синхронизации были помещены в начало систем координат K и Kʹ , движущихся относительно друг друга. При какой скорости u их относительного движения возможно обнаружить релятивистское замедление хода часов, если собственная длительность τ₀ измеряемого промежутка времени составляет 1 с? Измерение времени производится с точностью Δτ = 10 пс.

5.3. На космическом корабле-спутнике находятся часы, синхронизированные до полета с земными. Скорость ʋ₀ спутника составляет 7,9 км/с. На сколько отстанут часы на спутнике по измерениям земного наблюдателя по своим часам за время τ₀ = 0,5 года?

5.4. Фотонная ракета движется относительно Земли со скоростью ʋ = 0,6c. Во сколько раз замедлится ход времени в ракете с точки зрения земного наблюдателя?

5.5. В системе Kʹ покоится стержень, собственная длина ℓ₀ которого равна 1 м. Стержень расположен так, что составляет угол φ₀ = 45º с осью xʹ. Определить длину ℓ стержня и угол φ в системе K, если скорость ʋ₀ системы Kʹ относительно K равна 0,8c.

5.6. В системе K находится квадрат, сторона которого параллельна оси xʹ. Определить угол φ между его диагоналями в системе K, если система Kʹ движется относительно K со скоростью ʋ = 0,95c.

5.7. В лабораторной системе отсчета (K-система) пи-мезон с момента рождения до момента распада пролетел расстояние ℓ = 75 м. Скорость ʋ пи-мезона равна 0,995c. Определить собственное время жизни τ₀ пи-мезона.

5.8. Собственное время жизни τ₀ мю-мезона равно 2 мкс. От точки рождения до точки распада в лабораторной системе отсчета мю-мезон пролетел расстояние ℓ = 6 км. С какой скоростью ʋ (в долях скорости света) двигался мезон?

Релятивистское сложение скоростей

5.9. Показать, что формула сложения скоростей релятивистских частиц переходит в соответствующую формулу классической механики при ʋ₀ << c.

5.10. Две релятивистские частицы движутся в лабораторной системе отсчета со скоростями ʋ₁ = 0,6c и ʋ₂ = 0,9c вдоль одной прямой. Определить их относительную скорость u₂₁ в двух случаях: 1) частицы движутся в одном направлении; 2) частицы движутся в противоположных направлениях.

5.11. В лабораторной системе отсчета удаляются друг от друга две частицы с одинаковыми по модулю скоростями. Их относительная скорость u u в той же системе отсчета равна 0,5c. Определить скорости частиц.

5.12. Ион, вылетев из ускорителя, испустил фотон в направлении своего движения. Определить скорость фотона относительно ускорителя, если скорость ʋ иона относительно ускорителя равна 0,8c.

5.13. Ускоритель сообщил радиоактивному ядру скорость ʋ₁ = 0,4c. В момент вылета из ускорителя ядро выбросило в направлении своего движения β-частицу со скоростью ʋ₂ = 0,75c относительно ускорителя. Найти скорость u₂₁ частицы относительно ядра.

5.14. Два ускорителя выбрасывают навстречу друг другу частицы со скоростями |ʋ| = 0,9c. Определить относительную скорость u₂₁ сближения частиц в системе отсчета, движущейся вместе с одной из частиц.

Релятивистская масса u релятивистский импульс

5.15. Частица движется со скоростью ʋ = 0,5c. Во сколько раз релятивистская масса частицы больше массы покоя?

5.16. С какой скоростью ʋ движется частица, если ее релятивистская масса в три раза больше массы покоя?

5.17. Отношение заряда движущегося электрона к его массе, определенное из опыта, равно 0,88·10¹¹ Кл/кг. Определить релятивистскую массу m электрона и его скорость ʋ.

5.18. На сколько процентов релятивистская масса частицы больше массы покоя при скорости ʋ = 3,0·10⁷ м/с?

5.19. Показать, что выражение релятивистского импульса переходит в соответствующее выражение импульса в классичекой механике при ʋ << c.

5.20. Электрон движется со скоростью ʋ = 0,6c. Определить релятивистский импульс p электрона.

5.21. Импульс p релятивистской частицы равен m₀c (m₀ – масса покоя). Определить скорость ʋ частицы (в долях скорости света).

5.22. В лабораторной системе отсчета одна из двух одинаковых частиц покоится, другая движется со скоростью ʋ = 0,8c по направлению к покоящейся частице. Определить: 1) релятивистскую массу движущейся частицы в лабораторной системе отсчета; 2) скорость частиц в системе отсчета, связанной с центром инерции системы; 3) релятивистскую массу частиц в системе отсчета, связанной с центром инерции.

5.23. В лабораторной системе отсчета находятся две частицы. Одна частица с массой покоя m₀ движется со скоростью ʋ = 0,6c, другая с массой покоя 2m₀ покоится. Определить скорость ʋ_c центра масс системы частиц.

Взаимосвязь массы u энергии

5.24. Полная энергия тела возросла на ΔE = 1 Дж. На сколько при этом изменится масса тела?

5.25. Определить, на сколько должна увеличиться полная энергия тела, чтобы его релятивистская масса возросла на Δm = 1 г.

5.26. Вычислить энергию покоя: 1) электрона; 2) протона; 3) α частицы. Ответ выразить в джоулях и мегаэлектрон-вольтах.

5.27. Известно, что объем воды в океане равен 1,37·10⁹ км³. Определить, на сколько возрастет масса воды в океане, если температура воды повысится на Δt = 1 ºC. Плотность ρ воды в океане принять равной 1,03·10³ кг/м³.

5.28. Солнечная постоянная C (плотность потока энергии электромагнитного излучения Солнца на расстоянии, равном среднему расстоянию от Земли до Солнца) равна 1,4 кВт/м². l. Определить массу, которую теряет Солнце в течение одного года. 2. На сколько изменится масса воды в океане за один год, если предположить, что поглощается 50% падающей на поверхность океана энергии излучения? При расчетах принять площадь S поверхности океана равной 3,6·10⁸ км².

Кинетическая энергия релятивистской частицы

5.29. Кинетическая энергия T электрона равна 10 МэВ. Во сколько раз его релятивистская масса больше массы покоя? Сделать такой же подсчет для протона.

5.30. Во сколько раз релятивистская масса протона больше релятивистской массы электрона, если обе частицы имеют одинаковую кинетическую энергию T = 1 ГэВ?

5.31. Электрон летит со скоростью ʋ = 0,8с. Определить кинетическую энергию T электрона (в мегаэлектрон-вольтах).

5.32. При какой скорости ʋ кинетическая энергия любой частицы вещества равна ее энергии покоя?

5.33. Определить скорость ʋ электрона, если его кинетическая энергия равна: l) T = 4 МэВ; 2) T = 1 кэВ.

5.34. Найти скорость ʋ протона, если его кинетическая энергия равна: l) T = 1 МэВ; 2) T = 2 ГэВ.

5.35. Показать, что релятивистское выражение кинетической энергии T = (m – m₀)c² при ʋ<<c переходит в соответствующее выражение классической механики.

5.36. Какая относительная ошибка будет допущена при вычислении кинетической энергии релятивистской частицы, если вместо релятивистского выражения T = (m – m₀)c² воспользоваться классическим T = m₀ʋ²/2? Вычисления выполнить для двух случаев: 1) ʋ = 0,2c; 2) ʋ = 0,8c.

5.37. Две релятивистские частицы движутся навстречу друг другу с одинаковыми (в лабораторной системе отсчета) кинетическими энергиями, равными их энергии покоя. Определить: 1) скорости частиц в лабораторной системе отсчета; 2) относительную скорость сближения частиц (в единицах c); 3) кинетическую энергию (в единицах m₀c²) одной из частиц в системе отсчета, связанной с другой частицей.

Связь энергии релятивистской частицы с ее импульсом

5.38. Показать, что выражение релятивистского импульса через кинетическую энергию p² = (l/c)²(2E₀ + T)T при ʋ<<c переходит в соответствующее выражение классической механики.

5.39. Определить импульс p частицы (в единицах m₀c), если ее кинетическая энергия равна энергии покоя.

5.40. Определить кинетическую энергию T релятивистской частицы (в единицах m₀c²), если ее импульс p = m₀c.

5.41. Кинетическая энергия релятивистской частицы равна ее энергии покоя. Во сколько раз возрастет импульс частицы, если ее кинетическая энергия увеличится в n = 4 раза?

5.42. Импульс p релятивистской частицы равен m₀c. Под действием внешней силы импульс частицы увеличился в два раза. Во сколько раз возрастет при этом энергия частицы: 1) кинетическая? 2) полная?

5.43. При неупругом столкновении частицы, обладающей импульсом p = m₀c, и такой же покоящейся частицы образуется составная частица. Определить: l) скорость ʋ частицы в единицах c) до столкновения; 2) релятивистскую массу составной частицы (в единицах m₀); 3) скорость составной частицы; 4) массу покоя составной частицы (в единицах m₀); 5) кинетическую энергию частицы до столкновения и кинетическую энергию составной частицы (в единицах m₀c²).

5.44. Частица с кинетической энергией T = m₀c² налетает на другую такую же частицу, которая в лабораторной системе отсчета покоится. Найти суммарную кинетическую энергию Tʹ частиц в системе отсчета, связанной с центром инерции системы частиц.

Механические колебания

ФОРМУЛЫ

Гармонические колебания

ФОРМУЛЫ.

Дифференциальное уравнение гармонических колебаний:

;

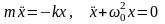здесь m – масса точки, k – коэффициент квазиупругой силы (k = mω₀²);

Уравнение механических гармонических колебаний:

,

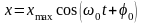здесь x – смещение от положения равновесия или значение колеблющейся величины, x_max – амплитуда колебаний, ω₀ – циклическая собственная частота, t – время, φ₀ – начальная фаза, (ω₀t + φ₀) – фаза колебаний;

Период колебаний:

,

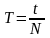здесь N – число колебаний за время t;

Частота колебаний:

;

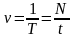Циклическая частота:

,

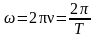Скорость и ускорение гармонических колебаний, соответственно:

,

;

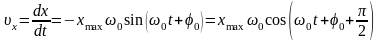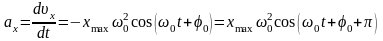Собственная частота и период колебаний математического маятника:

, ,

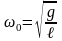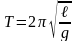здесь g – ускорение свободного падения, ℓ – длина подвеса;

Собственная частота и период колебаний физического маятника:

, ,

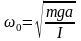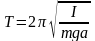здесь I – момент инерции физического маятника относительно оси колебаний, a – расстояние от центра масс маятника до оси колебаний;

Собственная частота и период колебаний пружинного маятника:

, ,

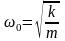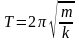здесь k – жёсткость пружины, m – масса тела, прикреплённого к пружине;

Период крутильных колебаний на упругой нити:

,

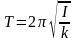здесь I – момент инерции тела относительно оси, совпадающей с упругой нитью, k – жесткость упругой нити, равная отношению упругого момента, возникающего при закручивании нити, к углу, на который нить закручивается;

Сила, возвращающая тело в положение равновесия в пружинном маятнике:

F_возвр = kx,

здесь k = mω₀²;

Кинетическая энергия, потенциальная энергия, полная энергия пружинного маятника, соответственно:

, , ;

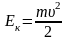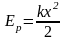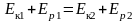Амплитуда A результирующего колебания, полученного при сложении двух колебаний с одинаковыми частотами, происходящих по одной прямой, определяется по формуле:

;

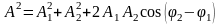здесь A₁, A₂ – амплитуды составляющих колебаний, φ₁, φ ₂ – их начальные фазы;

Начальная фаза φ результирующего колебания может быть найдена из формулы

;

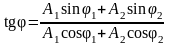Частота биений, возникающих при сложении двух колебаний, происходящих по одной прямой с различными, но близкими по значению частотами ν₁, ν₂:

ν = ν₁ – ν₂;

Уравнение траектории точки, участвующей в двух взаимно перпендикулярных колебаниях одинаковой частоты с амплитудами A₁ и A₂ начальными фазами φ₁ и φ₂:

;

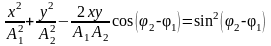Если начальные фазы φ₁ и φ₂ составляющих колебаний одинаковы, то уравнение траектории принимает вид:

,

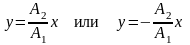т. е. точка движется по прямой;

В том случае, если разность фаз Δφ = φ ₂ – φ₁ = π/2, принимает вид

,

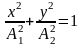т. е. точка движется по эллипсу;

Дифференциальное уравнение затухающих колебаний:

,

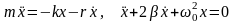здесь m – масса точки, r – коэффициент сопротивления, β – коэффициент затухания, β = r/(2m);

Уравнение механических затухающих колебаний:

,

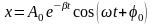здесь A₀ – начальная амплитуда, 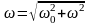– частота затухающих колебаний;

Время релаксации, логарифмический декремент затухания и добротность, соответственно:

,

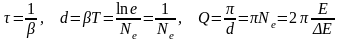здесь N_e – число колебаний, в течении которых амплитуда колебаний уменьшается в «e», E – среднее значение запасенной энергии в системе за некоторый промежуток времени, равный одному периоду колебаний, ΔE –потери энергии системе за тот же промежуток времени;

Дифференциальное уравнение вынужденных колебаний:

,

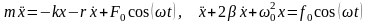здесь F₀cos(ωt) – внешняя периодическая сила, действующая на колеблющуюся материальную точку и вызывающая вынужденные колебания, F₀ – ее амплитудное значение, F₀ = F₀/m;

Амплитуда вынужденных колебаний:

,

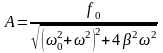Резонансная частота и резонансная амплитуда, соответственно:

.

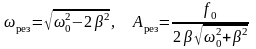Кинематика гармонических колебаний

6.1. Уравнение колебаний точки имеет вид x = Acos(ω(t + τ)), где ω = π с^–1, τ = 0,2 с. Определить период T и начальную фазу φ колебаний.

6.2. Определить период T, частоту ν и начальную фазу φ колебаний, заданных уравнением x = Asin(ω(t + τ)), где ω = 2,5π с^–1, τ = 0,4с.

6.3. Точка совершает колебания по закону x = Acos(ωt + φ), где A = 4 см. Определить начальную фазу φ, если: l) x(0) = 2 см и dx(0)/dt < 0; 2) x(0) = –2√2 см и dx(0)/dt < 0; 3) x(0) = 2 см и dx(0)/dt > 0; 4) x(0) = –2√3 см и dx(0)/dt > 0. Построить векторную диаграмму для момента t = 0.

6.4. Точка совершает колебания по закону x = Asin(ωt + φ), где A = 4 см. Определить начальную фазу φ, если: l) x(0) = 2 см и dx(0)/dt < 0; 2) x(0) = 2√3 см и dx(0)/dt > 0; 3) x(0) = –2√2 см и dx(0)/dt < 0; 4) x(0) = –2√3 см и dx(0)/dt > 0. Построить векторную диаграмму для момента t = 0.

6.5. Точка совершает колебания по закону x = Acos(ωt + φ), где A = 2 см; ω = π с^–1; φ = π/4 рад. Построить графики зависимости от времени: l) смещения x(t); 2) скорости dx/dt; 3) ускорения dx²/d²t.

6.6. Точка совершает колебания с амплитудой A = 4 см и периодом T = 2 с. Написать уравнение этих колебаний, считая, что в момент t = 0 смещение x(0) = 0, и dx(0)/dt < 0. Определить фазу (ωt + φ) для двух моментов времени: l) когда смещение x = 1 см и dx(0)/dt > 0; 2) когда скорость dx/dt = –6 см/с и x < 0.

6.7. Точка равномерно движется по окружности против часовой стрелки с периодом T = 6 с. Диаметр d окружности равен 20 см. Написать уравнение движения проекции точки на ось x, проходящую через центр окружности, если в момент времени, принятый за начальный, проекция на ось x равна нулю. Найти смещение x, скорость dx/dt и ускорение dx²/d²t проекции точки в момент t = 1 с.

6.8. Определить максимальные значения скорости (dx/dt)_max и ускорения (dx²/d²t)_max точки, совершающей гармонические колебания с амплитудой A = 3 см и циклической частотой ω = π/2 с^–1.

6.9. Точка совершает колебания по закону x = Acos(ωt), A = 3 см, ω = 2 с^–1. Определить ускорение |dx²/d²t| точки в момент времени, когда ее скорость dx/dt = 8 см/с.

6.10. Точка совершает гармонические колебания. Наибольшее смещение x_max точки равно 10 см, наибольшая скорость (dx/dt)_max = 20 см/с. Найти циклическую частоту ω колебаний и максимальное ускорение (dx²/d²t)_max точки.

6.11. Максимальная скорость (dx/dt)_max точки, совершающей гармонические колебания, равна 10 см/с, максимальное ускорение (dx²/d²t)_max = 100 см/с². Найти угловую частоту ω колебаний, их период T и амплитуду A. Написать уравнение колебаний, приняв начальную фазу равной нулю.

6.12. Точка совершает колебания по закону x = Asin(ωt). В некоторый момент времени смещение x₁ точки оказалось равным 5 см. Когда фаза колебаний увеличилась вдвое, смещение x₂ стало равным 8 см. Найти амплитуду A колебаний.

6.13. Колебания точки происходят по закону x = Acos(ωt + φ). В некоторый момент времени смещение x точки равно 5 см, ее скорость dx/dt = 20 см/с и ускорение dx²/d²t = –80 см/с². Найти амплитуду A, угловую частоту ω, период T колебаний и фазу (ωt + φ) в рассматриваемый момент времени.

Сложение колебаний

6.14. Два одинаково направленных гармонических колебания одного периода с амплитудами A₁ = 10 см и A₂ = 6 см складываются в одно колебание с амплитудой A = 14 см. Найти разность фаз Δφ складываемых колебаний.

6.15. Два гармонических колебания, направленных по одной прямой и имеющих одинаковые амплитуды и периоды, складываются в одно колебание той же амплитуды. Найти разность фаз Δφ складываемых колебаний.

6.16. Определить амплитуду A и начальную фазу φ результирующего колебания, возникающего при сложении двух колебаний одинаковых направления и периода x₁ = A₁sin(ωt), и x₂ = A₂sin(ω(t + τ)), где A₁ = A₂ =1 см; ω = π с^–1, τ = 0,5 с. Найти уравнение результирующего колебания.

6.17. Точка участвует в двух одинаково направленных колебаниях: x₁ = A₁sin(ωt), и x₂ = A₂cos(ωt), где A₁ = 1 см; A₂ = 2 см; ω = 1 с^–1. Определить амплитуду A результирующего колебания, его частоту ν и начальную фазу φ. Найти уравнение этого движения.

6.18. Складываются два гармонических колебания одного направления с одинаковыми периодами T₁ = T₂ = 1,5 с и амплитудами A₁ = A₂ = 2 см. Начальные фазы колебаний φ₁ = π/2 и φ₂ = π/3. Определить амплитуду A и начальную фазу φ результирующего колебания. Найти его уравнение и построить с соблюдением масштаба векторную диаграмму сложения амплитуд.

6.19. Складываются три гармонических колебания одного направления с одинаковыми периодами T₁ = T₂ = T₃ = 2 с и амплитудами A₁ = A₂ = A₃ = 3 см. Начальные фазы колебаний φ₁ = 0, φ₂ = π/3, φ₃ = 2π/3. Построить векторную диаграмму сложения амплитуд. Определить из чертежа амплитуду A и начальную фазу φ результирующего колебания. Найти его уравнение.

6.20. Складываются два гармонических колебания одинаковой частоты и одинакового направления: x₁ = A₁cos(ωt + φ₁) и x₂ = A₂cos(ωt + φ₂). Начертить векторную диаграмму для момента времени t = 0. Определить аналитически амплитуду A и начальную фазу φ результирующего колебания. Отложить A и φ на векторной диаграмме. Найти уравнение результирующего колебания (в тригонометрической форме через косинус). Задачу решить для двух случаев: l) A₁ = 1 см, φ₁ = π/3, A₂ = 2 см, φ₂ = 5π/6; 2) A₁ = 1 см, φ₁ = 2π/3, A₂ = 1 см, φ₂ = 7π/6.

6.21. Два камертона звучат одновременно. Частоты ν₁ и ν₂ их колебаний соответственно равны 440 и 440,5 Гц. Определить период T биений.

6.22. Складываются два взаимно перпендикулярных колебания, выражаемых уравнениями x = A₁sin(ωt), y = A₂cos(ω(t + τ)), где A₁ = 2 см, A₂ = 1 см, ω = π с^–1, τ = 0,5 с. Найти уравнение траектории и построить ее, показав направление движения точки.

6.23. Точка совершает одновременно два гармонических колебания, происходящих по взаимно перпендикулярным направлениям и выражаемых уравнениями x = A₁cos(ωt), и y = A₂cos(ω(t + τ)), A₁ = 4 см, A₂ = 8 см, ω = π с^–1, τ = 1 с. Найти уравнение траектории точки и построить график ее движения.