
Олимпиада2021_1 тур решения
.pdfМАТЕМАТИЧЕСКАЯ ОЛИМПИАДА – 2021 год
№1. (4 балла). Школьники купили в буфете конфеты: ириски и ”Белочки”, потратив на покупку одну и ту же сумму каждый. Вовочка купил и съел четверть всех ирисок и шестую часть всех ”Белочек”. Сколько школьников покупали конфеты?
Решение. Пусть m – общая стоимость всех ирисок, p – общая стоимость всех ”Белочек”, n – число школьников, S – сумма, потраченная каждым школьником.
Тогда |
|
(4mS |
+ |
6pS = 1. |
|||||
(m4 + p6 = S |
|||||||||
m + p = Sn, |
|
|
m |
+ |
p |
= n, |
|||
|
|
|
|
S |
|
S |
|||
Обозначив m/S = x и p/S = y, имеем |
|
|
|
|
|
|
|
|
|
|
(x + 2n = 12. |
||||||||
(x4 + y6 = 1 |
|
||||||||
x + y = n, |
|
|
y = n |
− x, |
|||||
Отсюда x – целое четное число не более 4. Если x = 0, то m = 0, т.е. ириски не покупались. Если x = 4, то y = 0, p = 0, ”Белочки” не покупались. Таким образом, x = 2 и n = 5 – школьников пять.
Ответ: n = 5.
№2 (6 баллов). Дана матрица |
|
−2 |
|
. |
||
|
|
A = |
1 |
1 |
||
|
|
|
2 |
−1 |
0 |
|
|
|
0 |
−1 |
5 |
||
+ A100 |
|
|
|
|
|
|
Найти det A99 |
. |
|
|
|
|
|
Решение. |
|
|
|
|
|
|
det A99 + A100 |
= det |
A99 (E + A) = det A99 ·det (E + A) = (det A)99·det (E + A) . |
|||||||||||||||||||||||||||
|
|
|
det A = |
|
1 |
−2 |
1 |
= |
|
13; |
|
det (E + A) = |
|
1 |
−1 |
1 |
= |
9. |
|
|
|
|
|||||||
|
|
|
|
|
|
2 |
1 |
0 |
|
|
− |
|
|
|
|
|
|
|
|
3 |
1 |
0 |
|
− |
|
|
|
|
|
|
|
|
|
|
0 |
−1 5 |
|
|
|
|
|
|
|
|
0 |
−1 6 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
det A |
99 |
|
|
100 |
= (−13) |
99 |
|
|
|
|
99 |
|
|
|
|
|
|
|
|||||
Ответ: 9 · 1399. |
|
|
+ A |
|
|
· (−9) = 9 · 13 . |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
→− |
|
c |
|
|
|
|
|
|
|
a |
+ |
→− + |
c |
|
№3 (4 балла). Модули трех векторов →− |
, |
b |
|
|
|
|
|
|
|
|
|
b |
|
||||||||||||||||
|
, →− равны 3, модуль вектора →− |
|
|
|
→− |
||||||||||||||||||||||||
3 |
√ |
|
|
|
|
|
|
a |
|
→− |
|
→− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
c |
|
|
|
ϕ |
|
|
|
|
|
a |
|
c |
||||||||
равен |
|
|
. Известно, что →− |
b |
и |
b |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
→− . Найти угол |
|
|
между векторами →− и |
→− . |
|||||||||||||||||||||
1

|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
c |
|
|
|
|
|
|
a |
|
|
b |
c |
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Решение. По условию |
|
|
a = −→ |
|
|
= |
−→ |
= 3 |
и |
|
−→ |
+ |
−→ + |
−→ |
|
= 3 2 |
|
||||||||||||||||||
|
−→ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. Пользуясь |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
свойством скалярного произведения,| | |
|
получим| | |
|
|
|
|
−→ |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
−→ |
+ |
−→ |
+ −→ |
= −→ + |
−→ + |
|
= 18 |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
a |
|
|
|
|
b |
|
c |
|
|
|
|
|
a |
|
b |
|
|
|
c |
|
|
. |
|
|
|
|
|
||
С другой стороны, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
a |
| |
2 |
|
b |
|
2 |
c |
|
2 |
|
|
|
a b |
|
|
b c |
|
|
a c |
|
|
. |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|→− |
|
+ →− |
|
+ |→− | |
|
|
+ 2→− |
→− + 2→− |
→− + 2→− →− |
= 18 |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− 27 |
a |
b |
|
b |
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
c |
|||
Так как →− |
→− и →− →− , то |
из последнего равенства следует, что 2→− →− = 18 |
|||||||||||||||||||||||||||||||||
a |
c |
ϕ |
= |
−9. Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
или 2 |→− | |→− | cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
cos ϕ = −0,5 |
|
|
ϕ = 120◦. |
|
|
|
|
|
|
|||||||||||||||||
Ответ: 120◦. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
№4 (4 балла). Найти f0(0), если f(x) = (3x + 2)f x2 + 2.
Решение.
f(0) = 2f(0) + 2 f(0) = −2. f0(x) = 3f(x2) + (3x + 2)f0(x2) · 2x. f0(0) = 3f(0) = −6.
Ответ: f0(0) = −6.
№5 (4 балла). Найти x, если q9 x5p9 x5√9 x5 . . . = √8 32. Решение. Перепишем уравнение следующим образом
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
5 |
|
|
5 |
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
+ |
|
|
|
+ |
|
+... = 28 . |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
9 |
81 |
729 |
|
|
|
|
|
|
|||||||||||||||
Вычислим сумму: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|||||
|
|
5 |
|
|
|
|
5 |
|
|
5 |
|
|
|
|
|
|
|
|
|
|
5 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|||||||||||||
|
|
|
|
|
+ |
|
|
|
|
+ |
|
|
|
|
+ . . . = |
|
|
|
|
|
= |
|
. |
|
|
||||||||
|
|
|
|
|
|
|
2 |
3 |
|
|
− |
1 |
|
|
|
||||||||||||||||||
|
|
9 |
9 |
|
|
|
9 |
|
|
|
|
|
|
|
1 |
|
9 |
8 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
5 |
5 |
, откуда x = 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Тогда x8 = 2 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Ответ: x = 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
n |
|
ik |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
№6 (4 балла). Вычислить lim |
Xk |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
5k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Решение. |
|
|
n→∞ |
|
=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
n |
|
ik |
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
i2 |
|
|
|
|
in |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|||||||||||||
|
|
n→∞ k=0 |
5k = n→∞ |
|
5 |
52 + + |
5n |
||||||||||||||||||||||||||
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
lim |
|
|
|
|
|
|
lim |
|
|
|
1 + |
|
|
|
|
|
|
|
|
. . . |
|
|
. |
||||||||
2

Данный предел равен сумме бесконечно убывающей геометрической прогрессии,
|
q = i |
|
i |
|
< 1 |
|
|
|
|
|
|
|
|
||||||
знаменатель которой |
|
n |
|
|
k( |
|
|
|
|
|
). Таким образом, |
|
|
||||||
|
5 |
5 |
|
|
|
|
|||||||||||||
|
|
Xk |
|
i |
|
|
|
|
|
1 |
|
|
|
|
5(5 + i) |
|
5 |
|
|
lim |
|
|
|
k |
= |
|
− |
|
i = |
− |
= |
|
(5 + i). |
||||||
n→∞ |
=0 |
5 |
|
|
|
|
1 |
|
|
5 |
|
|
(5 i)(5 + i) |
26 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: 265 (5 + i).
№7 (8 баллов). Найти значения параметров a > 0 и b, при которых
|
|
|
|
|
x→∞ p |
|
|
|
|
|
|
|
|
− |
|
|
− |
|
|
|
|
|
|
|
||||||||
|
|
|
|
x2 + 4x |
− |
13 |
ax |
b |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
= 0. |
|
|
|
||||||||||||||
Решение. |
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
x→∞ |
|
|
+ 4 − 13 − |
ax |
− |
= |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
lim |
|
x2 |
x |
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|||||||
|
→∞ |
|
|
|
|
|
|
|
|
+ 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
√x2 + 4x − 13 − (ax + b) |
|
|
|
√x2 + 4x − 13 + (ax + b) |
||||||||||||||||||||||||
= xlim |
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
= |
|
||||||||||||||||
|
|
|
|
x2 |
|
x |
− |
13 + (ax + b) |
|
|
|
|||||||||||||||||||||
|
x2 + 4x − 13 − (ax + b)2 |
|
|
x2(1 − a2) + x(4 − 2ab) − (13 + b2) |
|
|||||||||||||||||||||||||||
= lim |
= lim |
. |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
x→∞ |
√x2 + 4x − 13 + ax + b |
x→∞ |
|
|
|
|
|
|
|
√x2 + 4x − 13 + ax + b |
||||||||||||||||||||||
Предел равен нулю, если
1 − a2 = 0,
4 − 2ab = 0.
Отсюда a = 1, b = 2.
Ответ: a = 1, b = 2.
№8 (4 балла). Решить уравнение e8z + 32e4z + 256 = 0, где z = x + iy. Решение. Пусть y = e4z, тогда
y2 + 32y + 256 = 0 y1,2 = −16.
e4z = −16 4z = ln 16 + i(π + 2πk), k = 0, ±1, ±2 . . .
|
|
|
|
|
|
|
||
|
|
|
|
π |
πk |
, k = 0, ±1, ±2 . . . |
||
z = ln 2 + i |
|
4 |
+ |
2 |
|
|||
π |
πk |
|
|
|
|
|
|
|
Ответ: z = ln 2 + i 4 +π |
2 , |
k = 0, ±1, ±2 . . . |
||||||
№9 (8 баллов). Сравнить Z0 |
|
2 |
|
|
|
π |
|
|
|
esin |
xdx и |
3 |
. |
|
|||
|
2 |
|
||||||
3

Решение. При x > 0 ex > 1 + x. Следовательно, |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
esin2 x > 1 + sin2 x. |
|
|
|
|
|
|
|||||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx = |
|
π |
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
π |
2 |
|
|
|
|||||
Z esin |
xdx > Z |
|
1 + sin2 x dx = Z 1 + 1 − |
|
|
|
||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos 2x |
||||||
0 |
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
||||
|
π |
|
|
|
|
|
|
|
|
dx = |
2 |
|
|
|
|
π |
|
|
|
|
|
|||
= |
Z |
2 − |
|
|
2 |
|
|
|
|
|
= |
2 . |
||||||||||||
|
|
|
− 4 sin 2x 0 |
|||||||||||||||||||||
|
0 |
|
3 |
cos 2x |
3 |
1 |
|
|
|
3π |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
№10 (10 баллов). Доказать, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
a |
|
|
|
|
a |
f(x) dx, |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
Z |
1 + ex dx = Z |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
f(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
−a |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
если известно, что функция f(x) – четная и непрерывная на отрезке [−a, a].
Решение.
|
|
|
a |
|
|
|
|
0 |
|
|
|
|
|
a |
|
|
|
|
|
|||||||
|
|
|
Z |
1 + ex dx = Z |
1 + ex dx + Z |
|
1 + ex dx = |
|
|
|||||||||||||||||
|
|
|
|
|
f(x) |
|
|
|
|
|
f(x) |
|
|
|
|
|
f(x) |
|
|
|
||||||
|
|
|
−a |
|
|
|
|
|
−a |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|||
|
|
0 |
|
|
|
|
|
a |
|
|
|
0 |
|
|
|
|
|
|
a |
|
|
|
||||
|
|
|
f( t) |
|
|
f(x) |
|
|
|
|
f(t)et |
|
|
f(x) |
||||||||||||
= − Za |
|
− |
dt + Z0 |
|
|
|
dx = |
− Za |
|
|
dt + Z0 |
|
dx = |
|||||||||||||
|
1 + e−t |
1 + ex |
1 + et |
1 + ex |
||||||||||||||||||||||
a |
f x ex |
|
a |
|
f(x) |
|
a |
f(x)(1 + ex) |
|
|
a |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
= Z0 |
( ) |
dx + Z0 |
|
dx = Z0 |
|
|
|
|
dx = Z0 |
f(x) dx. |
||||||||||||||||
1 + ex |
1 + ex |
|
|
1 + ex |
||||||||||||||||||||||
№11 (4 балла). Вычислить двойной интеграл I = |
RR |
|
|
|
|
|
||||||||||||||||||||
|
x2dxdy, где |
|
|
|||||||||||||||||||||||
G
G= (x, y) : x2 ≤ y(4 − y) .
Решение. G : x2 + (y − 2)2 ≤ 4.
4

 y
y
2
1
0 |
1 |
x |
Введем полярные координаты x = r cos ϕ, y = 2 + r sin ϕ, где 0 ≤ r ≤ 2, 0 ≤ ϕ ≤ 2π. Тогда
|
I = ZZ |
|
|
|
|
|
2π |
|
|
2 |
|
|
|
|
|
|
|
|
r2 cos2 ϕ · rdrdϕ = Z |
cos2 ϕdϕ · Z |
r3dr = |
|
|||||||||||||
|
|
G0 |
|
|
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|
2π |
|
|
|
2 |
|
|
|
|
|
2π |
|
|
4 |
2 |
|
||
= Z 1 + |
2 |
|
dϕ · Z |
r3dr = |
|
|
|
|
|
|
= 4π. |
||||||
|
2ϕ + 4 sin 2ϕ 0 |
· |
4 |
0 |
|||||||||||||
0 |
|
cos 2ϕ |
|
|
1 |
1 |
|
|
r |
|
|
|
|||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: 4π.
№12 (6 баллов). Найти длину дуги кривой x2 + y2 = 2ax + 2by, расположенной в первой четверти (a > 0, b > 0).
Решение. Приведем уравнение x2 + y2 = 2ax + 2by к каноническому виду
(x − a)2 + (y − b)2 = a2 + b2.
 y
y
b








0 |
a |
x |
5

Центр окружности (a, b), точки пересечения окружности с осями координат (0, 2b)
и (2a, 0) лежат на одной прямой. Таким образом, половина окружности лежит в |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π√ |
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2+b2 |
|
|
|
|
|||||
первой четверти. Следовательно, искомая длина равна |
a |
2 |
2 |
. |
|||||||||||||||||||||||||
|
2 |
|
|
= π |
|
+ b |
|||||||||||||||||||||||
Ответ: π√ |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
a2 + b2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
№13 (8 баллов). Решить дифференциальное уравнение y0(t) = |
1 |
(y(t) + y(−t)). |
|||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||
|
2 |
||||||||||||||||||||||||||||
Решение. |
|
|
|
|
|
y0 |
t |
1 |
|
|
y t |
|
y |
t |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
( ) = |
|
|
( |
( |
) + |
|
|
(− )) |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
y00 t |
1 |
y0 |
t |
y0 |
|
t |
1 |
y t |
|
y |
t |
y t |
y |
t |
|
|
|
|
|||||||||||
2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
( ) = |
( |
( ) − |
|
(− )) = |
4 ( ( ) + |
|
|
(− ) − |
( ) − |
|
(− )) = 0 |
|
|
||||||||||||||||
y00(t) = 0 y(t) = C1t + C2.
Так как y0(t) = C1 = 12 (C1t + C2 − C1t + C2) = C2, то y(t) = C1(t + 1). Ответ: y(t) = C1(t + 1).
№14 (4 балла). Вероятность того, что студент сдаст экзамен по математике, равна 0,4. Вероятность того, что студент сдаст экзамен, по крайней мере, по математике или физике, равна 0,6. Вероятность того, что студент сдаст математику и физику, равна 0,1. Найти вероятность того, что студент сдаст физику.
Решение. Обозначим через A событие "студент сдаст математику", через B "студент сдаст физику". Тогда P (A) = 0,4. Требуется найти P (B). По условию P (A + B) = 0,6, P (A · B) = 0,1. По теореме сложения совместных событий
P (A + B) = P (A) + P (B) − P (A · B),
0,6 = 0,4 + P (B) − 0,1.
Следовательно, P (B) = 0,3.
Ответ: 0,3.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 |
1 |
|
|
|
|
|
№15 (6 баллов). Пусть Φ(x) – сумма ряда Фурье функции f(x) |
= |
x |
|
−1 |
|
на |
||||||||||||||||||||
интервале (−2, 2), f(x + 4) = f(x). Построить график Φ(x). |
|
|
|
|
|
|
− |
|
|
|
||||||||||||||||
Решение. Вычислим |
|
x→1−0 |
x |
|
|
|
x→1−0 |
− |
− |
|
− |
|
|
|
− |
|
||||||||||
x→1+0 |
x |
|
1 |
|
x→1+0 |
|
|
1 |
|
|
|
|
|
|||||||||||||
lim |
|
x3 |
− 1 |
|
= lim (x2 |
+ x + 1) = 3, |
lim |
|
x3 |
− 1 |
|
= |
lim ( |
x2 |
|
x |
|
|
1) = |
|
|
3. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
− |
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Следовательно, x0 = 1 (−2, 2) единственная точка разрыва первого рода. В остальных точках интервала (−2, 2) функция f(x) непрерывна и дифференцируема. Следовательно, Φ(x) = f(x), x (−2, 2) \ {1}. По теореме Дирихле находим
6
значение Φ(x) в точках разрыва. |
|
|
|
|
Φ(1) = |
f(1 − 0) + f(1 + 0) |
= |
−3 + 3 |
= 0, |
2 |
|
2 |
|
|
Φ(−2) = Φ(2) = f(−2 + 0) + f(2 − 0). 2
Вычислим f(−2 + 0) и f(2 − 0):
x→−2+0 |
x |
|
1 |
|
− |
|
x→2−0 |
x |
|
1 |
|
||||
lim |
|
x3 |
− 1 |
|
= |
|
3, |
lim |
|
x3 |
− 1 |
|
= 7. |
||
|
|
|
|
|
|
|
|
|
|||||||
|
|
− |
|
|
|
|
|
|
− |
|
|
||||
Таким образом,
Φ(−2) = Φ(2) = −3 + 7 = 2. 2
Построим график Φ(x):
y
7
3
1
−6 |
−3 −2 |
0 |
1 2 |
5 6 |
x |
|
−3 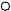
7
