Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Башкирский Государственный Аграрный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

книги2 / 337

.pdf

Скачиваний:

Добавлен:

25.02.2024

Размер:

3.47 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 65 6 > Следующая >>>

Физико-математические науки

СПЕКТРАЛЬНАЯ ЗАДАЧА МОРАВЕЦ ДЛЯ ОБОБЩЕННОГО УРАВНЕНИЯ ТРИКОМИ

Акимов Андрей Анатольевич

кандидат физико-математических наук доцент кафедры математического анализа

Агафонова Алена Александровна

институт педагогики и психологии

Стерлитамакский филиал Башкирского государственного университета

Аннотация. Рассмотрена задача Моравец, ко-	Рассмотрим уравнение
торая является математической моделью сверх-
звуковых течений. Найдены собственные значения	(1)
и построена соответствующая система собствен-	(1)
ных функций спектральной задачи для обобщенно-	где	в области D, ограниченной
го оператора Трикоми с однородными смешанными
граничными условиями.	кривой	лежащей
Ключевые слова: задача Моравец, уравнение
Трикоми, уравнения смешанного типа, спектраль-	вполуплоскостиy>0сконцамивточкахK(-1,0)иB
ная задача, собственные функции.	(1, 0) отрезком AK оси OX где A = (0, 0), и характери-
	(1, 0) отрезком AK оси OX где A = (0, 0), и характери-
	стиками g1 и g2	уравнения (1) при y < 0:

	Для уравнения (1) в области D изучим спек-	(6)
	тральную задачу (задача Mλ), соответствующую	(6)
	задаче типа Моравец.
	ЗадачаMλ.Найтизначенияλисоответствующие	где
	им функции u (x, y), удовлетворяющие условиям:	Частные решения задачи Mλ построим методом
		Частные решения задачи Mλ построим методом
	(2)	разделения переменных соответственно в обла-
	(3)	стяхэллиптичностиигиперболичности.Вобласти
	(3)	D перейдем к новым переменным
	(4)	D перейдем к новым переменным

Тогда уравнение (1) примет вид

(5)

Разделяя	здесь	переменные	(8)
u(r,j ) = R(r) (j ),	получим	два обыкновен-

ных дифференциальных уравнения

	(9)
(7)	ВЫСШАЯ ШКОЛА • №23 / 2023	(10)
	ВЫСШАЯ ШКОЛА • №23 / 2023	41

Физико-математические науки

Построим общее решение краевой задачи (9) и (10). Для этого в (9) введем новую переменную t = cos2(j /2). Тогда уравнение примет вид

(11)

Уравнение (11) является известным гипергеометрическим уравнением, поэтому его общее решение определяется по формуле [1]

	1		j			2j	1	b	1		1		3		2j
				+			2
(j ) = C1+ F b + g,b g,		+ b;cos2		+ C2	cos				F 2	+ g,		g,		b;cos		,	(12)
	2					2					2		2		2
			2

где C1+ ,C2+ − произвольные постоянные. Подставляя (12) во второе краевое условие (10), получим C1+ = 0. . Известно, что решением уравнения (7) является функция Бесселя

R(r) = r b Jg (		r), g =	m2 + b 2	.
	l				(13)

Удовлетворяя (13) граничным условиям (8), имеем

(14)

Таким образом, частные решения уравнения (1) области D удовлетворяющие краевым условиям (4) и (6), имеют вид

2 b

u = C + r b J

()l r 2

+ g,

cos

В уравнении (1) в области D- сделаем замену переменных

x + x2

m+2

( y) 2

m+2

= x2

m + 2

( y) 2 , 0 < s < 1,

q =

, q > 1.

m + 2

2 x2

( y)

m+2

m + 2

Тогда в координатах (s ,q) уравнение (1) примет вид

Разделяя в последнем уравнении переменные u(s ,q) = Q(q)P(s ),

получим

Решением уравнения (16), удовлетворяющим условиям (17), является функция

Уравнение (18) является гипергеометрическим уравнением с аргументом q > 1. Переходя к аргументу 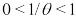построим его общее решение

(b +g)		1			1		(b g)			1			1
Q(q) = C q	F b + g,		+ g,1	+ 2g;		+ C	2	q	F b g,		g,1	2g;		.

1		2			q					2			q

(15)

(16)

(17)

(18)

(19)

При C2 = 0 функция Q(q) удовлетворяетграничнымусловиям(19).Тогдарешениеуравнения(18),

42 ВЫСШАЯ ШКОЛА • №23 / 2023

удовлетворяющее условиям (19) имеет вид

Физико-математические науки

Q(q) = C F b + g,

+ g,1 + 2g;

,C = C .

Таким образом, частные решения уравнения (1) в области D , удовлетворяющие раничному усло-

вию (5), определяются равенством

u = C s Jg ( l s )q (

)F b + g,

+ g,1

+ 2g;

(20)

Длянахождениясобственныхзначенийисобственныхфункцийспектральной Ml

,построеннуюси-

стему функций (15) и (20), удовлетворим условиям склеивания (2). Для этого вычислим:

Приравниваяфункции

Получим систему для нахождения C+, C-, γ.

После преобразований данная система сводится к уравнению

Отсюда найдем g , затем постоянные C+ ,C и

g = gn = 1	b	+ n,n = 1,2,...,		C + = C		(1 b + g)(1 + 2g)	.

4	2					(3/2 b ) (1/2+ g
Собственные значения спектральной задачи Ml					являются корнями уравнения (14). Тогда, обозна-
чая через a mgn − m-ый корень уравнения (14), находим собственные значения задачи Ml :
			g	2
			n		,m = 1,2....
		l n,m = a m

ВЫСШАЯ ШКОЛА • №23 / 2023 43

Физико-математические науки

Тогда справедлива следующая

Теорема 1. Собственные значения задачи (2)-(6) находятся как корни уравнения (14), а соответствующая система собственных функций определяется по формулам

Аналогично работе [2] можно доказать следующее утверждение.

Теорема 2.Система собственных функций (*) задачи Ml полна в пространствах L2(D+ ) и L2(D ), но не полна L2(D). ■

Список литературы

1.Акимов А.А. О единственности решения задачи типа Неймана для уравнения Чаплыгина // Вестник Московского областного государственного университета. 2013. № 4. С. 38.

2.Вильдяева А.А., Акимов А.А. Построение дифференциального уравнения с заданной симметрией // Сборник научных трудов Sworld. 2014. Т.29. №4. С.57-59.

3.Казакова Е.А., Акимов А.А. Построение общего решения обыкновенного дифференциального уравнения ме - тодами группового анализа // Сборник научных трудов Sworld. 2014. Т.29. №4. С.55-57.

4.Акимов А. А. Задача Моравец для обобщенного уравнения Трикоми // Сибирские электронные математиче - ские известия. 2006. Т. 3. С. 71.

5.Акимов А. А. Об одной теореме единственности решения задачи Моравец // Альманах современной науки и образования. 2010. № 12. С. 67-69.

6.Сабитов К.Б., Карамова А.А. Решение одной газодинамической задачи для уравнения смешанного типа с не- гладкой линией вырождения // Дифференциальныеуравнения. 2002. Т. 37. № 1. С. 111.

44 ВЫСШАЯ ШКОЛА • №23 / 2023

Физико-математические науки

СОВЕРШЕНСТВОВАНИЕ БИМОМЕНТНОЙ ТЕОРИИ ИЗГИБОВ И КОЛЕБАНИЙ ТОЛСТОЙ ПЛАСТИНЫ

Усаров Махаматали Корабоевич

доктор физико-математических наук, профессор Институт механики и сейсмостойкости сооружений им. М.Т. Уразбаева АН РУз,

Ташкент, Узбекистан.

Аннотация.	Статья	посвящена	Приведенныйобзоризвестныхработпоказыва-
совершенствованию бимоментной теории изгиба и			ет, что теории и методы расчета развиты в недо-
колебаний толстых ортотропных пластинв рам -			статочно полной мере. Вместе с тем, недостаточно
ках трехмерной динамической теории упругости.			полно проанализированы процессы, происходя-
Представлены уравнения движения пластины и			щие в толстых пластинах, изготовленных из мате-
граничные условия для определения обобщенных			риалов, обладающих анизотропными свойствами.
перемещений ортотропных пластин относительно			Наряду с этим, в недостаточной степени разрабо-
сил, моментов, бимоментов. Построены уравнения			таны и развиты аналитические и численные мето-
движениядляопределенияперемещенийлицевыхпо-			ды решений статических и динамических задач с
верхностейпластины.Рассмотреныпримерырасче-			учетом нелинейных законов распределения пере-
та изгиба и колебаний изотропных и ортотропных			мещений и напряжений, которые являются при-
пластин. Полученные численные результаты пока-			чиной появления не только сил и моментов, но и
зали эффект учета бимоментов при оценке напря-			бимоментов в поперечных сечениях пластины. В
женно-деформированного состояния толстых пла-			теориипластиниоболочекдонастоящеговремени
стин.			непостроеныточныевыражениядляопределения
Ключевые слова: Толстая ортотропная пла-			сил и моментов и в недостаточной мере приложе-
стина, закон Гука, трехмерная теория упругости,			ныееновыедостиженияврасчетахнасейсмостой-
уравнения движения, граничные условия, бимомент-			кость зданий и сооружений.
ная теория, бесконечный ряд, внешняя нагрузка.			Данная статья посвящена разработке теории и
Введение. Разработка методики расчета на			методов расчета толстых элементов конструкций
			на основе бимоментной теории пластин. При по-
прочность пластин занимает особое место в об-			строении теории учитываются все силовые фак-
ласти исследования элементов конструкции и			торы пластины, включая бимоменты, а также все
инженерных сооружений. С обзором работ по ме-			компоненты тензоров напряжения и деформации
тодике построения уточненной теории пластин и			σij, εij, (i, j = 1,3). Компоненты вектора перемеще-
оболочек можно ознакомиться в монографии С.А.			ния представляются в виде функции трех про-
Амбарцумяна [1]. При построении общей теории			странственных координат и времени u1(x1,x2	,z,t),
пластин в рамках трехмерной теории упругости			u2(x1,x2,z,t), u3(x1,x2,z,t). Отметим, что бимоментная
исследователи используют различные методы [2-			теория пластин, разработанная в [7-9], описывает-
6], например, метод гипотез, метод разложения			ся двумя несвязанными системами дифференци-
перемещений в ряд или метод асимптотического			альных уравнений движения, которые описывают
решения и т.д.			симметричную и асимметричную задачи, каждая
В общем пространственном случае деформи-			из которых формулируется на основе девяти дву-
рования толстой пластины по её толщине необхо-			мерныхуравненийссоответствующимикраевыми
димо учитывать все компоненты тензора напря-			условиями. Определяющие соотношения и уравне-
жения и деформации σij	, εij, (i, j = 1,3). В отличие от		ния равновесия бимоментной теории пластин раз-
классического подхода, для описания поля про-			работанысиспользованиемзаконаГука(1)иурав-
странственного деформирования пластины учет			нения теория упругости (2) и приведены в работах
растягивающих и перерезывающих сил, изгибаю-			[7-9].
щих и крутящих моментов недостаточен, допол-			В данной статье приводится методика совер-
нительно необходимо учитывать и бимоменты. В			шенствования разработанной бимоментной те-
данной статье кратко приведены определяющие			ории толстых пластин, которая осуществляется
соотношения, уравнения движения, граничные ус-			построением новых уравнений движения относи-
ловия бимоментной теории пластин, разработан-			тельно шести перемещений двух лицевых поверх-
ной в [7-9].			ВЫСШАЯ ШКОЛА • №23 / 2023	45
			ностей пластины и соответствующих граничных

Физико-математические науки

условий. Отметим, что эти новые уравнения со- ставляют совместные замкнутые системы с су- ществующими уравнениями относительно бимо-

менттов, построенными в работах [7-9]. Постановка задачи. Рассматривается орто-

тропная толстая пластина постоянной толщины H =2h и с размерами a, b в плане. Вводятся обозна-

чения: E1, E2, E3 – модули упругости; G12, G13, G23- мо- дули сдвига; v12, v13, v23- коэффициенты Пуассона и

r – плотность материала пластины.

Для описания движения пластины вводится декартовая система координат с переменными x1, x2 и z. Ось oz направлена вниз. Начало координат расположено в срединной поверхности пластины. По двум лицевым поверхностям пластины z = -h и z = +h приложены распределенные поверхностные, нормальные и касательные нагрузки. Нормальные нагрузкиq3(+),q3(-) приложены в направлении осиoz. Касательные нагрузки qk(+), qk(-), (k = 1,2) – в направ-

лении ox1, ox2.

Компоненты вектора перемещения определя- ютсяввидефункцийтрехпространственныхкоор-

динат и времени u1(x1,x2,z,t), u2(x1,x2,z,t), u3(x1,x2,z,t).

Компоненты тензора деформации определяют- ся следующими соотношениями Коши. Пластина рассматривается как трехмерное тело, материал которой подчиняется обобщенному закону Гука

σ11	= E11ε11	+ E12ε12	+ E13ε13,
σ22	= E21ε11	+ E22ε32	+ E23ε33, σ33= E31ε11+ E32ε22	+ E33ε33,
σ12	= 2G12ε12, σ13 = 2G13ε13, σ23 = 2G23ε23,			(1)
где E11, E12, ... E33–упругиеконстанты,определяе-
мые через коэффициенты Пуассона и модули упру-
гости [5,6].
Пластинарассматриваетсякактрехмерноетело

и в качестве уравнения движения пластины при- мем трехмерные уравнения теории упругости [1]:

	s k1		s k		s k3	&&		(k = 1,3)	(2)
	x1	+ x2			z	&&			(2)
	x1	+ x2		+	z	= r uk	,
Граничные условия на нижней и верхней по-
верхностях								следующий вид:
									(3)

Вводятся грузовые члены для уравнения дви-

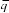
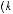
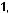
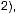
жения симметричной задачи 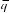, кото- рые определяются по формулам:

(4)

Аналогично, вводятся грузовые члены для

Перемещения точек на лицевых поверхностях пластины z = -h иz = +h обозначим через ui(-), ui(+), (i = 1,3)анапряженияналицевыхповерхностяхz = -h и

z= +h через σ11(-), σ12(-), σ22(-) и σ11(+), σ12(+), σ22(+).

Симметричная задача бимоментной теории

пластин состоит из двух уравнений относительно продольных, тангенциальных усилий и четырех дополнительно построенных уравнений бимомен- тов относительно девяти неизвестных кинемати- ческих функций, определяемых выражениями:

(6)

Здесь необходимо отметить, что построено шесть уравнений, в которых содержатся девять неизвестных функций, не хватает ещё трех урав- нений.

Теперь рассмотрим асимметричную задачу би- моментной теории. Асимметричная задача бимо- ментной теории пластин также состоит из шести уравнений относительно изгибающих, крутящих моментов, перерезывающих сил и бимоментов от- носительно девяти неизвестных кинематических функций, определяемых соотношениями:

(7)

Построенные уравнения асимметричной зада- чисоставляютсовместнуюсистемуизшестиурав- ненийотносительнодевятинеизвестныхфункций

~		~		,	~	,	~		,	~	,	~	,	~	~	,	~
y	1	, y	2	,	u	,	u	2	,	b	,	b	,	r,	g	,	W .
	1		2		1			2		1		1

Как в симметричной, так и в асимметричной задачах не хватает по три уравнения. Для постро- ения этих шести не хватающих уравнений исполь- зованытрехмерныеуравнениятеорииупругостии методразложениякомпонентыперемещениявряд Маклорена.

Запишем уравнения теории упругости на лице- вых поверхностях толстой пластины. Уравнения движения теории упругости на лицевой поверхно- сти пластин z = +h запишутся в виде

(8)

уравнения асимметричной задачи

,(k = 1,2),

определяются в виде:

qk+ + qk

, (k = 1,2),

q3+ q3

(5)

Уравнения теории упругости на лицевой по-

qk =

верхности z = -h имеют следующий вид:

46 ВЫСШАЯ ШКОЛА • №23 / 2023

Физико-математические науки

(9)													(16)
(9)													(16)

Сложив почленно уравнения (8) и (9), получим

Сложив соответственно первые и вторые урав-

уравнения движения в виде:

нения систем (8) и (9), получим следующие два

уравнения:

(17)

(10)

Следует отметить, что уравнения движения

(10), (12) и (15), (17) служат для определения пере-

мещений

лицевых

поверхностей пластины

, W

и u~

, u~ , W .

где бимоменты

определяются по

В уравнениях

и (17) интенсивности бимо-

формулам

ментов

определяются через полу-

разности и полусуммы производных по координа-

те

z от касательных и нормального напряжений

, имеющих следующий вид:

s~3*k

	1		s
	1	k3
=
=	2		z
	2		z	z		h
				z	=+	h
					=+

s k3z


	= G3k

z= h

	~				~
	Rk			a
			+			(k = 1,3

		2		xk
H

(11)	(18)
(11)
Вычитая третье уравнение системы (9) из урав-
Вычитая третье уравнение системы (9) из урав-
нения (8), получим уравнение:
нения (8), получим уравнение:

q1		q2			s	3*	&&
x	+	x	2	+	H = r W .
1			2				(12)
							(12)

В уравнениях (10) и (12) интенсивности бимо-

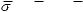
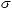
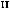
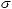
ментов определяются через полу- разности и полусуммы производных по координа- теzоткасательныхинормальногонапряженийσ13, σ23 и σ33 имеющих следующий вид:

1,3 ,

(13)

= E

+ E

(14)

(19)

Чтобы

определить

неизвестные

функции

Rk , a 1,

a 1, R, a

выражений (13), (14) и неизвест -

ные функций

выражений

R1,

R2,

a 1,

(18),(19),функцииперемещенияразлагаютсявряд

Маклорена:

(k)

(k) z

(k) z i

= B0

+ B1

+ B2

+ B3

+ ...+ Bi

+ ..., (k = 1,2)

(20)

= A0

+ A1

+ A2

+ A3

+ ...+ Ai

+ ...

(21)

Здесь B (k), - неизвестные функции двух про-

Вычитая два первых уравнения (9) из двух

странственных координат Bi(k) = Bi(k) (x1, x2, t), (i =

уравнений системы (8), получим следующие два

1,2,3,...)

уравнения:

Используя соотношения (1) - (4), (6) и ряды

Маклорена (20), (21), получим выражения неиз-

вестных функций

выражений (13),

(15)

Rk , a 1, a 1, R, a

(14), которые определяют бимоменты

здесь бимоменты

определяются

по формулам

ВЫСШАЯ ШКОЛА • №23 / 2023 47

Физико-математические науки

Таким образом, были построены две независи-

Где

мые системы по три уравнения движения толстой

пластины, в каждой из которых содержится по три

неизвестных функции перемещений лицевых по-

верхностей пластины

2, W и u~1, u~2, W .

Приведемформулыдляопределенияперемеще-

ний и напряжений на лицевых поверхностях пла-

(23)

стины z = h и z = +h:

i u~i ,

i + u~i , (i

ui( ) =

ui(+) =

= 1,2),

u3(

) = W W ,

u3(+)

s ij( ) = s

ij s~ij ,

s ij(+) = s

ij +s~ij ,

(i =

1,2; j = 1,2).

= W + W .

(24)

Аналогично,используясоотношения(1)-(3),(6) и ряды Маклорена (20), (21), получим выражения

неизвестных функций ~ ~ ~ ~ ~ ~ выра-

R1, R2, a 1, a 1, R, a

жений (18), (19), которые определяют бимоменты

(28)

Граничные условия бимоментной теории пластин. Граничные условия бимоментной тео- рии пластин описываются относительно обобщен- ных функций перемещений и силовых факторов, т.е. относительно напряжений лицевых поверхно- стей (11), ( 16) и сил, моментов, бимоментов [5, 6].

Если на границе пластины перемещения равны нулю, то граничные условия для уравнений на

краю x1 = const имеют вид:

= 0,

y 1

y 2

r =

g = 0,

W = 0,

= 0,

2 = 0, b1 = 0, b2 = 0, r = 0, g

= 0,

u1 = 0,

2 = 0, W = 0.

y 1

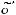
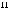
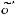в виде

Где

(26)

(27)

	(29)
(25)	Если край пластины оперт, то на краю x1 = const
(25)	имеем граничные условия, которые имеют вид:

(30)

Если край пластины оперт и имеется диафраг- ма, которая стесняет перемещение по касательно-

му направлению к контуру, то на краю x1 = const условия имеют вид:

(31)

Для свободного края пластины x1 = const гра- ничные условия будут представлены в виде:

Здесь необходимо отметить, что приближен-

(32)

Пример. Приведем результаты динамического

ныевыражения(23),(24),(26),(27)имеютвысокую

расчета толстой пластины, находящейся под дей-

точность и построены с шестым порядком точно-

ствием распределенной по синусоидальному зако-

сти

относительно малого параметра пластины

ну динамической нагрузки в виде

. Здесь a - малый размер в плане пластины.

Отметим, что были построены выражения

бимоментов для симметричной и асимметричной

где q0 – параметр внешней нагрузки.

задач(22)и(25),которыеявляютсячленамисисте-

мы уравнений (10), (12) и (15), (17), соответствен-

Обобщенные перемещения пластины симме-

но, для определения шести неизвестных функций

тричной и асимметричной задач, удовлетворяю-

щие граничным условиям (31), представим в виде:

и u~1, u~1, W .

ВЫСШАЯ ШКОЛА • №23 / 2023

Физико-математические науки

y 1 = f1(x1,x2)j 1

(t),

= f2(x1,x2)j

2(t),

= f3(x1,x2)j

3(t),

y 2

b1 = f1(x1,x2)j 4

(t),

= f2(x1,x2)j 5(t),

= f3(x1,x2)j 6(t),

(t),

(t).

= f (x ,x )j

= f (x1,x )j

= f (x ,x )j

(34)

Координатныефункциидляшарнирноопертых пластин имеют вид

f1(x1,x2)= cos(pax1)sin(pbx2 ); f2(x1,x2)= sin(pax1)cos(pbx2 ); f3(x xb2 ); f3(x1,x2)= sin(pax1)sin(pbx2 )

После разделения переменных в виде (33) и (34) получим две системы обыкновенных диффе- ренциальных уравнений движения пластины от-

носительно функций	времени j 1(t), j 2(t),...,j 9(t)
и j~1(t), j~2(t),...., j~9(t)	для первой и второй задач,

соответственно, которые решены по явной схеме методом конечных разностей при нулевых началь- ных условиях.

Расчеты проведены для квадратной ортотроп- ной пластины СВАМ 15:1 со следующими характе-

ристиками:E1 = 4.6∙E0,E2 = 1.6∙E0,E3 = 1.12∙E0,модули

сдвигов:G12 = 0.56∙E0,G13 = 0.33∙E0,G23 = 0.43∙E0,гдеE0

= 104МПа и коэффициенты Пуассона: v21 = 0.27, v31 = 0.3, v23 = 0.07.

Приведем результаты расчетов для квадратной ортотропной пластины с размерами a = b = 3H; 4H; 5H.

Введены безразмерные нормальные обобщен- ное перемещение ~r и нормальные перемещения u3(-) и u3(+) на лицевых поверхностях пластины z = -h и z = +h по формулам

Максимальные значения нормальных напря- жений на лицевых поверхностях пластины z = -h и z = +h достигаются в точке ортотропной пластины x1 = a /2, y1 = b/2, а максимальные значения каса-

тельных напряжений σ12(-), σ12(+), - в точке пластины x1 = 0, y1 = b/2.

В табл. 1 и 2 приведены численные результаты расчета безразмерных кинематических функций и напряжений для ортотропной пластины, полу- ченныепобимоментнойтеории(см.табл.1)ипоте- ории Тимошенко (см. табл.2). Установлено, что по теории Тимошенко числовые значения напряже- ний получаются значительно меньшими по срав- нению с бимоментной теорией пластин.

На основе анализа численных результатов сде- ланвыводотом,чтопотеорииТимошенкозначения перемещений и напряжений пластины получают- ся значительно меньше. Максимальные значения нормальных напряжений ортотропной пластины, полученные по бимоментной теории, до 40% боль- ше, чем полученные по теории Тимошенко.

Таблица 1

Максимальные значения нормальных перемещений и напряжений в пластине

H /a	~	( )	(+)	(	)	(	)	( )	(+)
H /a	r	u3	u3	s 1		s 1+		s 2	s 2
1/3	5.112	5.411	5.016	–7.073		6.579		–4.179	3.814
1/4	12.169	12.388	11.979	–11.113		10.872		–6.063	5.825
1/5	24.121	24.652	24.120	–16.968		16.742		–8.501	8.490

Таблица 2

Максимальные значения нормальных перемещений и напряжений в пластине

	H /a	~	( )	(+)	( )	(+)
	H /a	r	s 1	s 1	s 2	s 2
	1/3	4.828	–5.134	5.134	–3.291	3.291
	1/4	11.602	–9.541	9.541	–5.235	5.235
	1/5	24.074	–15.336	15.336	–7.702	7.702
Выводы. На основе бимоментной теории пла-				Отметим, что преимущество бимоментной те-
стин проведен динамический расчет ортотропной				ории среди существующих теорий заключается
пластины при действии поперечного динамиче-				в высокой точности и в хорошей применимости
скоговоздействия.Полученычисленныерезульта-				при решениях различных практических задач для
ты перемещений и напряжений для опертых пла-				оценки напряжений и перемещений толстых пла-
стин. На основе анализа численных результатов				стин и пластинчатых сооружений при динамиче-
сделан вывод о том, что максимальные значения				скихвоздействиях.
нормальных напряжений ортотропной пластины,

полученные по бимоментной теории, значительно	ВЫСШАЯ ШКОЛА • №23 / 2023	49
больше, чем полученные по теории Тимошенко.	ВЫСШАЯ ШКОЛА • №23 / 2023	49
больше, чем полученные по теории Тимошенко.

Физико-математические науки

Список использованных источников

1.С.А. Амбарцумян. Теория анизотропных пластин. –М. Наука. Гл. ред. физ.-мат. лит. 1987. 360 с.

2.В.И. Горбачев. Об одном подходе к построению теории пластин. М. Изд. МГУ, Упругость и неупругость, 2006. С. 301-310.

3.А.Б. Ахмедов. Действие сосредоточенных сил на упругую плиту // Узбекский журнал Проблемы механики. Ташкент. №4. 2006. С.5-9.

4.Си-Хунг Чанг, Цзянн-Куо Тарн. Трехмерные решения упругости прямоугольных ортотропных пластин. Журнал эластичности. 2012. Том. 108. №1. С. 49-66.

5.М.К. Усаров. Задача изгиба для толстой ортотропной пластины в трехмерной постановке. Санкт-Петербург// Инженерно-строительный журнал. №4. (22). 2011. С.40-47.

6.Усаров М.К. Изгиб ортотропных пластин с учетом бимоментов. Санкт-Петербург // Инженерно-строительный журнал. №1. (53). 2015. С.80-90.

7.Мakhamatali K. Usarov «Dynamic Design of Thick Orthotropic Cantilever Plates with Consideration of Bimoments», World Journal of Mechanics, 2016, 6. Р. 341-356.

8.Usarov, D., Turajonov, K., Khamidov, S. Simulation of free vibrations of a thick plate without simplifying hypotheses. Journal of Physics: Conference Series. 2019. 1425. Pp. 012115. DOI:10.1088/1742-6596/1425/1/012115. https://iopscience. iop.org/article/10.1088/1742-6596/1425/1/012115.

9. Mirsaidov, M., Usarov, M. Bimoment theory construction to assess the stress state of thick orthotropic plates. IOP Conference Series: Earth and Environmental Science, 2020, 614(1), 012090, https://doi.org/10.1088/17551315/614/1/012090.

50 ВЫСШАЯ ШКОЛА • №23 / 2023

<<< < Предыдущая 1 2 3 45 / 65 6 > Следующая >>>

Соседние файлы в папке книги2

#
25.02.20243.5 Mб0333-1.pdf
#
24.02.20244.03 Mб0333.pdf
#
24.02.20242.21 Mб0333602444.pdf
#
24.02.20241.4 Mб0335.pdf
#
24.02.20243.43 Mб1336.pdf
#
25.02.20243.47 Mб0337.pdf
#
24.02.20243.39 Mб0338.pdf
#
24.02.20242.04 Mб0339.pdf
#
25.02.20245.29 Mб034-1.pdf
#
24.02.20243.17 Mб034.pdf
#
25.02.20241.43 Mб0341-1.pdf