
«Дополнительные главы ТОЭ» Лекция 1
Применение численных методов при расчете переходных процессов в электрических цепях
Доцент ВШВЭ Е.Ю.Кочеткова

ЛИТЕРАТУРА
К.С. Демирчян, Л.Р.Нейман, Н.В.Коровкин, В.Л.Чечурин, Теоретические основы электротехники, 4-е издание, тт. 1,2
Одним из общих методов расчета переходных процессов в электрических цепях, ориентированных на использование численного решения системы дифференциальных уравнений, является метод переменных состояния.
Итогом формирования системы уравнений состояния (а следует отметить, что ее формирование представляет собой весьма трудоемкую задачу) является матричное уравнение:
dX |
AX F (t) |
|
|
dt |
|
X (t |
) X |
0 |
0 |
|
где Х – вектор неизвестных переменных состояния (токи катушек и напряжения конденсаторов), А – матрица, элементы которой определяются через параметры цепи (R,L,C), F(t) – вектор, элементы которого учитывают вклад источников, действующих в цепи. Система дифференциальных уравнений в совокупности с начальными условиями представляет так называемую задачу Коши
:

Для использования стандартных методов численного интегрирования обыкновенных дифференциальных уравнений интегрируемая система должна быть записана в нормальной форме
dx j dt f j (x1, x2 ,...xn ,t), j 1,2,...n
Именно к такому представлению приводит метод переменных состояния.
Основой используемых численных методов является вычисление
приращений переменной состояния x j x j |
(tk 1 ) x j |
(tk ) |
|
за некоторый |
|||
промежуток времени - шаг интегрирования: |
t |
k |
t |
k 1 |
t |
k |
h |
Таким образом , решение уравнения получаем в виде таблицы значений хj, соответствующих отдельным моментам времени, с интервалом h.
Для вычисления значений хj дифференциальное уравнение заменяют алгебраическим уравнением, называемым разностным уравнением, которое может быть построено с помощью формулы Ньютона-Лейбница
x tktk 1 f (x,t)dt
(индексы j у переменных х и f опущены)
Методы численного интегрирования различаются по способу аппроксимации подынтегральной функции в последнем выражении. Наиболее простой вид имеют формулы:
явного метода Эйлера |
x fk |
(xk , tk )h fk h |
|
вкотором подынтегральная функция f принимается равной ее значению fk
вначале промежутка интегрирования . Этот метод соответствует приближенному вычислению интеграла по способу левых прямоугольников
неявного метода Эйлера
x f |
k 1 |
h |
|
|
в котором подынтегральная функция f принимается равной ее значению fk+1 в конце промежутка интегрирования. Этот метод соответствует приближенному вычислению интеграла по способу правых прямоугольников
метода трапеций (неявный метод)
x ( f |
k |
f |
k 1 |
)h / 2 |
|
|
|
когда подынтегральная функция f аппроксимируется полусуммой ее значений в начале и в конце промежутка

Отметим, что в явном методе используются значения fk (xk , tk ) которые находятся на основе уже вычисленных на предыдущем шаге
значений хk |
|
|
|
Неявные методы используют значения |
f |
k 1 |
, неизвестные в начале |
|
|
|
вычислений на каждом шаге. Отсюда – их название. Их реализация более сложна, т.к. она требует на каждом шаге интегрирования решения системы алгебраических уравнений относительно неизвестных значений хk 1 в конце данного шага.
Устойчивость методов численного интегрированияx
Для знакомства с понятием устойчивости соответствующего метода численного интегрирования рассмотрим дифференциальное уравнение
dx dt x, x(0) x0 1
Его решение x(t) x0e t
x(tk ) x0e kh
В соответствии с явным методом Эйлера
x |
|
x |
x h x (1 h) |
|
|||
1 |
0 |
0 |
0 |
|
|
|
|
x |
|
x |
x h x (1 h) |
|
|||
|
|
|
|
|
|
2 |
|
|
2 |
1 |
1 |
0 |
|
|
|
x |
|
x |
(1 h) |
k |
|
|
|
k |
|
|
|
|
|||
|
0 |
|
|
|
|
|
|
Если (с учетом λ <0) h имеет такое значение, что |1+λh |>1, то |
|||||||
абсолютное значение решения |
x |
k |
увеличивается, тогда, как точное |
||||
|
|||||||
решение убывает с ростом k. В данном случае применение явного метода Эйлера связано с потерей устойчивости решения.
Таким образом, при применении явного метода Эйлера является необходимым выполнение условия |1+λh |<1 для всех собственных чисел матрицы А, что при больших по модулю λ ведет к требованию значительного уменьшения шага h.
Применим разностное уравнение неявного метода Эйлера:
x1 x0 x1h x1 x0 /(1 h) x2 x1 x2 h
x2 x1 /(1 h) x0 (1 h) 2 xk x0 (1 h) k
Для обеспечения устойчивости решения данного уравнения необходимо,
чтобы |
(1 h ) 1 1 |
А это значит, что неявный метод Эйлера устойчив для любых значений λ. |
|
В общем случае , когда собственные числа матрицы А имеют вид λ=α+jω, условие устойчивости может быть записано: (1-hα)2 +(hω)2 >1, и оно выполняется, т.к. Re[λ]≤ 0 (см.свойства корней характеристического уравнения)
Жесткость систем дифференциальных уравнений электрических цепей
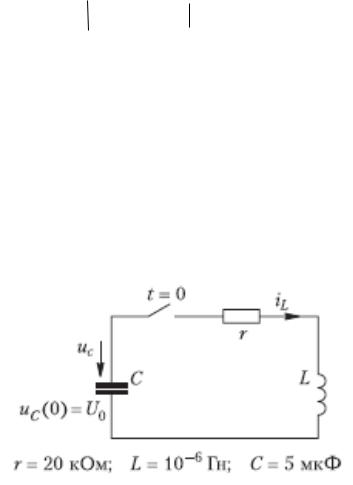
Рассмотрим пример: разряд конденсатора на цепь R,L (рис.1)
R
рис.1
(Обратим внимание на соотношение параметров: L/R <<RC)
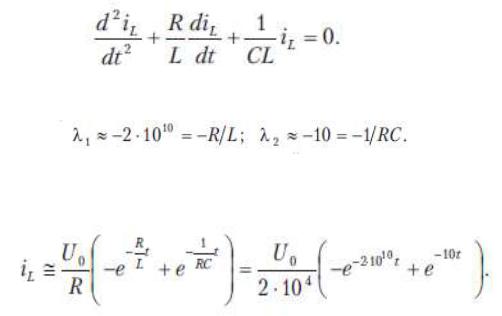
Зависимость тока в цепи от времени может быть получена из решения дифф.уравнения
Корни характеристического уравнения:
Решение дифференциального уравнения (с учетом начальных условий) имеет вид
График тока условно изображен на рис.2. На нем можно выделить 2 участка.
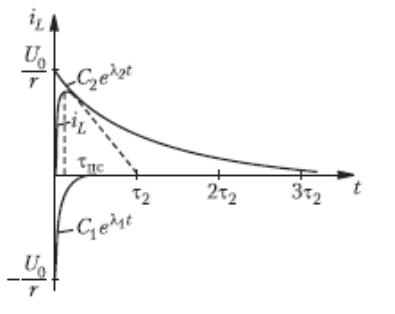
рис.2
1-й участок – пограничный слой (от t=0 до t = τпс), характеризуется быстрым изменением тока. Длительность его: τпс = 3 τmin =3|1/λ1|
Эта фаза переходного процесса соответствует процессу в цепи на рис. 3а 2-й участок –за пограничным слоем , характеризуется медленным изменением тока. Длительность его определяется максимальной постоянной времени τmax =|1/λ2|. Обычно переходный процесс рассматривают на интервале 3 τmax . Эта фаза переходного процесса соответствует процессу в цепи на рис. 3б.
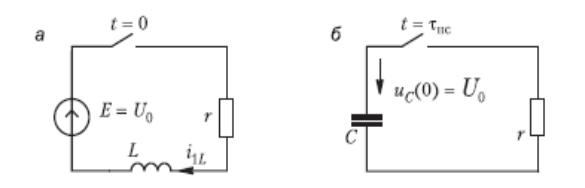
рис.3
Необходимость использования таких функций (одна -очень быстрая, другая - очень медленная) в решении дифференциальных уравнений характеризует явление жесткости. Это явление типично для задач теории электрических цепей. Численное решение жестких дифференциальных систем с помощью явного метода затруднительно.
Согласно критерию устойчивости явного метода Эйлера, в данном случае h<10-10с, а длительность переходного процесса (см.выше) равна 3 τmax =0,3с. Нетрудно посчитать, сколько шагов потребовало бы получение численного решения уравнения явным методом.
Иначе дело обстоит с использованием неявных методов. Однако, как отмечалось выше, реализация неявных методов более сложна.
