Вопросы, выделенные курсивом, готовить без доказательств!!!

1. (Алина) Первообразная и неопределенный интеграл (определения, свойства).

Пусть имеется функция 𝑓, определена на промежутке <а,𝑏>

Опр: дифференцируемая на <а,𝑏> функция 𝐹(𝑥) называется первообразной функции 𝑓(𝑥), если 𝐹′(𝑥)=𝑓(𝑥).

Теорема 1:

1) Если функция 𝐹(𝑥) – первообразная для 𝑓(𝑥), то функция 𝐹(𝑥)+С – первообразная для 𝑓(𝑥)

2) Любые две первообразные одной функции отличаются на 𝑐𝑜𝑛𝑠𝑡.

Док-во:

1) (𝐹(𝑥)+С)′= 𝑓(𝑥)

2) Пусть функции 𝐹1,𝐹2 – первообразные для функции 𝑓

Рассмотрим функцию 𝜑(𝑥)=𝐹1(𝑥)−𝐹2(𝑥)

𝜑′(𝑥)=𝐹1′(𝑥)−𝐹2′(𝑥)=𝑓(𝑥)−𝑓(𝑥)=0 (для всех точек <а,𝑏>)

Пусть 𝑥1,𝑥2 ∈ <а,𝑏> (𝑥1<𝑥2 )

𝜑(𝑥2)−𝜑(𝑥1)=(по т.Лагранжа) 𝜑′(с)∗(𝑥2− 𝑥1)=0 с∈(𝑥1,𝑥2) ⇒ 𝜑(𝑥1)=𝜑(𝑥2) ⇒ 𝜑(𝑥)≡𝐶

⇒𝐹1(𝑥)=𝐹2(𝑥)+𝐶 ч.т.д.

Опр: Множество всех первообразных функции 𝑓 на <а,𝑏> называется неопределённым интегралом от функции 𝑓(𝑥) и обозначается ∫𝑓(𝑥) 𝑑(𝑥) (интеграл от 𝑓 от 𝑥 𝑑(𝑥))

Таким образом ∫𝑓(𝑥) 𝑑(𝑥)= 𝐹(𝑥)+С, С− произвольная постоянная, 𝑑(𝑥) – указывает по какой переменной берётся интеграл

2. (Карина) Интегрирование по частям и замена переменной.

Интегрирование по частям:

Теорема 1: Пусть функции дифференцируемы на , а функции имеется первообразная на этом промежутке. Тогда (формула интегрирования по частям)

Док – во:

(

ч.т.д

Замечание: Перепишем Т1 в виде: (правило интегрирования по частям)

Замена переменной:

Теорема 1: Пусть 1) функция имеет первообразную на

2) функция определена и дифференцируема на и (при чём, если подействуем функцией фи на промежуток (найдем образ под действием функции ), то этот образ обязан содержаться на промежутке , тогда

Док – во: Пусть – первообразная для функции , то есть

Рассмотрим сложную функцию ( – первообразная для функции . Ч.т.д.

Пример:

Замена: пусть

3. (Геля) Интегрирование рациональных функций.

Опр: Функция 𝑓(𝑥) называется интегрируемой в элементарных функциях, если её первообразная является элементарной функцией. Рациональная функция- функция равная, отношению двух многочленов

𝑃(𝑥)/𝑄(𝑥) интегрируема в элементарных функциях

𝑃(𝑥)/𝑄(𝑥)-правильная дробь(т.е. числитель меньше знаменателя)

Всякая правильная дробь может быть представлена в виде простейших дробей.

К простейшим относятся дроби вида:

В 3 и 4 знаменатели не имеют корней

Вычисление 𝑃(𝑥)/𝑄(𝑥)dx сводиться к вычислению интегралов от функций 1-4

𝑃(𝑥)/𝑄(𝑥)−неправильная дробь

𝑃(𝑥)/𝑄(𝑥)=М(х)−остаток+𝑅(𝑥)/𝑄(𝑥) обе части интегрируются в элементарных функциях=> сама дробь будет интегрироваться в элементарных функциях

4. (Алина) Интегрирование иррациональных функций , биномиальный дифференциал, подстановки Эйлера).

Идея: с помощью замены привести подынтегральную функцию к рациональной.

1. , где R(x,y) – рациональная функция,

Теорема 1: – вычисляется в элементарных функциях

Док – во:

Замена:

– рациональная функция

– рациональная функция

Интегрируема в элементарных функциях ч.т.д.

2. Биномиальный дифференциал (дифференциальный бином)

– вещественные

– рациональные

Теорема 2: Если выполняется одно из трёх условий:

1) – степень – целое число

2) – целое число

3) – целое число,

То вычисляется в элементарных функциях

Док – во:

Замена: об.:

=

Функция из 1) замена

2)

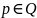
По 1) замена:

3)

По 1) замена:

ч.т.д.

Замечание 1: П.Л.Чебышёв доказал, что в других случаях биномиальный дифференциал не интегрируется в элементарных функциях (без доказательств)

Замечание 2: Из доказательства теоремы 2 следует

Замена: – знаменатель дроби , то есть дроби

2)

Замена: d – знаменатель дроби p

3)

Замена: – знаменатель дроби p

3. Подстановка Эйлера

(не имеет одинаковых корней)

Теорема: Если не выполняется хотя бы одно из условий: 1) 2) 3) , имеет два различных корня, то (1) будет вычисляться в элементарных функциях

Док – во: 1)

Замена: (знаки можно выбирать любые)

x=x (t) рац.

1. 

Интеграл от рациональной функции (1) вычисляется в элементарных функциях

2)

Замена:

Интеграл от рациональной функции (1) вычисляется в элементарных функциях

3)

– разные

Замена:

Интеграл от рациональной функции (1) вычисляется в элементарных функциях