Ekz_progr_po_TViMS_dlya_IE (1)

Где = ( 1), ( 1) = -

Замечание:

Существует, в настоящее время, много вариантов формулировок центральной предельной теоремы, но суть их одна:

-Величины должны быть независимы (слабо зависимы)

-Каждая из них, по сравнению с суммой, мала

15.3Следствия:

закон распределения близкий к нормальному:

16. Понятие о законе больших чисел. Примеры проявлений его. Неравенство Чебышева. Теорема Чебышева. Теорема Бернулли.

16.1 Закон больших чисел:

Закон больших чисел формулирует условия, при которых совокупное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая.

Наиболее зримой иллюстрацией действия закона больших чисел служит постоянство давления газа. Каждая молекула газа, двигаясь хаотично, в случайные моменты времени сталкивается со стенкой сосуда, в котором газ заключен. Из-за большого числа молекул, давление газа как суммарный итог соударений молекул со стенками сосуда практически остается постоянным.

16.2 Неравенство Чебышева:

Пусть имеет ( ) и ( ) ( ) < ∞. Тогда, каково бы ни было > 0

слагаемых, в которых | 1 − ( )| < , сумма может только уменьшиться:

Если в оставшейся сумме каждое выражение | 1 − ( )| заменить , то от этого сумма разве что уменьшиться, так как | 1 − ( )| ≥ . В итоге

|7%&'(?)|GH |7%&'(?)|GH

Разделив на - обе части данного выражения, получим желаемое неравенство

Определение:

Говорят, что последовательность случайных величин ,, -, … , " сходится по вероятности к постоянной величине , если для любого > 0 выполняется:

(наблюдений) среднее арифметическое их результатов сходится по вероятности к математическому ожиданию случайной величины

Доказательство:

Рассмотрим ¦ = ∑#%)!" ?% – среднее арифметическое

(| ¦ − ( )| < ∞) ≥ 1

"→:

Но вероятность не может быть больше единицы, поэтому неравенство можно заменить на равенство

Замечание 1:

Теорема Чебышева обосновывает возможность определения математического ожидания случайной величины по результатам наблюдений.

Замечание 2:

Пусть измеряется некоторая постоянная величина . При измерении допускается некоторая ошибка , и в результате измерений получается величина + . Если систематических ошибок нет, т.е. ( ) = 0, то( + ) = ( ) + ( ) = ( ) = . Это означает, что при достаточно большом числе измерений среднее арифметическое их результатов будет сколь угодно близко к с вероятностью, как угодно близкой к единице.

16.4 Теорема Бернулли:

При неограниченном увеличении числа независимых опытов частота события сходится по вероятности к вероятности этого события: > 0

можно заменить на равенство

17. Статистическая и функциональная зависимости. Корреляционная зависимость. Линия регрессии. Свойство линии регрессии минимизировать среднюю квадратическую ошибку прогноза.

17.1 Статистическая и функциональная зависимости.

Функциональная зависимость – зависимость, при которой каждому значению аргумента соответствует строго определенное значение функции

Статистическая зависимость проявляется в том, что закон распределения одной случайной величины изменяется при изменении другой. Если – дискретная случайная величина, то это означает, что при каждом фиксированном значении = имеется набор возможных значений и соответствующим им условных вероятностей 7( ) = ?27( = ).

Набор возможных значений и соответствующих им условных вероятностей образует условный закон распределения:

J 7( ) = 1

L

Условный закон распределения имеет числовые характеристики такие же, как и обычные законы распределения. Например, 7( ) = ∑L 7( ) – для дискретной случайной величины называют условным математическим ожиданием или средним значением при заданном значении = .

Для непрерывной случайной величины: 7( ) = ∫&:: 7( )

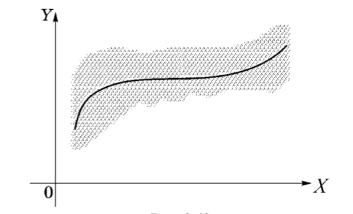
17.2 Линия регрессии.

Если условные математические ожидания при разных значения соединить, то получается линия, которая называется линией регрессии на

17.3 Корреляционная зависимость

Корреляционной зависимостью от называется функциональная зависимость условного среднего значения от . Графиком корреляционной зависимости служит линия регрессии

17.4Свойство линии регрессии минимизировать среднюю квадратическую ошибку прогноза

7-( ) = ∑L( − 7( )- 7( ) – условная дисперсия при данном =

Если в качестве предполагаемого значения взять 7( ), то 7-( ) – средний квадрат ошибки прогноза, при =

?-( ) = ∑7 7-( ) ( = ) – средняя из условных дисперсий. Эта величина характеризует средний квадрат разброса относительно линии регрессии. Ее можно записать в виде: ?-( ) = [ − ?( )]-

( − )- = [ − ( ) + ( ) − ]- = = [ − ( )]- + 2[ ( ) − ] [ − ( )] + [ ( ) − ]-.

Второе слагаемое [ − ( )] = ( ) − ( ) = 0. Третье слагаемое, очевидно неотрицательно. Поэтому:

( − )- ≥ [ − ( )]-

Равенство возможно лишь при = ( ). Это означает, что средняя квадратическая ошибка прогноза будет наименьшей, если случайную величину прогнозировать по ее среднему значению. Так как линия регрессии проходит через условные средние значения , то можно утверждать, что линия регрессии минимизирует среднюю квадратическую ошибку прогноза случайной величины по наблюдаемому значению величины

18. Коэффициент корреляции и свойства. Оценка параметров линейной корреляции на основе опытных данных.

18.1 Коэффициент корреляции и его свойства

Для характеристики зависимости между и используют величину,

7L = ( , ) = 4 ̇̇5 = ª( − 7)( − L)«

Которая называется ковариацией Из определения ковариации:

( , ) = ª − L − 7 + 7 L« = = ( ) − ( ) ( )

Откуда

( ) = ( ) ( ) + ( , )

Для дисперсии:

( ± ) = ( ) + ( ) ± 2 ( , )

Однако значения ( , ) изменяются при изменении единиц измерения и . Поэтому для характеристики зависимости между величинами удобно рассматривать безразмерную величину, называемую коэффициентом корреляции:

Коэффициент корреляции показывает, насколько статистическая зависимость близка к линейной функциональной зависимости

Свойства:

-Т.к ?-( ) ≥ 0, то 1 − 7L- ≥ 0 => 7L- ≤ 1 => −1 ≤ 7L ≤ 1

-Если 7L = 0, то линия регрессии параллельна оси . В этом случае говорят, что величины некоррелированны, так как среднее значениене изменяется при изменении

-Если 7L > 0, то говорят, что величины коррелированы положительно

-Если 7L < 0, то говорят, что величины коррелированы отрицательно

-Если 7L = ±1 => ?-( ) = 0 – разброса относительно линии регрессии нет, величины связаны линейной функциональной зависимостью

-При ?-( ) → 0 ® 7L® → 1 – это значит, что чем больше по модулю коэффициент корреляции тем меньше разброс относительно линии регрессии

18.2Оценка параметров линейной корреляции на основе опытных данных:

Пусть ( , ) – пара случайных величин Полагаем ?( ) = + – вид линии регрессии Согласно свойству линии регрессии:

( − − )- = ( , )

Для нахождения параметров и используем необходимое условие экстремума, т.е. ;( , ) = 0

Тогда:

= 2 ( − − )(− ) = 0

= 2 ( − − )(−1) = 0

± ( -) + ( ) = ( )

( ) + = ( )

Решение этой системы имеет вид:

= ?M M , = ( ) − ?M M ( )? ?

19. Предмет математической статистики. Точечные оценки. Оценки несмещенные и состоятельные. Оценки для математического ожидания и дисперсии.

19.1 Предмет математической статистики

Математическая статистика – наука о методах получения научно обоснованных выводов о случайных явлениях по результатам их наблюдений

Выборка должна быть репрезентативной (представительской)

-Для этого она должна быть достаточно большого объема

-Нужно обеспечить равные шансы попасть в выборку для всех элементов генеральной совокупности

Разделы математической статистики:

-Теория оценивания

-Проверка статистических гипотез

-Корреляционный анализ на основе опытных данных

19.2Точечные оценки. Оценки несмещенные и состоятельные.

Пусть случайная величина имеет неизвестную характеристику

,, -, … , " – результаты наблюдений Функция результатов наблюдений ² = ²( ,, -, … , ") называется

точечной оценкой, если ее значения близки к неизвестному значению Естественные требования к оценке:

-Оценка ² называется несмещенной, если ее математическое ожидание равно оцениваемой величине: (²) = . В противном случается говорят, что оценка смещенная

-Оценка ² называется состоятельной, если она сходится по вероятности к оцениваемой величине, то есть:

> 0 (|²( ,, -, … , ") − | < ) = 1

"→:

Оценка, построенная по большему числу наблюдений, вообще говоря, более точна