
TM_Lectures_part_I_15
.pdf
Лекция 15 (ТМ, часть I)
Задача Кеплера
Задача Кеплера – это задача об описании движения тела под действием гравитационной или электростатической силы.
Эти силы имеют подобный вид (они являются центральными, а их амплитуда обратно пропорциональна квадрату расстояния между взаимодействующими телами):
|
|
m m |
|
|
|
|
|
|
||||
F |
1 |
|
2 |
r |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||||
гр |
|
|
r |
3 |
|
|
1,2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
||||
|
|
|
1,2 |
|
|
U r |
|
|||||
|
|
|
|
|
||||||||
|
|
q q |
|
1,2 |
|
r |
||||||
|
|
|
|
|
|
|
|
|
|
|||
F |
|
|
1 |
|
|
2 |
r |
|
|
|
||
|
|
3 |
|
|
|
1,2 |
||||||
кул |
|
r |
|
|
1,2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
1,2 |
|
|
|
|
|
|
|||
.
Опираясь на эти выражения, мы можем записать потенциальную энергию в общем виде, так как это показано выше. Константа определяет характер взаимодействия, она содержит либо произведение масс тел m , либо их зарядов q помноженные на соответствующие константы.
Задача Кеплера является частным случаем задачи о движении тела в центрально-симметричном поле. Т.е. является иллюстрацией конкретного решения этой задачи.
Зная выражение для потенциальной энергии (рекомендуется вспомнить Лекцию №13 о движении в одномерном случае и № 14), мы легко можем получить эффективную потенциальную энергию:
|
|
|
|
|
|
|
U |
|
r |
|
|
2 |
|
eff |
|
0 |
|
|||
|
|
|
|
|
||
|
|
|
r |
|
2mr |
2 |
|
|
|
|
|
, (1)
которая определяет характер движения в системе. Здесь Mo – значение начального момента импульса.
Поскольку рассматриваемые силы являются центральными, то движение тела всегда происходит в фиксированной плоскости, которая определяется начальными условиями (т.к. выполняется закон сохранения момента импульса, см. Лекцию №9 и № 14).

Рассмотрим возможные области движения. Если константа <0. То эффективная потенциальная энергия всюду положительная с отталкивающим потенциальным барьером в окрестности r = 0. На бесконечности она обращается в ноль.
Область движения ограничена одной точкой поворота 1, и имеет инфинитный характер.
Если константа > 0, то в этом случае эффективная потенциальная энергия имеет потенциальную яму там где .
| |
|
| > |
|
|
, |
|
2 |
2 |
|||
|
|
|
|
Что определяется силовой константой , массой тела и значением момента импульса Mo. При этом в области r = 0 эффективная потенциальная энергия имеет отталкивающий потенциальный барьер, а на бесконечности она обращается в ноль. Таким образом значение полной энергии системы Eo
будет определять границы области движения.
Можно выделить четыре случая:
I. E0 0 , движение неограниченно (инфинитное, одна точка поворота);
II. Eo = 0, движение неограниченно (инфинитное, две точки поворота, вторая точка находится на бесконечности);
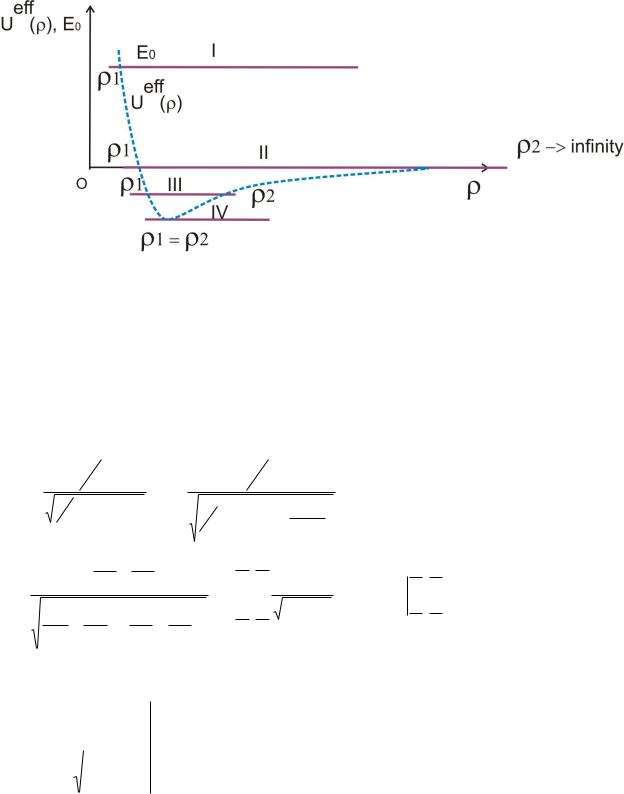
III. E0 |
0 , движение ограничено (финитное, две точки поворота); |
|
III. E0 |
Umin |
, движение происходит по круговой траектории (положения 2х |
|
eff |
|
точек поворота совпадают).
См. рисунок ниже:
Решение задачи мы можем получить, используя результаты предыдущей Лекции № 14, где мы получили квадратуры для задачи о движении тела в центрально-симметричном поле.
Подставляя (1) в квадратуру для траектории и выполняя интегрирование имеем общее решение:
r |
|
0 |
|
|
|
r |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
||||
|
|
mr |
|
|
|
|
|
mr |
|
|
|
|
|||||
|
|
|
|
|
dr |
|
|
|
|
|
|
dr |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2 |
E U |
eff |
|
|
|
|
|
|
|
|
2 |
|
|||||
r |
r |
2 |
|
|
|
|
|
||||||||||
i |
m |
|
0 |
|
|
|
i |
E |
|
|
|
0 |
|
|
|||
|
|
|
|
|
|
|
m |
|
|
|
|
|
2 |
|
|||
|
|
|
|
|
|
|
|
|
0 |
|
r |
|
2mr |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
M |
0 |
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
||||
r |
|
|
|
|
|
|
M |
|
|
|
|
mr |
|
M |
0 |
d |
|
|
|
||||
|
|
|
|
mr |
|
0 |
|
|
|
|
|
|
|
|
arccos |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
A |
|
|
|
A |
||||
r |
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|||||
|
2E |
|
|
|
|
M |
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
2 |
|
|
|
i |
0 |
|
|
0 |
|
|
1 |
|
|
0 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
mr |
|
|
|
|
|
|
|
|
|||||||
|
m |
|
|
M 0 |
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mr |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||||||
M |
0 |
|
|
|
|
|
|
|
|
mr |
|
M |
0 |
|
|
|
|
|
|
M |
0 |
|
|
|
|
|
|
|
|
mr |
|
M |
0 |
|
|
1 |
|
|
|
или
|
|
M 0 |
|
|
|
r |
|
||||||
arccos |
|
mr |
|
M 0 |
|
|
|
|
. |
||||
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
M 0 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||
|
|
|
mr |
|
M 0 |
|
|
r1 |
|
||||
|
|
|
|
|
|
|
|
|
|||||
Здесь r1 – точка поворота.

Введем следующие величины:
p |
02 |
, |
|
m |
|||
|
|
Тогда
|
|
2M |
2 |
E |
|
|
1 |
0 |
|||
|
|
||||
|
|
|
|
||
|
|
m |
2 |
||
|
|
|
|
||
.
|
1 |
|
|
arccos |
|
1 |
|
|
|
|
p r
,
Что позволяет получить окончательный вид для траектории движения:
r |
p |
|
|
1 |
cos |
|
|
. (2)
Из данного выражения видно, что расстояние от центра поля может иметь минимальное и максимальное значение в зависимости от параметра
(эксцентриситет). В свою очередь, если фиксировать Mo, m и силовой параметр, значение энергии системы может влиять на вид траектории.
Возможны четыре варианта:
Если 1 |
(E > 0), то возможные траектории движения – гиперболы. |
Если 1 |
(E = 0) - параболы. |
Если 1 (E < 0) - эллипсы. |
|
Если 0 |
(E = Ueff) - окружности. |
См. рисунок ниже
Задача Кеплера описывает движение планет, искусственных спутников и других физических тел движущих под действием гравитационной и электростатической силы.
