Министерство науки и высшего образования Российской Федерации

Федеральное государственное бюджетное

образовательное учреждение высшего образования

«Ярославский государственный университет им. П.Г. Демидова»

(ЯрГУ)

Физический факультет

наименование факультета

Лабораторная работа №1

Наименование работы: Гармонический анализ сигналов

Студенты группы РФ-21БО

«__» 2021г.

Ярославль 2021г.

Содержание

2 Ход работы 10

2.1 Теоретическая часть 10

2.1.1 Прямоугольный сигнал 10

2.1.2 Треугольный сигнал 11

2.1.3 Трапециевидный сигнал 12

2.1.4 Пилообразного сигнал 14

2.1.5 Параболический сигнал 15

2.2 Практическая часть 16

3 Анализ 22

3.1 Анализ огибающей спектра 22

3.2 Анализ смоделированного 24

ВВЕДЕНИЕ

Цель работы: изучение спектров простейших периодических сигналов, исследование зависимости формы и параметров спектра от формы и параметров сигнала, получение навыков экспериментального измерения амплитудных спектров сигналов

Оборудование:

1. персональный компьютер для генерации сигналов

2. компьютерная программа «SignalGen»

3. анализатор спектра СК4-56

1. Краткая теория

Периодический сигнал, это такой сигнал S(t), для которого выполняется равенство

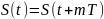(1)

Где T – постоянная величина – период сигнала, m – любое целое число, положительное или отрицательное. Такое определение периодичности предполагает существование процесса на интервале 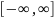, что является идеализацией. В данной работе для разложения сигналов применяется формальная система тригонометрических базисных функций.

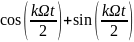(2)

С учетом свойств четности входящих в ряд Фурье функций сигнал можно представить в виде

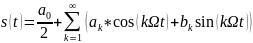(1) (3)

где 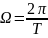, а коэффициенты разложения 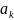и 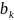определяются по формулам

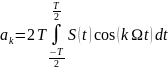(4)

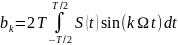(5)

Величина 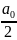называется средним значением или постоянной составляющей сигнала S(t):

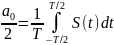(6)

Разложение (3) можно записать в несколько иной форме:

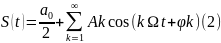(7)

где

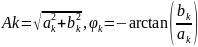(8)

Суммы гармонических составляющих 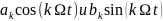в (3) и 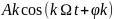в (7), с частотами, кратными основной частоте, определяют переменную составляющую колебания S(t). Совокупность амплитуд 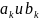гармонических составляющих в (3) является формальным спектром сигнала S(t), а совокупность амплитуд Ак и начальных фаз гармонических составляющих ряда (7), приведенных на рисунке 1, - амплитудным и фазовым спектрами соответственно.

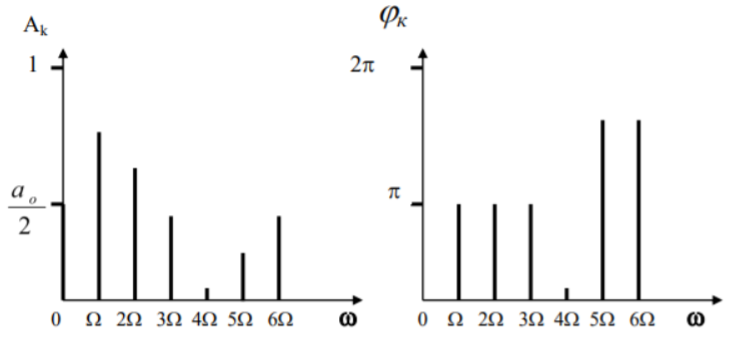
Рисунок 1. Амплитудный 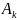и фазовый 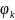спектры сигнала S(t) при разложении (7)

Ряд Фурье может быть записан также в комплексном виде. Известно, что

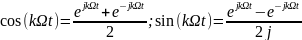(9)

Подставляя эти выражения в (3) и выполняя несложные преобразования, получим 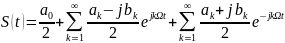(10)

(10)

Обозначим

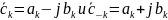(11)

Тогда

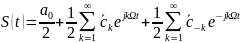(12)

Полагая 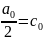и учитывая, что

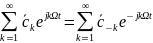(13)

приведем разложение S(t) к окончательному виду

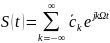(14)

Выражение (14) определяет разложение функции S(t) по системе комплексных экспоненциальных базисных функций. В разложении (14) суммирование членов происходит как с положительными, так и с отрицательными частотами. Отрицательные частоты появляются вследствие формального представления тригонометрических функций в виде совокупности показательных функций с мнимым аргументом. Очевидно, что гармонические колебания с отрицательной частотой, по аналогии с колебаниями, имеющими положительную частоту, можно представить в виде вектора, который вращается на плоскости с постоянной угловой скоростью по часовой стрелке. Комплексная амплитуда 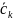спектральной составляющей 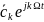разложения (14) представима в виде

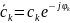(15)

Амплитудный и фазовый спектры сигнала S(t) при разложении (14) определяются совокупностью модулей комплексных амплитуд 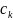и фаз соответственно (рис. 2).

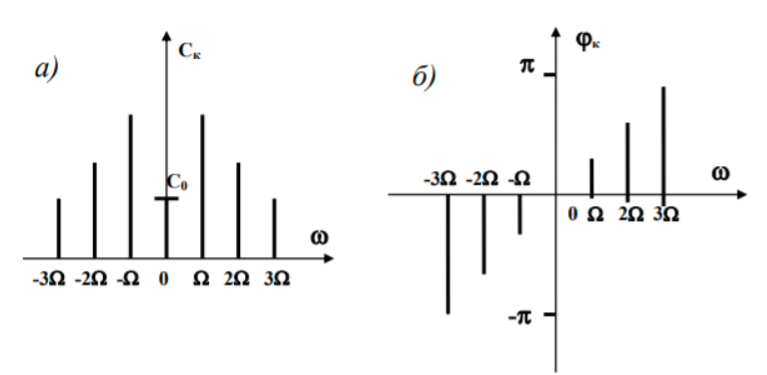
Рисунок 2. Амплитудный спектр а) и фазовый б) спектры сигнала S(t) при разложении (14)

Коэффициенты 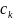(15) разложения (14) связаны с коэффициентами 𝐴𝑘 разложения (7) отношением

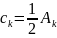(16)

Спектральный анализ упрощается, если на сигнал S(t) наложить дополнительные условия.

Пусть S(t) – четная функция, т.е. S(-t)= S(t) (рис. 3а).

При таком условии коэффициенты разложения S(t) в ряд Фурье (3) принимают вид

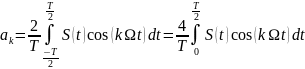(17)

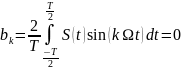(18)

Следовательно, в разложении (3) останутся только члены, содержащие четные базисные функции

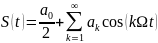(19)

Если S(t) нечетная функция, т.е.

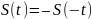
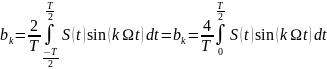(20)

Ряд Фурье в этом случае содержит только члены с нечетными базисными функциями

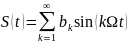(21)

В разложении Фурье общего вида (3) сума (7) является четной функцией времени 𝑆ч (t), а сумма (8) – нечетной 𝑆н(t). Отсюда вытекает, что любую периодическую функцию можно представить как совокупность четного и нечетного слагаемых

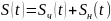(22)

2 Ход работы

2.1 Теоретическая часть

2.1.1 Прямоугольный сигнал

Для начала найдём спектральные составляющие для прямоугольного сигнала

Т.к. сигнал является функцией чётной, то коэффициенты будем искать в виде

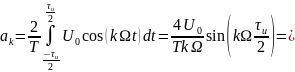
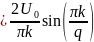
Далее коэффициенты 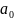будем искать в виде

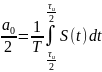
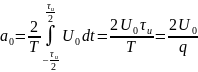
Спектр обращается в нуль при

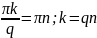
Получим график спектра для всех трёх скважностей:

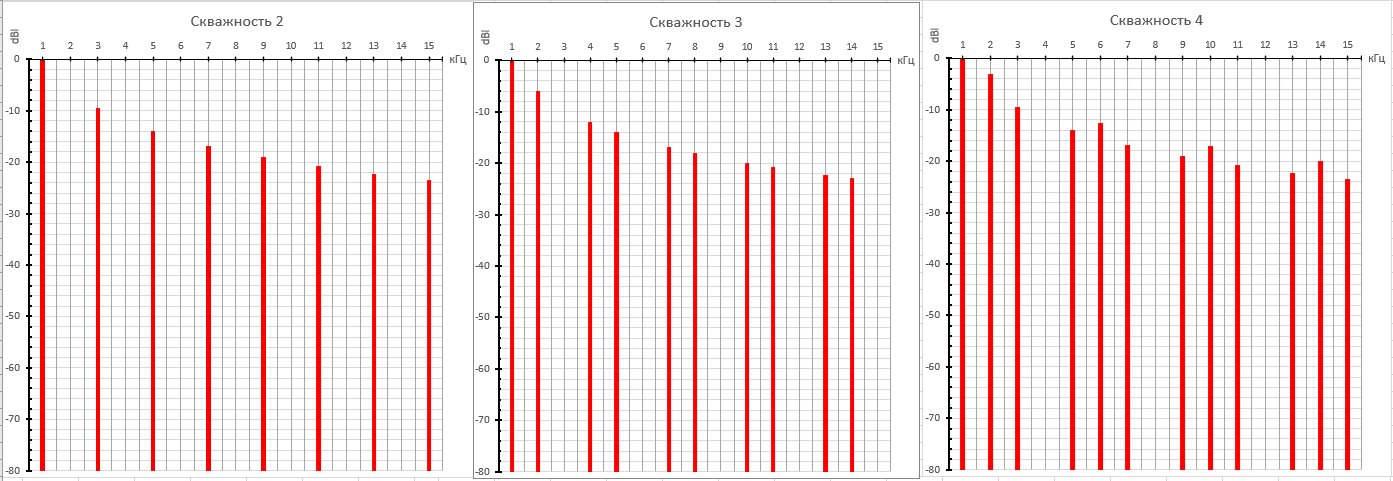
Рисунок 4. Теоретический спектр прямоугольного сигнала

2.1.2 Треугольный сигнал

Теперь найдём спектральные составляющие для треугольного сигнала

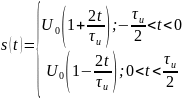
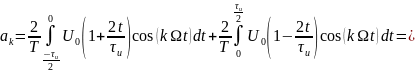
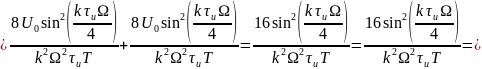
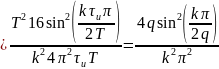
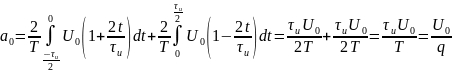
Спектр обращается в нуль при:

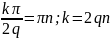
Получим график спектра для всех трёх скважностей:

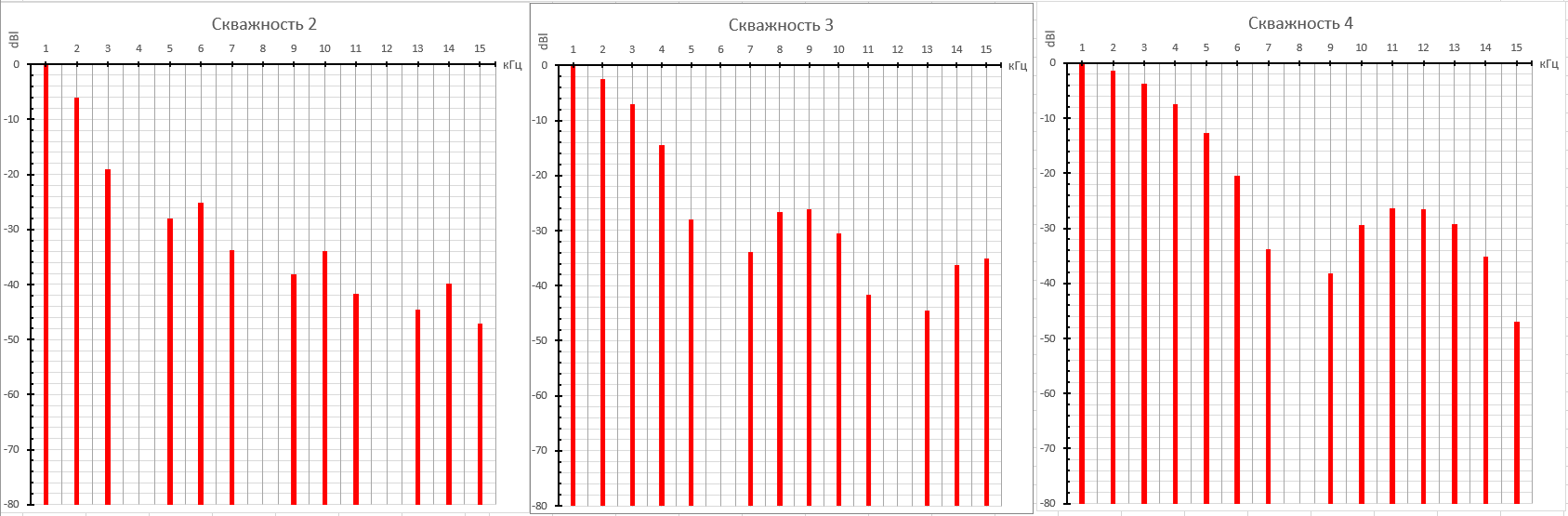
Рисунок 8. Теоретический спектр треугольного сигнала

2.1.3 Трапециевидный сигнал

Теперь найдём спектральные составляющие для трапециевидного сигнала

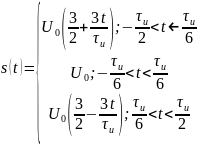
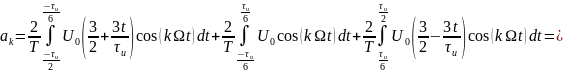
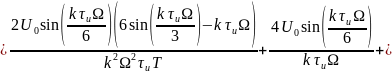
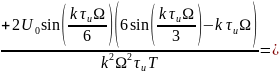
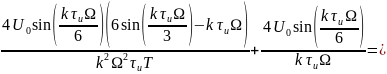
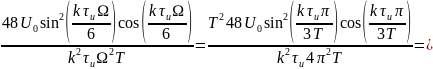
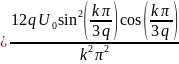
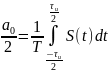
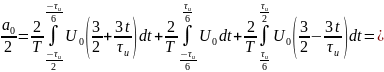
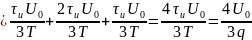
Спектр обращается в нуль при:

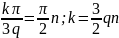
Получим график спектра для всех трёх скважностей:

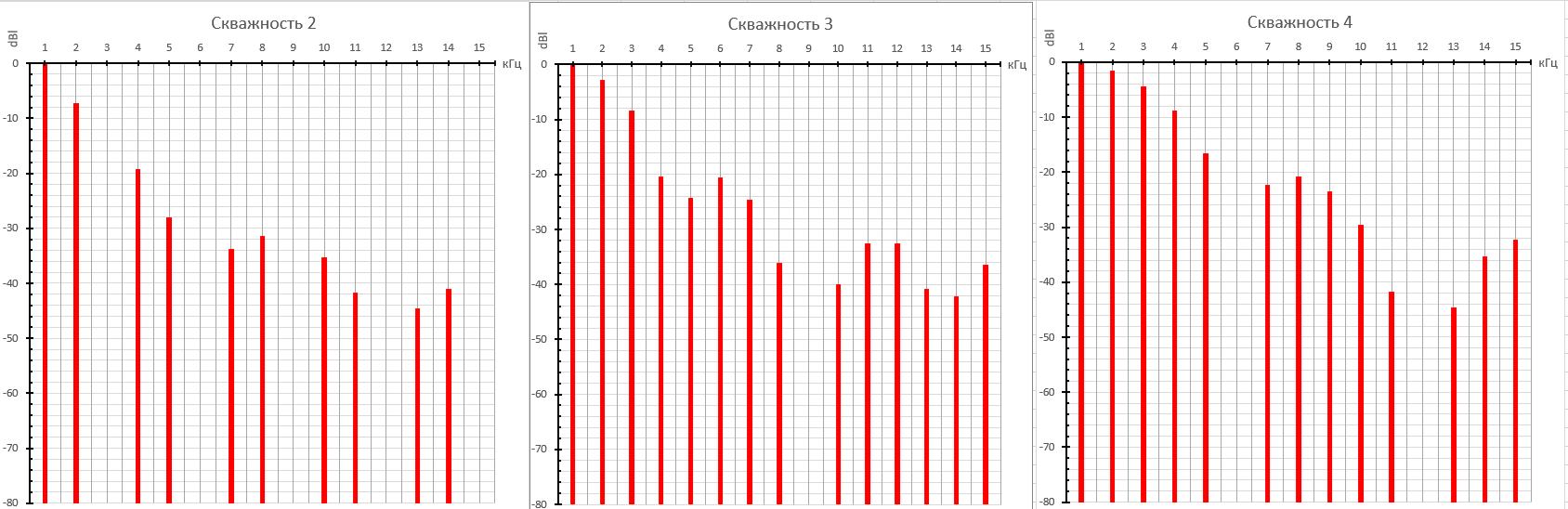
Рисунок 12. теоретический спектр трапециевидного сигнала

2.1.4 Пилообразного сигнал

Теперь найдём спектральные составляющие для пилообразного сигнала

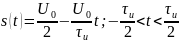
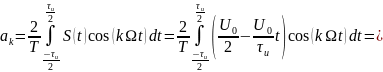
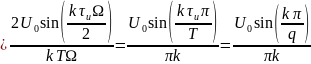
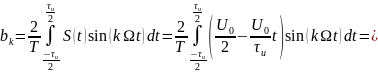
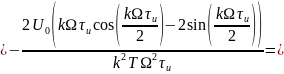
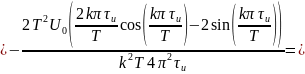
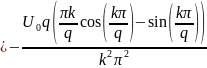
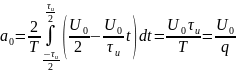
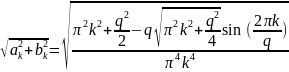
Спектр обращается не обращается в нуль т.к. он стремится к нему. Это видно благодаря другой форме записи формулы, огибающей спектра:

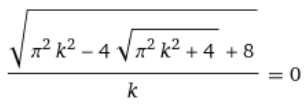
Данное уравнение стремится к нулю.

Получим график спектра для всех трёх скважностей:

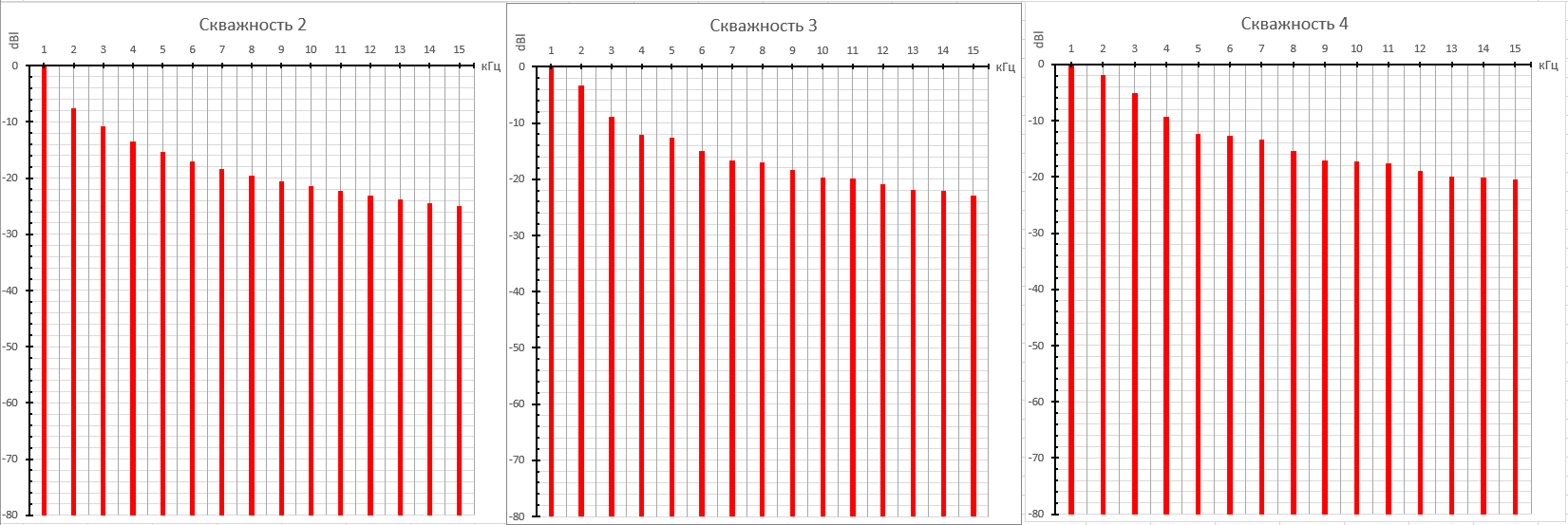
Рисунок 16. Теоретический спектр пилообразного сигнала

2.1.5 Параболический сигнал

Теперь найдём коэффициенты для параболического сигнала

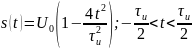
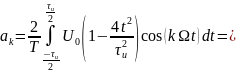
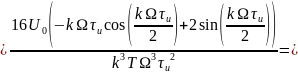
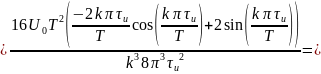
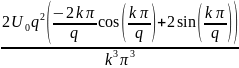
Получим график спектра для всех трёх скважностей:

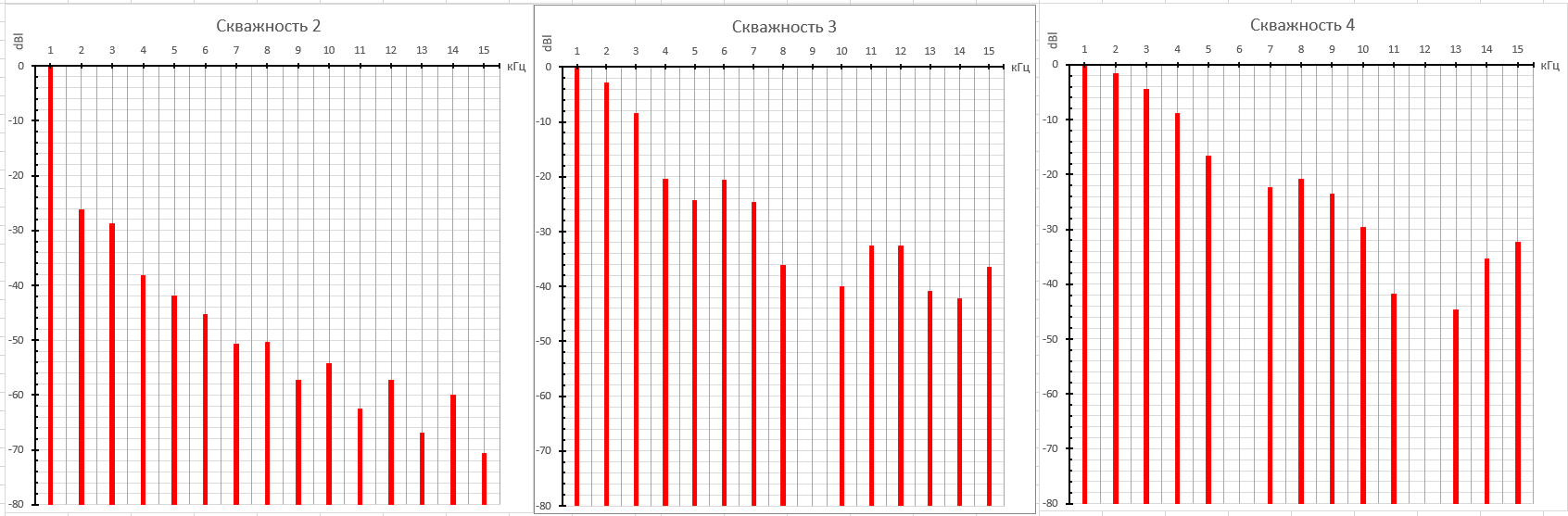
Рисунок 17. Теоретический спектр параболического сигнала

2.2 Практическая часть

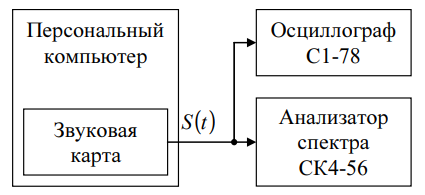
Рисунок 18. Структурная схема лабораторной установки.

1. Собрали установку, согласно структурной схеме, приведённой на рисунке 18, загрузили персональный компьютер, запустили программу «Генератор сигналов специальной формы», включили формирование сигнала звуковой картой персонального компьютера.

2. С помощью анализатора спектра произвели измерения амплитуд спектральных составляющих с порядковыми номерами 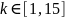при значениях скважности импульсов 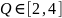, рассчитали погрешности измерений, как указано в техническом описании и инструкции по эксплуатации анализатора спектра. Сравнили результаты с аналитическими зависимостями спектра от формы и параметров сигнала, полученными в теоретической части работы.

Все измерения занесли в таблицы:

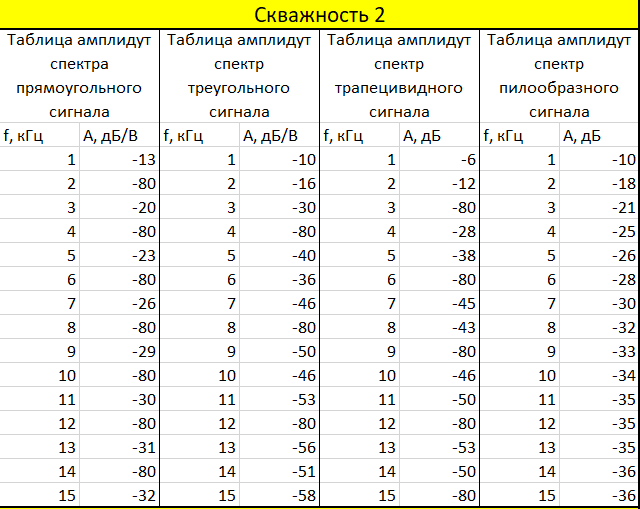
Таблица 1. Амплитудный спектр скважность 2

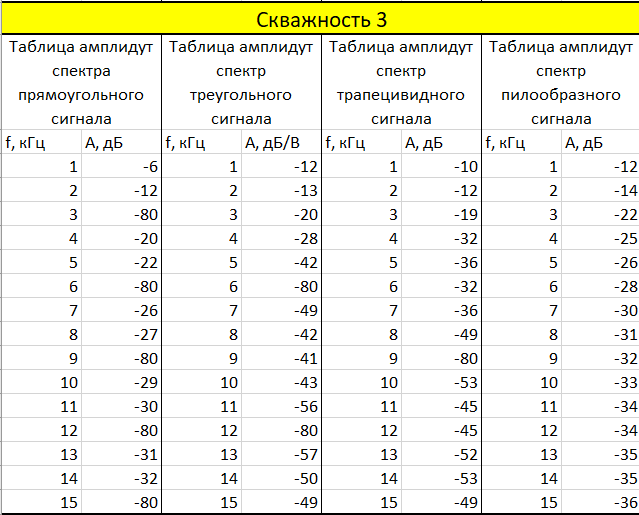
Таблица 2. Амплитудный спектр скважность 3

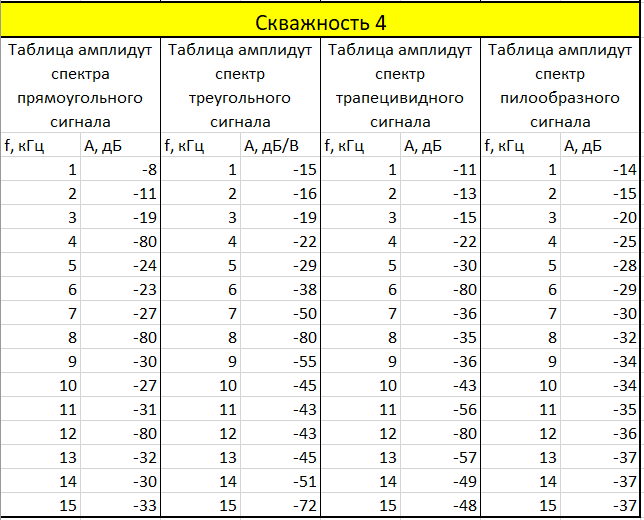
Таблица 3. Амплитудный спектр скважность 4

Так же про нормировали все данные и построили графики спектра:

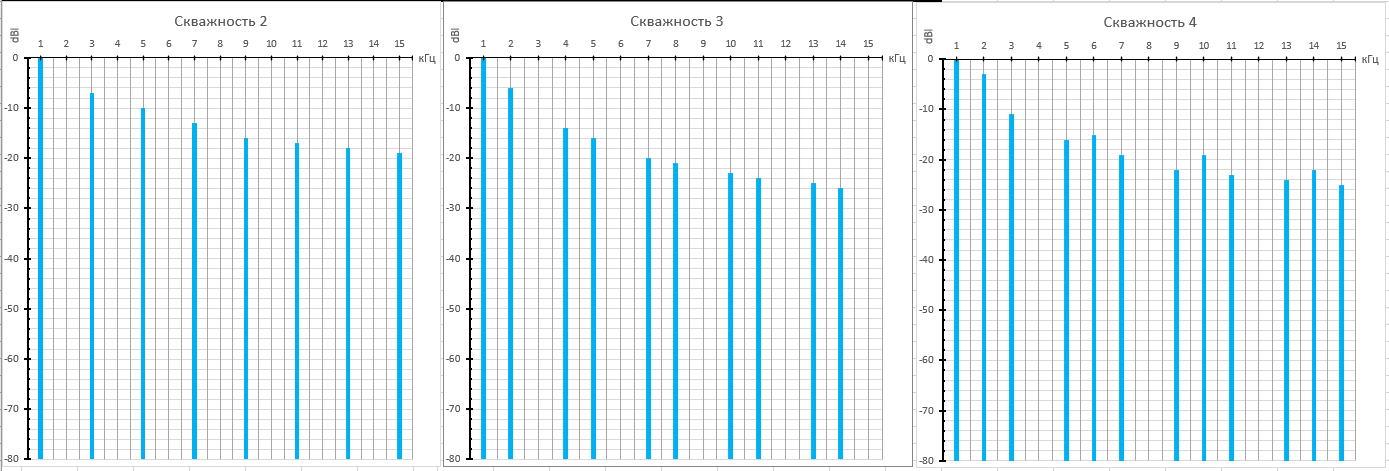
Рисунок 19. Практический спектр прямоугольного сигнала

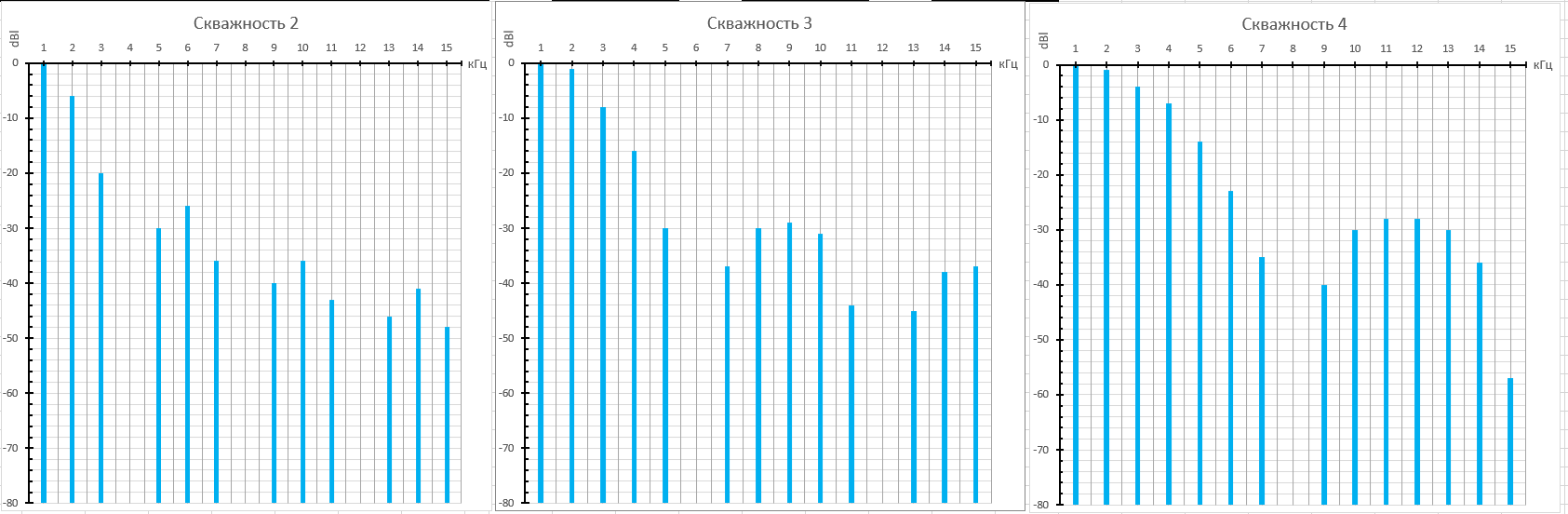
Рисунок 20. Практический спектр треугольного сигнала

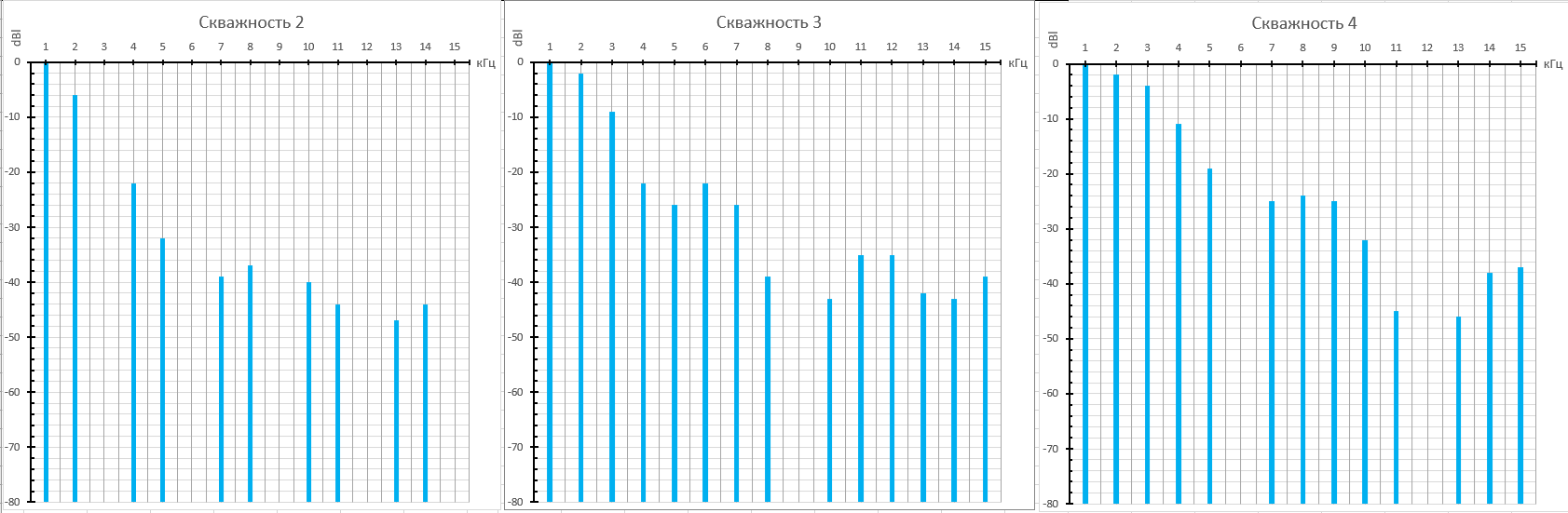
Рисунок 21. Практический спектр трапециевидного сигнала

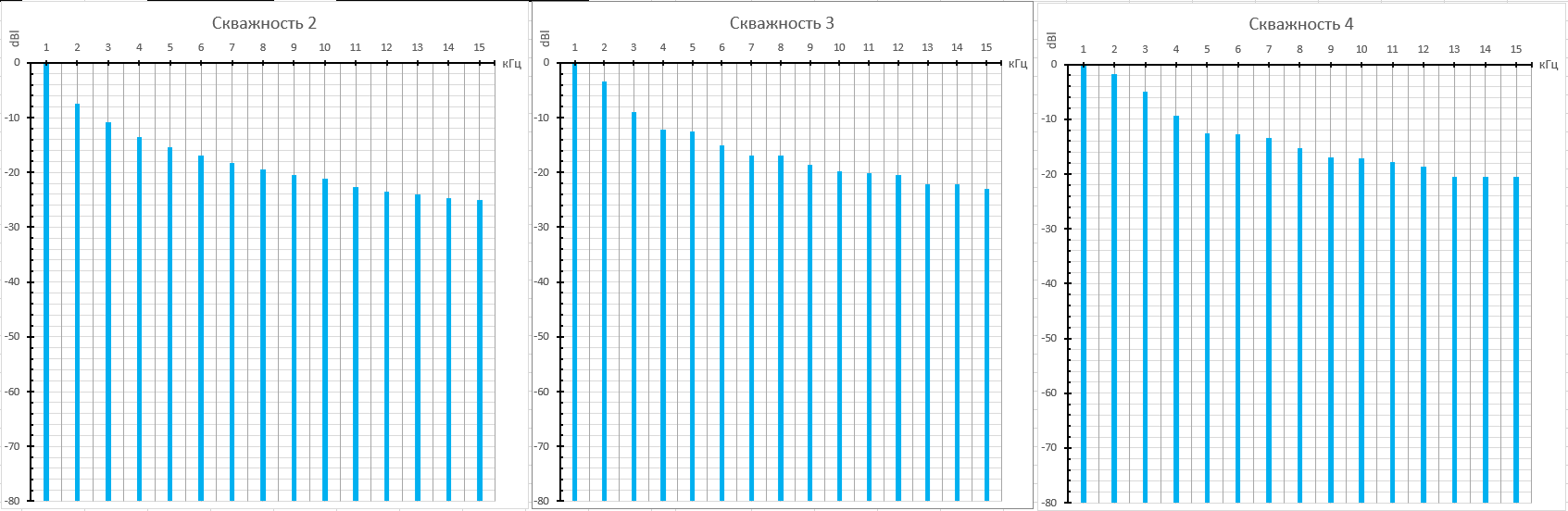
Рисунок 22. Практический спектр пилообразного сигнала

3. По графику спектра в программе «Генератор сигналов специальной формы» выполнили измерения амплитуд спектральных составляющих с порядковыми номерами 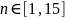при значениях скважности импульсов . Для видов сигнала пилообразного и параболического. Данные занесли в таблицу:

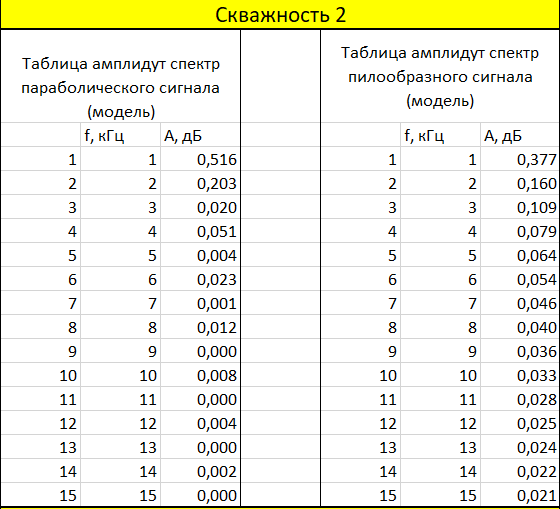
Таблица 5. Амплитудный спектр модели сигнала скважность 2

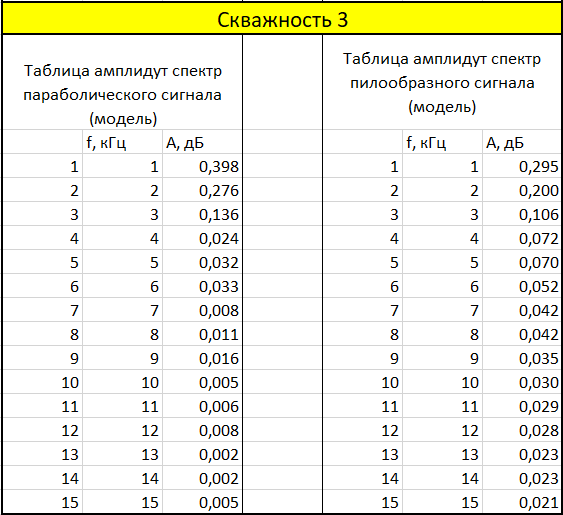
Таблица 6. Амплитудный спектр модели сигнала скважность 3

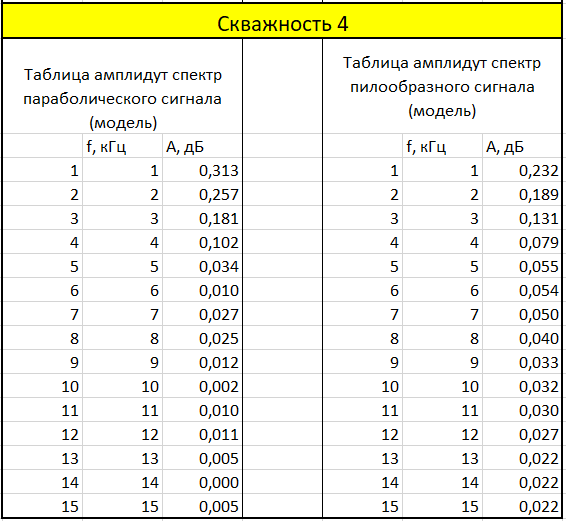
Таблица 7. Амплитудный спектр модели сигнала скважность 4

Далее про нормировали все данные и построили график:

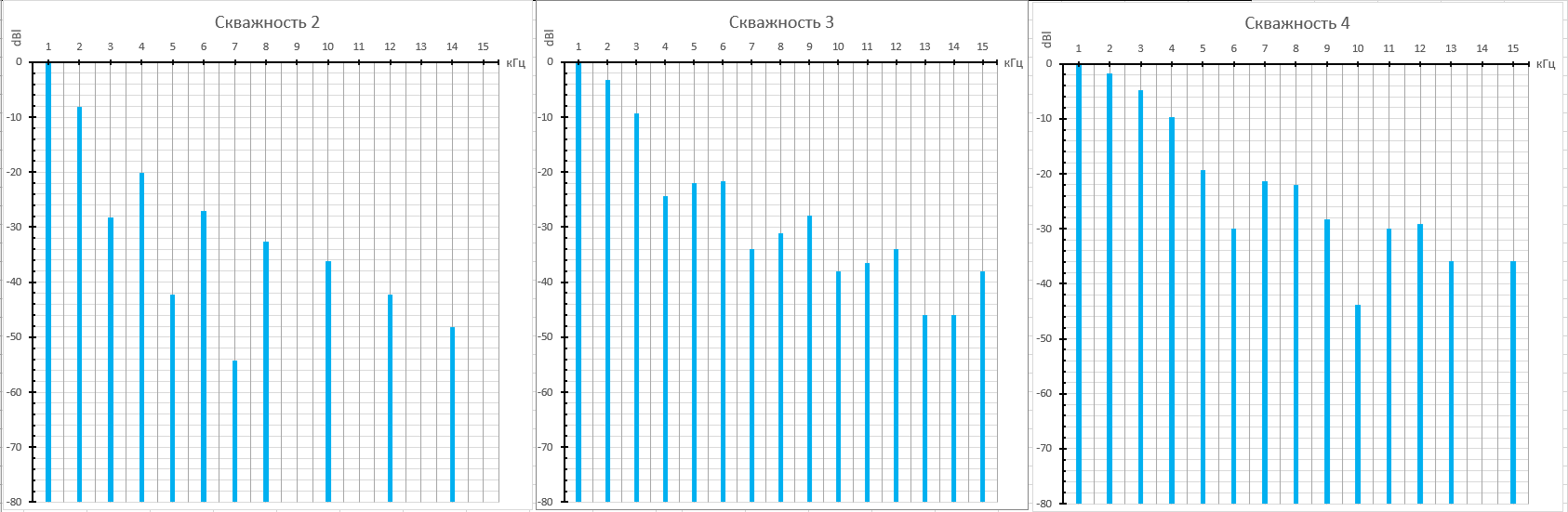
Рисунок 23. Спектр смоделированного параболического сигнала

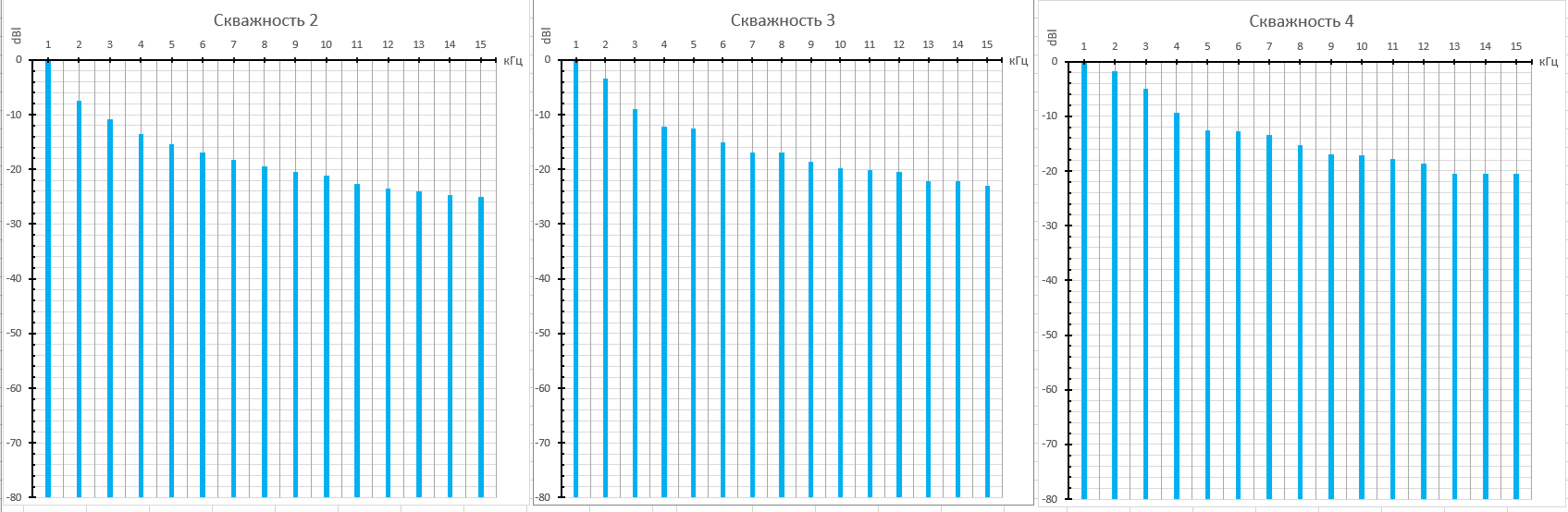
Рисунок 24. Спектр смоделированного пилообразного сигнала