
Билеты Эгзамен / 21-25
.docx21. Задача двух тел. Приведенная масса.
22. Упругое, неупругое столкновение двух частиц. Отражение от стенки. Замедление нейтронов.
23. Изображение процессов столкновения при помощи диаграммы скоростей.
24. Движение тел с переменной массой. Реактивное движение. Уравнение Циолковского, Мещерского.
25. Момент импульса частицы, системы частиц. Момент внутренних, внешних сил.
Билет 18. Задача двух тел. Приведенная масса
Рассмотрим задачу о движении двух взаимодействующих только между собой материальных точек. Вследствие однородности и изотропности пространства потенциальная энергия взаимодействия может зависеть только от расстояния между точками. Функция Лагранжа для данной задачи запишется в форме:
![]()
Рассматриваемая
система материальных точек замкнута.
Поэтому ее импульс сохраняется, и система
отсчета центра инерции является
инерциальной системой отсчета. Задачу
будем решать в системе отсчета центра
инерции. Начало координат поместим в
центр инерции, что дает![]()
Введем
радиус-вектор ![]() ,
направленный от первой материальной
точки ко второй:
,
направленный от первой материальной
точки ко второй:
![]()
С
помощью формул выразим векторы 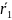 и
и 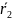 через
вектор
через
вектор 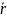 :
:
![]()
![]()
Потенциальная
энергия теперь зависит только от величины
вектора
.
Выражая с помощью формул (4.4)
скорости 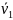 и
и 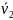 через
вектор
через
вектор 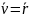 , кинетическую
энергию системы двух материальных точек
можно записать как кинетическую энергию
одной материальной точки массой
, кинетическую
энергию системы двух материальных точек
можно записать как кинетическую энергию
одной материальной точки массой![]()
Выраженная
через радиус-вектор
функция
Лагранжа запишется в форме![]() (4.6)
(4.6)
Функция
Лагранжа (4.6) — это функция Лагранжа
одной материальной точки массы 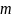 ,
движущейся в потенциальном поле,
зависящем только от расстояния до
начала координат. Такое потенциальное
поле называется Центральным
полем. Сила,
действующая в центральном поле на
материальную точку, направлена по
прямой, соединяющей материальную точку
с центром поля:
,
движущейся в потенциальном поле,
зависящем только от расстояния до
начала координат. Такое потенциальное
поле называется Центральным
полем. Сила,
действующая в центральном поле на
материальную точку, направлена по
прямой, соединяющей материальную точку
с центром поля:![]() (4.7)
(4.7)
Масса , определенная согласно (4.5), называется Приведенной массой. Следовательно, решение задачи двух тел эквивалентно решению задачи о движении в центральном поле материальной точки с массой, равной приведенной массе. После решения задачи о движении материальной точки в центральном поле координаты двух тел можно получить при помощи формул (4.4).
Если
масса одной материальной точки,
например 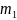 ,
много больше массы другой материальной
точки, то из формул (4.4) и (4.5) получим, что
приближенно
,
много больше массы другой материальной
точки, то из формул (4.4) и (4.5) получим, что
приближенно 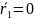 ,
, 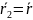 ,
, 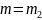 ,
то есть центр инерции системы двух тел
совпадает с более массивным телом,
а приведенная масса равна массе менее
массивного тела. В этом случае задача
двух тел сводится к задаче о движении
одного тела в потенциальном поле,
создаваемом другим телом.
,
то есть центр инерции системы двух тел
совпадает с более массивным телом,
а приведенная масса равна массе менее
массивного тела. В этом случае задача
двух тел сводится к задаче о движении
одного тела в потенциальном поле,
создаваемом другим телом.
Поскольку масса Солнца намного больше массы каждой из планет Солнечной системы, то в первом приближении можно пренебречь взаимодействием планет между собой и движением Солнца вокруг центра инерции Солнечной системы. В этом приближении движение отдельной планеты рассматривается как движение материальной точки в поле тяготения Солнца. Учет взаимодействия планет между собой приводит к задаче многих тел, взаимодействующих между собой. Эта задача не может быть сведена к квадратурам и решается приближенными методами.
Билет 19. Упругое, неупругое столкновение двух частиц. Отражение от стенки. Замедление нейтронов.
Абсолютно
упругим ударом двух тел в нерелятивистском
случае называется такое столкновение,
после которого не остается никаких
деформаций, не изменяется их внутренняя
энергия (шары не нагреваются), а полная
кинетическая энергия до удара равна
полной кинетической энергии тел после
удара.
Рассмотрим центральный
удар абсолютно
упругих шаров. В этом случае скорости
шаров до удара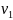 и
и 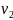 направлены
вдоль прямой, соединяющей их центры.
Эта прямая называется линией центров.
В случае абсолютно упругого удара шары
при столкновении деформируются, и
кинетическая энергия частично переходит
в потенциальную энергию упругих
деформаций. В некоторый момент вся
кинетическая энергия относительного
движения переходят в потенциальную
энергию упруго деформированных шаров.
В этот момент шары аналогичны сжатым
пружинам, стремящимся перейти в
недеформированное состояние. Ввиду
этого начинается обратный переход
энергии упругих деформаций в кинетическую
энергию поступательного движения шаров.
Когда он заканчивается, шары разлетаются
в разные стороны и вновь оказываются
недеформированными. Таким образом,
кинетическая энергия поступательного
движения шаров снова принимает исходное
значение, каким оно было до удара.
Скорости
шаров после столкновения
направлены
вдоль прямой, соединяющей их центры.
Эта прямая называется линией центров.
В случае абсолютно упругого удара шары
при столкновении деформируются, и
кинетическая энергия частично переходит
в потенциальную энергию упругих
деформаций. В некоторый момент вся
кинетическая энергия относительного
движения переходят в потенциальную
энергию упруго деформированных шаров.
В этот момент шары аналогичны сжатым
пружинам, стремящимся перейти в
недеформированное состояние. Ввиду
этого начинается обратный переход
энергии упругих деформаций в кинетическую
энергию поступательного движения шаров.
Когда он заканчивается, шары разлетаются
в разные стороны и вновь оказываются
недеформированными. Таким образом,
кинетическая энергия поступательного
движения шаров снова принимает исходное
значение, каким оно было до удара.
Скорости
шаров после столкновения  и
и 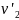 легко
найти из законов сохранения импульса
и потенциальной энергии
легко
найти из законов сохранения импульса
и потенциальной энергии 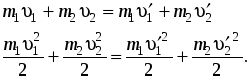 (7.18)
Такая
система должна иметь решение относительно
неизвестных
и
.
Одно решение очевидно
(7.18)
Такая
система должна иметь решение относительно
неизвестных
и
.
Одно решение очевидно
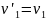 ,
,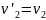 .
Но это решение означает, что столкновения
не было. Это связано с тем, что в законах
столкновения мы рассматриваем два
состояния, разделенных промежутком
времени
.
Но это решение означает, что столкновения
не было. Это связано с тем, что в законах
столкновения мы рассматриваем два
состояния, разделенных промежутком
времени 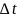 ,
но в законе сохранения не заложено
условие, что это столкновение произошло.
Чтобы получить решение, относящееся к
столкновению, нужно потребовать. чтобы
скорости изменилась. Заметив это,
перепишем (7.18) в виде
,
но в законе сохранения не заложено
условие, что это столкновение произошло.
Чтобы получить решение, относящееся к
столкновению, нужно потребовать. чтобы
скорости изменилась. Заметив это,
перепишем (7.18) в виде![]() Поделив
уравнения почленно друг на друга,
получим
Поделив
уравнения почленно друг на друга,
получим![]() В
результате задача сводится к решению
системы двух линейных уравнений
В
результате задача сводится к решению
системы двух линейных уравнений
![]() Решение
этой системы уравнений имеет следующий
вид
Решение
этой системы уравнений имеет следующий
вид
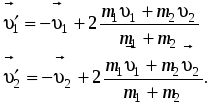 Рассмотрим
несколько частных случаев столкновения
двух шаров.
1.
Пусть два шара перед столкновением
имеют импульсы, равные по величине, но
противоположные по направлению, то
есть
Рассмотрим
несколько частных случаев столкновения
двух шаров.
1.
Пусть два шара перед столкновением
имеют импульсы, равные по величине, но
противоположные по направлению, то
есть ![]() .
Тогда, согласно полученным формулам,
скорости шаров после удара равны
соответственно
.
Тогда, согласно полученным формулам,
скорости шаров после удара равны
соответственно ![]() и
и ![]() и,
следовательно, в результате столкновения
импульсы шаров изменяются на противоположные
по направлению и шары разлетаются с
прежними по величине скоростями.
2.
Пусть один из шаров покоится,
и,
следовательно, в результате столкновения
импульсы шаров изменяются на противоположные
по направлению и шары разлетаются с
прежними по величине скоростями.
2.
Пусть один из шаров покоится, ![]() .
Скорости шаров после столкновения
.
Скорости шаров после столкновения
![]() ,
, ![]() .
Таким
образом, после столкновения оба шара
будут иметь скорости, отличные от нуля,
но их величины
.
Таким
образом, после столкновения оба шара
будут иметь скорости, отличные от нуля,
но их величины ![]() и
и ![]() будут
зависеть от соотношения масс шаров,
участвующих в столкновении.
а) при
будут
зависеть от соотношения масс шаров,
участвующих в столкновении.
а) при ![]() скорость
первого шара уменьшается по величине,
но сохраняет свое направление. Часть
кинетической энергии этого шара
передается второму шару. Кинетическая
энергия, приобретенная вторым
шаром
скорость
первого шара уменьшается по величине,
но сохраняет свое направление. Часть
кинетической энергии этого шара
передается второму шару. Кинетическая
энергия, приобретенная вторым
шаром
![]() .
Очевидно,
переданная второму шару энергия
максимальна, когда
.
Очевидно,
переданная второму шару энергия
максимальна, когда ![]() .
В этом случае первый шар останавливается,
а вся его энергия
.
В этом случае первый шар останавливается,
а вся его энергия ![]() переходит
в кинетическую энергию второго шара
переходит
в кинетическую энергию второго шара ![]() .
Если
.
Если ![]() ,
то переданная энергия
,
то переданная энергия 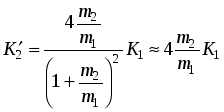 мала.
Импульс второго шара после удара
мала.
Импульс второго шара после удара 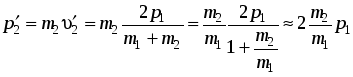 также
мал по сравнению с
также
мал по сравнению с ![]() ,
хотя скорость
мало
отличается от
,
хотя скорость
мало
отличается от ![]() Действительно,
Действительно, ![]() .
b)
При
.
b)
При ![]() направление
движения первого шара изменяется на
противоположное
направление
движения первого шара изменяется на
противоположное ![]() ,
а второй шар начнет двигаться в направлении
движения первого шара до столкновения
,
а второй шар начнет двигаться в направлении
движения первого шара до столкновения ![]() .
При
.
При ![]() от
первого шара второму переходит энергия
от
первого шара второму переходит энергия ![]() ,
то есть малая ее часть. Импульс второго
шара
,
то есть малая ее часть. Импульс второго
шара ![]() ,
а скорость
,
а скорость![]() .
Например,
при ударе шара о стенку можно принять
.
Например,
при ударе шара о стенку можно принять ![]() ,
тогда
,
тогда ![]() ,
а
,
а ![]() ,
и, следовательно, шар отскакивает от
стенки, сохраняя кинетическую энергию
неизменной.
Можно
решить задачу о столкновении в системе
центра масс (Ц - системе). Относительно
лабораторной системы отсчета центр
масс движется со скоростью
,
и, следовательно, шар отскакивает от
стенки, сохраняя кинетическую энергию
неизменной.
Можно
решить задачу о столкновении в системе
центра масс (Ц - системе). Относительно
лабораторной системы отсчета центр
масс движется со скоростью
![]() .
Если
воспользоваться теперь нерелятивистским
законом сложения скоростей, то для
скоростей частиц после столкновения
получим следующие выражения
.
Если
воспользоваться теперь нерелятивистским
законом сложения скоростей, то для
скоростей частиц после столкновения
получим следующие выражения
![]() ,
, ![]() .
Таким
образом в системе центра масс столкновение
приводит просто к изменению знака каждой
скорости.
.
Таким
образом в системе центра масс столкновение
приводит просто к изменению знака каждой
скорости.
Замедление
нейтронов
Особенности
упругого удара имеют многие важные
применения, например, для замедления
нейтронов в ядерном реакторе. Энергия,
которая выделяется в ядерных реакторах
— это энергия деления ядер урана при
столкновении их с нейтронами. Вероятность
захвата нейтрона тем больше, чем меньше
их кинетическая энергия. Для ее уменьшения
в активную зону реактора вводится
графит, масса ядра атома углерода,
который входит в графит, приблизительно
в 12 раз больше массы нейтрона. Поэтому
при каждом центральном столкновении
нейтрона с ядром графита ядру
передается ![]() энергии
нейтрона и процесс замедления идет
быстро.
энергии
нейтрона и процесс замедления идет
быстро.
Абсолютно
неупругий удар
Интересным
примером, где имеет место переход
механической энергии в другие виды
энергии под действием диссипативных
сил, является абсолютно неупругий удар.
Так называется столкновение двух тел,
в результате которого они соединяются
вместе и движутся дальше как одно
тело.
Н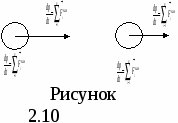 айти
скорость тела можно не вдаваясь в
механизм явления, а используя только
закон сохранения импульса. Рассмотрим
центральный удар.
Пусть
два шара массами
и
айти
скорость тела можно не вдаваясь в
механизм явления, а используя только
закон сохранения импульса. Рассмотрим
центральный удар.
Пусть
два шара массами
и  движутся
со скоростями
и
.
При столкновении образуется тело
массой
движутся
со скоростями
и
.
При столкновении образуется тело
массой 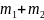 ,
движущееся со скоростью
.
Запишем закон сохранения импульса для
такого удара
,
движущееся со скоростью
.
Запишем закон сохранения импульса для
такого удара ![]() .
В
проекции на ось, совпадающую по направлению
со скоростью движущихся частиц, закон
сохранения импульса запишется следующим
образом
.
В
проекции на ось, совпадающую по направлению
со скоростью движущихся частиц, закон
сохранения импульса запишется следующим
образом
О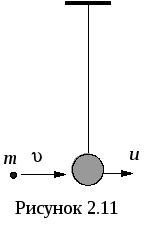 тсюда
скорость движения слипшегося тела после
столкновения
тсюда
скорость движения слипшегося тела после
столкновения![]() Изменение
механической энергии системы для
рассматриваемого случая равно изменению
ее кинетической энергии
Изменение
механической энергии системы для
рассматриваемого случая равно изменению
ее кинетической энергии![]() где
где ![]() -
приведенная масса системы.
Таким
образом, при столкновении двух абсолютно
неупругих шаров происходит потеря
кинетической энергии макроскопического
движения, равная половине произведения
приведенной массы на квадрат относительной
скорости.
Во
время столкновения в системе действуют
диссипативные силы, уменьшающие
кинетическую энергию макроскопического
движения. Поэтому применять закон
сохранения механической энергии к
процессам, происходящим во время удара,
нельзя. Но после того, как удар закончился
и тела соединились, законом сохранения
механической энергии уже можно
пользоваться.
В
качестве примера можно рассмотреть
задачу о баллистическом маятнике. Пусть
на маятник массой
-
приведенная масса системы.
Таким
образом, при столкновении двух абсолютно
неупругих шаров происходит потеря
кинетической энергии макроскопического
движения, равная половине произведения
приведенной массы на квадрат относительной
скорости.
Во
время столкновения в системе действуют
диссипативные силы, уменьшающие
кинетическую энергию макроскопического
движения. Поэтому применять закон
сохранения механической энергии к
процессам, происходящим во время удара,
нельзя. Но после того, как удар закончился
и тела соединились, законом сохранения
механической энергии уже можно
пользоваться.
В
качестве примера можно рассмотреть
задачу о баллистическом маятнике. Пусть
на маятник массой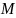 налетает
со скоростью
налетает
со скоростью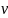 пуля
массой
.
Для простоты расчета будем считать
маятник математическим. Процесс
столкновения происходит настолько
быстро, что за время столкновения,
маятник не успевает отклониться на
заметный угол. В результате удара он
только приходит в движение и задача
заключается в том, чтобы найти скорость
после удара. Во время удара всеми силами,
действующими на маятник, можно пренебречь
по сравнению с силой, с которой на маятник
действует налетающая пуля, то есть
систему маятник-пуля можно считать
замкнутой и использовать закон сохранения
импульса. В проекции на направление
движения пули закон сохранения импульса
выглядит следующим образом
пуля
массой
.
Для простоты расчета будем считать
маятник математическим. Процесс
столкновения происходит настолько
быстро, что за время столкновения,
маятник не успевает отклониться на
заметный угол. В результате удара он
только приходит в движение и задача
заключается в том, чтобы найти скорость
после удара. Во время удара всеми силами,
действующими на маятник, можно пренебречь
по сравнению с силой, с которой на маятник
действует налетающая пуля, то есть
систему маятник-пуля можно считать
замкнутой и использовать закон сохранения
импульса. В проекции на направление
движения пули закон сохранения импульса
выглядит следующим образом![]() ,
где
,
где 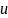 -
скорость системы после удара. После
удара диссипативные силы не действуют,
поэтому можно использовать закон
сохранения механической энергии
-
скорость системы после удара. После
удара диссипативные силы не действуют,
поэтому можно использовать закон
сохранения механической энергии![]() где
где 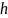 -
высота, на которую поднимется маятник,
-
высота, на которую поднимется маятник,
![]() .
Измерив
,
можно вычислить скорость пули
.
.
Измерив
,
можно вычислить скорость пули
.
Билет 20 . Уравнение движения тела переменной массы
Получим
уравнение движения тела переменной
массы (например, движение ракеты
сопровождается уменьшением ее массы
за счет истечения газов, образующихся
от сгорания топлива).
Пусть
в момент времени t масса
ракеты m,
а ее скорость v;
тогда по истечении времени dt ее
масса уменьшится на dm и
станет равной m–dm,
а скорость увеличится до величины v+dv.
Изменение импульса системы за
время dt будет
равно:
![]() где u -
скорость истечения газов относительно
ракеты. Раскрывая скобки в этом выражении,
получим:
где u -
скорость истечения газов относительно
ракеты. Раскрывая скобки в этом выражении,
получим:
![]() Если на систему действуют внешние силы,
то
Если на систему действуют внешние силы,
то ![]() или
или 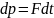 .
Тогда
.
Тогда 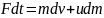 ,
или
,
или![]() (2.12),
где член
(2.12),
где член ![]() называют реактивной
силой
называют реактивной
силой 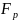 .
Если вектор
.
Если вектор 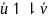 ,
то ракета ускоряется,
,
то ракета ускоряется,
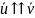 ,
то тормозится.
Таким образом, уравнение
движения тела переменной массы имеет
следующий вид:
,
то тормозится.
Таким образом, уравнение
движения тела переменной массы имеет
следующий вид:
![]() (2.13)называется уравнением
И.В. Мещерского.
Применим
уравнение (2.12) к движению ракеты, на
которую не действуют никакие внешние
силы. Тогда, полагая F =
0 и считая, что ракета движется прямолинейно
(скорость истечения газов постоянна),
получим:
(2.13)называется уравнением
И.В. Мещерского.
Применим
уравнение (2.12) к движению ракеты, на
которую не действуют никакие внешние
силы. Тогда, полагая F =
0 и считая, что ракета движется прямолинейно
(скорость истечения газов постоянна),
получим:
![]() ⟹
⟹![]() или
или![]() где
где 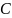 –
постоянная интегрирования, определяемая
из начальных условий. Если в начальный
момент времени
–
постоянная интегрирования, определяемая
из начальных условий. Если в начальный
момент времени 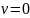 ,
а стартовая масса ракеты составляет
,
а стартовая масса ракеты составляет 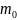 ,
то
,
то 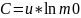 .
Следовательно,
.
Следовательно,
![]() (2.14) формулой
К.Э. Циолковского.
Из выражения (2.14) следуют следующие
практические выводы:
а)
чем больше конечная масса ракеты
,
тем больше должна быть стартовая
масса m0;
б)
чем больше скорость истечения газов
,
тем больше может быть конечная масса
при данной стартовой массе
ракеты.
Уравнения
Мещерского и Циолковского справедливы
для случаев, когда скорости v и u намного
меньше скорости света
(2.14) формулой
К.Э. Циолковского.
Из выражения (2.14) следуют следующие
практические выводы:
а)
чем больше конечная масса ракеты
,
тем больше должна быть стартовая
масса m0;
б)
чем больше скорость истечения газов
,
тем больше может быть конечная масса
при данной стартовой массе
ракеты.
Уравнения
Мещерского и Циолковского справедливы
для случаев, когда скорости v и u намного
меньше скорости света  .
.
Реактивное движение. В настоящем параграфе говорится о медленном движении тел, масса которых меняется за счет потери или приобретения вещества. Уравнения движения тел с переменной массой являются следствиями законов Ньютона. Тем не менее, они представляют большой интерес, главным образом, в связи с ракетной техникой.
Выведем уравнение движения материальной точки с переменной массой на примере движения ракеты.
Принцип действия ракеты очень прост. Ракета с большой скоростью выбрасывает вещество (газы), воздействуя на него с большой силой. Выбрасываемое вещество с той же, но противоположно направленной силой, в свою очередь, действует на ракету и сообщает ей ускорение в противоположном направлении. Если нет внешних сил, то ракета вместе с выброшенным веществом является замкнутой системой. Импульс такой системы не может меняться во времени. На этом положении и основана теория движения ракет.
Несложные
преобразования закона изменения импульса
приводят к уравнению Мещерского:
![]()
Здесь m –
текущая масса ракеты, –
ежесекундный расход массы, 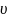 – скорость
газовой струи (т.е.
скорость истечения газов относительно
ракеты),
– скорость
газовой струи (т.е.
скорость истечения газов относительно
ракеты), 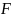 –
внешние силы, действующие на ракету. По
форме это уравнение напоминает второй
закон Ньютона, однако, масса тела m здесь
меняется во времени из-за потери вещества.
К внешней силе
–
внешние силы, действующие на ракету. По
форме это уравнение напоминает второй
закон Ньютона, однако, масса тела m здесь
меняется во времени из-за потери вещества.
К внешней силе 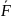 добавляется
дополнительный член
добавляется
дополнительный член 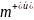 ,
который может быть истолкован
как реактивная
сила.
Применив
уравнение Мещерского к движению ракеты,
на которую не действуют внешние силы,
и проинтегрировав уравнение,
получим формулу Циолковского:
,
который может быть истолкован
как реактивная
сила.
Применив
уравнение Мещерского к движению ракеты,
на которую не действуют внешние силы,
и проинтегрировав уравнение,
получим формулу Циолковского:
![]()
Релятивистское
обобщение этой формулы имеет вид ![]()
|
где c – скорость света. При малых скоростях v оно переходит в формулу Циолковского.
Формула Циолковского позволяет рассчитать запас топлива, необходимый, чтобы сообщить ракете скорость υ. В частности, можно получить, что запас топлива, необходимого для осуществления межзвездного путешествия (с возвращением обратно), должен превышать массу космического корабля в несколько тысяч раз. Но для межзвездных перелетов ракеты на химическом топливе абсолютно непригодны. Расстояния до звезд измеряются световыми годами – от ближайшей звезды свет идет до Земли около 4 лет. Поэтому для достижения даже ближайших звезд нужны космические корабли, скорости которых близки к скорости света c. Если, например, скорость ракеты должна составлять четверть скорости света, то на каждую тонну полезного груза должно приходиться 5∙103327 тонн топлива! (Кстати, при таких скоростях применима только релятивистская формула Циолковского; она еще больше увеличивает необходимое количество топлива). Обычно, когда имеют дело с очень большими величинами, их называют «астрономическими». В данном случае такое сравнение не годится – речь идет о величинах несравненно большего масштаба. Вряд ли имеет смысл говорить о движении столь фантастически гигантского космического корабля относительно Вселенной, имеющей по сравнению с ним ничтожную массу.
Было бы неосторожно на основании вышеизложенного сделать вывод, что звездные миры никогда не будут доступны земным космонавтам. Только отдаленное будущее покажет, возможно это или нет. Для превращения ракеты в звездолет, прежде всего, необходимо повысить скорость струи, приблизив ее к скорости света. Идеальным был бы случай u = c. Так было бы в фотонной ракете, в которой роль газовой струи должен был бы играть световой пучок. Реактивная сила в фотонной ракете осуществлялась бы давлением света. Превращение вещества в излучение постоянно происходит внутри звезд. Этот процесс осуществляется и на Земле (взрывы атомных и водородных бомб). Возможно ли придать ему управляемый характер и использовать в фотонных ракетах – на этот вопрос отвечать сейчас преждевременно.
Билет 21 Момент импульса частицы, системы частиц. Момент внутренних, внешних сил.
Механическая система. Силы внешние и внутренние.
Механической системой материальных точек или тел называется такая их совокупность, в которой положение или движение каждой точки (или тела) зависит от положения и движения всех остальных.
Материальное абсолютно твердое тело мы также будем рассматривать как систему материальных точек, образующих это тело и связанных между собой так, что расстояния между ними не изменяются, все время остаются постоянными.
Классическим примером механической системы является солнечная система, в которой все тела связаны силами взаимного притяжения. Другим примером механической системы может служить любая машина или механизм, в которых все тела связаны шарнирами, стержнями, тросами, ремнями и т.п. (т.е. различными геометрическими связями). В этом случае на тела системы действуют силы взаимного давления или натяжения, передаваемые через связи.
Совокупность тел, между которыми нет никаких сил взаимодействия (например, группа летящих в воздухе самолетов), механическую систему не образует.
В соответствии со сказанным, силы, действующие на точки или тела системы, можно разделить на внешние и внутренние.
Внешними называются силы, действующие на точки системы со стороны точек или тел, не входящих в состав данной системы.
Внутренними называются
силы, действующие на точки системы со
стороны других точек или тел этой же
системы. Будем обозначать внешние силы
символом - ![]() ,
а внутренние -
,
а внутренние - ![]() .
.
Как внешние, так и внутренние силы могут быть в свою очередь или активными, или реакциями связей.
Реакции связей или просто – реакции, это силы которые ограничивают движение точек системы (их координаты, скорость и др.). В статике это были силы заменяющие связи. В динамике для них вводится более общее определение.
Активными или задаваемыми силами называются все остальные силы, все кроме реакций.
Необходимость этой классификации сил выяснится в следующих главах.
