
MSU_Lektsii_Eliseev
.pdfМоделирование систем управления |
|
|
© 2016, В.Л. Елисеев |
|
2) Один конец стержня закреплен, другой свободен: |
|
|
||
u ( 0 , t ) 0 , |
u ( x , t ) |
|
0 |
|
|
||||
x |
||||
|
|
x l |
||
|
|
|
||
На свободном конце = натяжение T равно нулю, так как смещение сечения на краю стержня равно нулю.
3) Оба конца стержня свободны:
u ( x , t ) |
|
0 , |
u ( x , t ) |
0 |
x |
|
x |
||
x 0 |
|
x l |
||
|
|
|
На данном примере видно, что формой математического описания СРП являются дифференциальные уравнения в частных производных (ДУЧП). Рассмотрим общую формулировку и классификацию задач в СРП.
Введем для краткости обозначения:
u |
|
|
u |
, u |
|
|
u |
, u |
|
|
2 u |
, u |
|
|
2 u |
, u |
|
|
2 u |
||
t |
|
x |
|
xx |
|
2 |
tt |
|
2 |
xt |
|
||||||||||
|
|
t |
|
x |
|
|
x |
|
|
t |
|
|
x t |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Тогда в общем виде ДУЧП для одномерной пространственной координаты x может быть записана в виде:
F t , x , u t , u x , u xt , u tt , u xx 0
Уравнение называется линейным относительно старших производных, если можно записать:
a11 u xx 2 a12 u xt a 22 u tt F1 t , x , u t , u x 0
Для заданного уравнения дискриминантом называется D |
a |
2 |
a |
11 |
a |
22 |
. По аналогии с |
|
|
12 |
|
|
|
||
уравнением конического сечения, которое имеет вид |
2 + 2 + 2 = 0 и в |
||||||
зависимости от значения дискриминанта вводится следующая классификация:
D 0 — уравнение эллиптического вида (уравнение Лапласа)
D 0 — уравнение параболического вида (уравнение теплопроводности)
D 0 — уравнение гиперболического вида (волновое уравнение)
Если a 11 a 11 ( u ) , то ДУЧП называется квазилинейным.
Математическая модель объекта теплопроводности
Рассмотрим твердое тело, температура которого в точке (x,y,z) в момент времени t равно u(x,y,z,t). Если различные части тела имеют разную температуру, то тепло будет
распространяться от более теплых частей к более |
холодным. Возьмем какую-нибудь |
|||
поверхность S |
внутри тела и её малый элемент |
S . |
В теории теплопроводности |
|
принимается, |
что количество тепла Q , проходящее |
через S |
за время t |
|
|
81 |
|
|
|

Моделирование систем управления |
|
|
© 2016, В.Л. Елисеев |
||
пропорционально S t и производной u по нормали n к S |
в направлении движения |
||||
тепла, то есть, в направлении, противоположном gradnu: |
|
|
|
||
Q k |
u |
S t k S t grad |
|
u , |
|
|
n |
|
|||
|
n |
|
|
||
|
|
|
|
||
где k>0 – коэффициент внутренней теплопроводности. Будем считать, что теплопроводность в теле обладает свойством изотропности, то есть, зависит только от точки (x,y,z), но не зависит от направления нормали. Обозначим через q тепловой поток, то есть, количество тепла, проходящее через единицу поверхности в единицу времени:
qk u
n
Возьмем внутри тела некоторый объем V, ограниченный гладкой замкнутой поверхностью S и рассмотрим изменение количества тепла в нем за промежуток времени (t1, t2). Очевидно, что количество тепла, которое входит в этот объем можно рассчитать по формуле:
|
|
|
|
|
|
|
|
t 2 |
|
|
|
|
|
|
|
u |
|
|
|
|
Q 1 |
|
dt |
|
k ( x , y , z ) |
dS |
|
||||||||||
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|||
|
|
|
|
|
|
|
|
t1 |
|
|
S |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Применим формулу Остроградского |
div ( F ) dV |
|
( F n ) dS : |
|
||||||||||||||
|
|
|
|
|
|
|
V |
|
|
|
|
|
|
|
S |
|
||
|
|
|
|
|
t 2 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Q 1 |
|
|
dt |
div k grad |
|
( u ) dV |
|
|||||||||
|
|
|
|
|
t1 |
|
|
|
V |
|
|
|
|
|
|
|
|
|
Рассмотрим элемент объема V . |
На изменение его температуры на u |
за время t надо |
||||||||||||||||
потратить количество тепла |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q 2 u ( x , y , z , t t ) u ( x , y , z , t ) ( x , y , z , ) ( x , y , z ) V , |
|
|||||||||||||||||
где ( x , y , z , ), ( x , y , z ) |
- теплоемкость и плотность вещества в данной точке. Таким |
|||||||||||||||||
образом, для изменения температуры объема V необходимо количество тепла: |
||||||||||||||||||
|
Q 2 |
|
u ( x , y , z , t 2 ) u ( x , y , z , t1 ) dV |
|
||||||||||||||
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Поскольку u ( x , y , z , t ) u ( x , y , z , t |
|
) |
t 2 |
u |
dt , то можно записать: |
|
||||||||||||
|
|
|
|
|
|
|||||||||||||
2 |
|
|
1 |
|
|
t |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
t |
1 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
t 2 |
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
Q |
|
|
|
|
dt |
|
dV |
|
|||||
|
|
|
|
|
2 |
|
|
|
|
t |
|
|||||||
|
|
|
|
|
|
|
|
|
t1 |
|
V |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Предположим, в теле имеются источники/поглотители тепла. Обозначим количество тепла выделяемого/поглощаемого в точке в некоторый момент времени через F ( x , y , z , t ) .
82

Моделирование систем управления © 2016, В.Л. Елисеев
Тогда количество тепла, выделяемого/поглощаемого в объеме за промежуток времени будет равно
t 2
Q 3 dt F ( x , y , z , t ) dV
t1 V
Баланс тепла для объема V, очевидно представляет собой Q 2 Q 1 Q 3 , или
t 2 |
|
|
|
u |
|
|
|
t 2 |
|
|
|
|
t 2 |
|
|
|
dt |
|
|
dV |
|
dt |
div k grad |
( u ) dV |
dt F ( x , |
y , z , t ) dV |
|||||||
|
|
|||||||||||||||
t1 |
V |
|
|
t |
|
|
t1 |
V |
|
|
|
t1 |
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
t 2 |
|
|
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
dt |
|
div k grad |
( u ) F ( x , |
|
|
|
|||||||
|
|
|
|
y , z , t ) dV |
0 |
|||||||||||
|
|
t |
||||||||||||||
|
|
t1 |
|
V |
|
|
|
|
|
|
|
|
|
|
||
Так как подынтегральная функция непрерывная, а объем V и промежуток времени (t1, t2) произвольны, то для любой точки (x,y,z) в любой момент времени t справедливо:
|
u |
|
div k grad |
( u ) F ( x , y , z , t ) |
|
t |
|||||
|
|
|
|
или, раскрывая операторы div и grad:
|
u |
|
|
|
u |
|
|
|
u |
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
k |
|
|
|
|
k |
|
|
|
|
|
|
|||||||||
|
t |
|
x |
x |
|
y |
|
y |
|
|
z |
|||
|
|
|
|
|
|
|||||||||
u
F ( x , y , z , t )
z
Типы граничных условий:
1-го рода (Дирихле). Искомая функция задана на границе области:
u 1 ( x ) |
x |
2-го рода (Неймана). На границе области задана производная искомой функции по нормали к границе:
u |
2 ( x ) |
x |
|
n |
|||
|
|
3-го рода (Робена или смешанная). Происходит конвективный теплообмен с внешней средой на границе:
|
u |
u 3 ( x ) |
|
|
|
||
|
|
|
|
|
n |
||
|
x |
||
|
|
|
x |
где - коэффициент теплообмена, |
u - температура поверхности тела в точке, 3 ( x ) - |
||
температура окружающей среды в точке.
Существуют и более сложные граничные условия.
83
Моделирование систем управления |
© 2016, В.Л. Елисеев |
Лекция 14. Метод конечных разностей
Метод конечных разностей (МКР) для моделирования объектов и систем с распределенными параметрами. Основные понятия МКР: разностная сетка, сеточная функция, шаблон, аппроксимация. Примеры аппроксимации простейших дифференциальных операторов, погрешность аппроксимации.
Разностные схемы
Сравнивая задачи по решению ОДУ и УЧП, следует отметить, что первая значительно проще второй. Для некоторых видов ОДУ существует аналитическое решение. Остальные, решаемые численными методами, группируются в небольшое количество классов задач, для каждого из которых есть проработанная теоретическая база и алгоритмы решения. Поэтому часто исследователь, сталкиваясь с задачей решения ОДУ, не выбирает и анализирует метод решения, а просто пользуется стандартной программой.
В случае УЧП очень мало задач имеет решение в явном виде, а число принципиально различных постановок задач существенно больше, чем для ОДУ. Теория численных методов для решения УЧП дробится на большое число направлений. Огромное влияние на развитие этой области вычислительной математики оказало появление и всё более широкое использование ЭВМ. В частности, метод конечных элементов для расчетов на прочность с использованием ЭВМ применялся Аргисом уже в 1944 году.
С тех пор были разработаны алгоритмы для решения подавляющего большинства краевых задач уравнений параболического типа, причем как одномерных, так и многомерных. В то же время, в отличие от ОДУ, далеко не все алгоритмы обоснованы с точки зрения доказательства сходимости и оценки погрешности. Более того, для многих важных прикладных задач даже не доказано существование решения. По этой причине, численное решение УЧП представляет собой полуэмпирическую область, где широко используется метод аналогии, достоверность полученного решения требует доказательств или, хотя бы, некоторого нестрогого обоснования, а анализ численного решения приводит продвижению теории.
Семейство методов, широко используемое для решения наиболее актуальных задач, описываемых УЧП, называется сеточными методами или разностными схемами. Название обусловлено тем, что решение ищется не в непрерывном пространстве переменных исходного УЧП, а в некоторых дискретных точках.
Разностная сетка – это совокупность элементов дискретного пространства.
Каждый отдельный элемент этого пространства называется узлом разностной сетки.
Для того, чтобы решить дифференциальное уравнение разностной схемой необходимо совершить два шага:
Заменить область непрерывного изменения аргументов областью дискретного изменения.
Заменить дифференциальный оператор некоторым разностным оператором, а также сформулировать разностный аналог краевых условий и начальных данных.
84

Моделирование систем управления |
© 2016, В.Л. Елисеев |
Метод конечных разностей
Введем необходимые определения и обозначения. Пусть УЧП имеет общий вид:
|
|
|
|
F t , x , u t , u x , 0 |
|
|
|
|
|||
Надо найти решение в полуполосе 0 |
x |
1 , |
0 t |
|
|
|
|
||||
Зададим некоторые значения h , |
0 |
– это шаги сетки по x |
и t соответственно, причем |
||||||||
1 / h M |
– целое число. |
Точки |
( mh , n ) |
назовем узлами |
сетки |
( m , n ) . |
Пусть u n |
– |
|||
|
|
|
|
|
|
|
|
|
|
m |
|
приближение к значениям u ( mh , n ) |
[ u ] h . |
Обозначим u h |
функцию, определенную на |
||||||||
сетке со значениями в узлах u ( mh , n ) |
. Поскольку на значение шага по времени |
не |
|||||||||
накладывается |
никаких |
ограничений |
кроме положительности, |
обычно |
выбирают |
||||||
/ h |
const |
. Поэтому используется более краткое обозначение |
u h вместо u h и [ u ] h |
||||||||
вместо [ u ] h .
В данном случае разностная сетка задана с регулярным шагом, однако это необязательно.
Функции u ( x , t ) |
непрерывного |
аргумента |
являются |
элементами |
некоторого |
|||||
функционального пространства |
H 0 . |
В свою очередь, множество сеточных функций u h |
||||||||
образуют пространство H h . |
Таким |
образом, |
используя |
метод |
сеток, |
мы заменяет |
||||
пространство H 0 пространством H h . |
|
|
|
|
|
|
|
|||
Говорят, что сеточная функция u h |
сходится к решению задачи УЧП, |
если |
|
|||||||
|
|
u h |
[ u ] h |
|
0 при h 0 |
|
|
|
||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
H h |
|
|
|
|
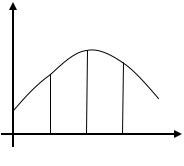
Рассмотрим аппроксимацию дифференциального оператора на разностной сетке. Она производится с помощью так называемого шаблона – линейной комбинации значений сеточной функции u h на некотором множестве узлов сетки.
x
ξ T(x)
Рис.1: Пример шаблона.
Пусть Lu – линейный дифференциальный оператор на функции u. Тогда, заменяя производные в Lu на разностные соотношения, получим разностное выражение L h u h , являющееся линейной комбинацией значений сеточной функции u h :
L h u h x |
|
A h ( x , ) u h ( ) |
T ( x )
85
Моделирование систем управления © 2016, В.Л. Елисеев
где A h ( x , ) – коэффициенты шаблона в узле x разностной сетки, T ( x ) – множество узлов шаблона для узла x.
Приближенная замена L на L h называется аппроксимацией дифференциального оператора разностным.
Количество узлов, входящих в T ( x ) , определяет ранг шаблона. Например, шаблон, состоящий из 3-х точек, называется трехточечным шаблоном.
xm -1 xm xm +1
Рис.2: Значения функции u в окрестности точки xm .
Рассмотрим разностные аппроксимации простейших дифференциальных операторов.
Частная производная первого порядка Lu
следующих выражений:
правая разностная производная:
левая разностная производная: L h u
|
u |
может быть аппроксимирована любым из |
||||||
|
|
|||||||
|
|
x |
|
|
|
|
||
|
|
|
u ( x h ) u ( x ) |
u x |
||||
|
|
|
|
h |
|
|||
|
|
|
|
|
|
|
|
|
|
u ( x ) u ( x h ) |
u |
|
|
||||
|
||||||||
|
|
|
h |
x |
||||
|
|
|
|
|
|
|
|
|
В обоих случаях используется двухточечный шаблон. Кроме того, в качестве разностной аппроксимации производной первого порядка можно взять линейную комбинацию выражений для левой и правой производных:
|
|
|
|
|
|
L( ) |
u |
|
(1 ) u |
|
|
|
|
|
||
|
|
|
|
|
|
h |
|
|
|
x |
|
x |
|
|
|
|
где |
– любое вещественное число. В частности, при |
0 .5 |
получаем так называемую |
|||||||||||||
центральную (двухстороннюю) разностную производную: |
|
|
|
|||||||||||||
|
Lo |
u |
1 |
u |
|
u |
|
|
u ( x h ) u ( x h ) |
u |
|
|||||
|
|
|
|
|
|
|||||||||||
|
|
x |
x |
|||||||||||||
|
h |
2 |
|
|
|
|
|
2 h |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|||
Таким образом, для оценки простейшего дифференциального оператора можно написать бесчисленное множество разностных выражений. Возникает вопрос: какова ошибка аппроксимации при использовании того или иного выражения и как ведет себя разность
( x ) L h u h ( x ) Lu ( x ) в точке x при h 0 ?
86

Моделирование систем управления |
© 2016, В.Л. Елисеев |
Разложим u ( x h ) по формуле Тейлора в окрестности точки x:
u ( x h ) u ( x ) h u ( x ) h 2 u ( x ) O ( h 3 ) 2
Подставим это разложение в формулы для разностных выражений оператора первой производной:
u |
|
|
|
u ( x h ) u ( x ) |
u ( x ) |
h |
u ( x ) O ( h 2 ) |
|
|
|
|
|
|
|||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
h |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
u |
|
|
u ( x ) u ( x h ) |
u ( x ) |
h |
u ( x ) O ( h 2 ) |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
x |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
h |
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
u |
|
u ( x h ) u ( x h ) |
u ( x ) O ( h 2 ) |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
||||||||||||||||
|
x |
|
|
|
2 h |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Отсюда видно, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
u x u ( x ) O ( h ) , |
|
|
u |
|
u ( x ) O ( h ) |
u u ( x ) O ( h 2 ) |
|
||||||||||
|
|
|
|
|
|
|
x |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
Пусть U – класс достаточно гладких функций |
u U , заданных в окрестности T ( x ) |
точки |
||||||||||||||||||||
x, |
содержащей при h h 0 |
|
шаблон разностного оператора |
L h . |
Будем говорить, что L h |
|||||||||||||||||
аппроксимирует дифференциальный оператор L с порядком n 0 |
в точке x, если |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
( x ) L h u ( x ) Lu ( x ) O ( h n ) |
|
|
|
|
||||||
Таким образом, левая и правая производные аппроксимируют Lu |
u с первым порядком, |
|||||||||||||||||||||
а центральная разностная производная – со вторым порядком. |
|
|
|
|||||||||||||||||||
Для разностной аппроксимации частной производной второго порядка Lu u |
2 u |
надо |
||||||||||||||||||||
x 2 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
взять три точки: ( x h , x , x h ) , то есть, взять трехточечный шаблон: |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
L h u |
u ( x h ) 2 u ( x ) u ( x h ) |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Правая разностная производная в точке x совпадает с левой разностной производной в точке x h , то есть, u x ( x ) u x ( x h ) , поэтому:
|
u x ( x ) u |
|
( x ) |
|
1 |
u |
|
|
|
( x ) u |
|
|
L h u |
x |
|
|
( x h ) u |
|
|
x ( x ) |
|||||
|
|
|
|
|
|
|
||||||
h |
|
h |
x |
x |
x |
|||||||
|
|
|
|
|
|
|
|
|
|
|||
Раскладывая функцию u ( x ) в |
ряд |
Тейлора, нетрудно показать, что порядок |
||||||||||
аппроксимации равен двум: |
|
|
|
|
|
|
|
|
|
|
||
87

Моделирование систем управления |
|
|
|
|
|
|
|
|
|
|
|
© 2016, В.Л. Елисеев |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
u |
|
|
u |
h 2 |
|
u ( 4 ) O ( h 4 ) |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
x x |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
|
|
u |
O ( h 2 ) |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x x |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Для аппроксимации производной четвертого порядка Lu u ( 4 ) |
|
4 u |
следует использовать |
||||||||||||||||||||||
x 4 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
пятиточечный шаблон ( x 2 h , x h , x , x h , x 2 h ) . |
|
|
|
||||||||||||||||||||||
Определим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
u |
|
x ( x h ) 2 u |
|
x ( x ) u |
|
x ( x h ) |
|
|
|
|
|
|||||||||
L h u u |
|
|
|
x ( x ) |
x |
x |
x |
|
|
|
|
|
|||||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
x |
x |
|
|
h |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
u ( x 2 h ) 4 u ( x h ) 6 u ( x ) 4 u ( x h ) u ( x 2 h ) h 4
2
Точность аппроксимации – второго порядка: u x x x x u ( 4 ) h u ( 6 ) O ( h 4 )
6
Разложение погрешности аппроксимации по степеням h можно использовать для повышения порядка аппроксимации. Имеем
u |
|
|
u |
h 2 |
u ( 4 ) |
O ( h 4 ) |
|
h 2 |
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x x |
|
|
x x x x |
||||||||||
|
12 |
|
|
12 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
||||
Отсюда следует, что оператор
O ( h 4 ) |
h 2 |
u |
|
x |
|
x |
|
h 4 |
u ( 6 ) O ( h 6 ) |
|
|
||||||||
|
x |
x |
|||||||
12 |
|
|
|
|
|
72 |
|
||
L u |
u |
|
|
|
h 2 |
u |
|
|
|
|
аппроксимирует L u |
|
u |
с четвертым |
|
|
|
|
|
|
|
||||||||
h |
|
x x |
12 |
|
x x x x |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
порядком. Таким же образом можно продолжать и дальше и путем использования всё большего количества точек в шаблоне получать всё более высокий порядок аппроксимации.
88
Моделирование систем управления |
© 2016, В.Л. Елисеев |
Лекция 15. Явный и неявный разностные операторы
Аппроксимация одномерного параболического оператора по схеме с весами. Явный и неявный аппроксимирующий оператор, явная и неявная разностные схемы. Разностная схема повышенного порядка точности.
Аппроксимация одномерного параболического оператора
|
Lu |
u |
|
2 u |
, u u ( x , t ) |
|
|
|
|
|
|
|
|
|
|||
|
|
t |
|
x 2 |
|
|
|
|
Пусть ( x , t ) – фиксированная точка на плоскости и h , |
0 – это шаги сетки по x и t |
|||||||
соответственно. Разностная |
аппроксимация L h для |
|
L требует определить шаблон. |
|||||
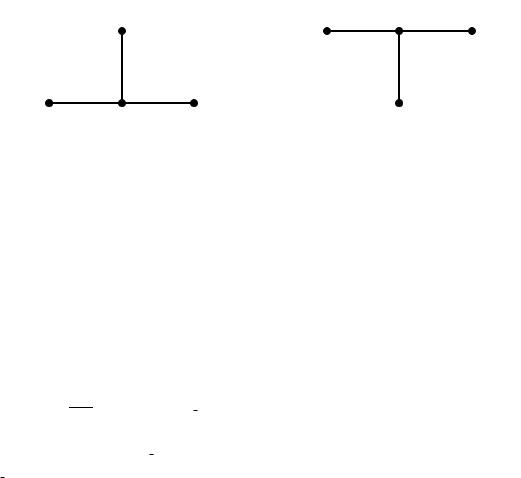
Например, такой как на рис.1а. |
|
|
|
|
|
|
|
|
(x,t+ ) |
|
|
|
|
(x-h,t+ ) |
(x,t+ ) |
(x+h,t+ ) |
|
(x-h,t) |
(x,t) |
(x+h,t) |
(x,t) |
|
a) |
|
б) |
Рис.1: Простейшие шаблоны аппроксимации параболического оператора.
В этих обозначениях разностный оператор определяется выражением:
( 0 ) |
|
u t |
u |
|
|
|
u ( x , t ) u ( x , t ) |
|
u ( x h , t ) 2 u ( x , t ) u ( x h , t ) |
L h |
u |
|
x |
|
|
||||
|
|
|
|||||||
x |
|
h 2 |
Введем обозначения для сокращения записи:
u u ( x , t ) , |
̂ = (, + ), |
u u ( x , t ) |
|
|
|
Тогда = ̂− и L(h0 ) u u t u x x
Для вычисления L(h0 ) u x x берется на нижнем слое, то есть, в момент времени t. Если взять u x x в верхнем слое (рис.1б), то есть, в момент времени t , то оператор будет таким:
(1) = − ̂̅
Взяв линейную комбинацию обоих операторов с параметром , получим семейство разностных операторов, порождающих разностные схемы с весами:
( ) = − (̂̅ + (1 − ) ̅),
89

Моделирование систем управления |
© 2016, В.Л. Елисеев |
определенных при 0 , 1 на шеститочечном шаблоне (рис.2).
(x-h,t+ ) (x,t+ ) (x+h,t+ )
(x-h,t) (x,t) (x+h,t)
Рис.2: Шеститочечный шаблон для аппроксимации параболического оператора.
Точность аппроксимации представленных разностных операторов описывается следующими выражениями (причем 1 / 2 ):
( 0 ) L(h0 ) u Lu ( x , t ) O ( h 2 )
( 1 ) L(h1 ) u Lu ( x , t ) O ( h 2 )
( 0 .5 ) L(h0 .5 ) u Lu ( x , t / 2 ) O ( h 2 2 )
Таким образом, линейная комбинация простейших операторов дает повышенный порядок точности по .
Явные и неявные разностные схемы
Рассмотрим решение УЧП параболического типа
u |
|
2 u |
f ( x , t ) |
|
|
|
|||
t |
x 2 |
|||
|
|
в области Q T [ 0 , X ] [ 0 , T ] с начальными и краевыми условиями:
|
|
|
|
|
|
|
u ( x ,0 ) u 0 ( x ) , |
|
|
|
u ( 0 , t ) 1 ( t ) , |
|
u ( X , t ) 2 ( t ) |
|
|||||
Будем |
считать, |
что |
функции |
f , 1 , 2 , u 0 |
таковы, |
что существует |
достаточно |
гладкое |
|||||||||||
решение изложенной задачи. |
|
|
|
|
|
|
|
|
|
||||||||||
Введем прямоугольную |
сетку: |
Q h |
( mh , n ) : 0 m |
M ,0 n N , |
причем h |
X / M , |
|||||||||||||
|
T / N . |
Обозначим |
u h ( mh , n ) |
u n . |
Используя выведенные ранее выражения для |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
аппроксимации параболического оператора L( 0 ) и |
L( 1 ) |
получим два варианта разностной |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
h |
|
|
|
схемы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
( 0 ) |
: |
u n 1 |
u n |
|
u n |
2 u n |
u n |
|
|
|
n |
|
|
|
|
|
||
L |
|
m |
m |
|
m 1 |
|
m |
m 1 |
|
f |
|
|
|
|
|
|
|||
h |
|
|
|
|
h 2 |
|
m |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
90 |
|
|
|
|
