МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ

РОССИЙСКОЙ ФЕДЕРАЦИИ

НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ «МЭИ»

Кафедра управления и интеллектуальных технологий

Типовой расчет по дисциплине

«ТЕОРИЯ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ»

АНАЛИЗ НЕЛИНЕЙНЫХ СИСТЕМ

АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

Вариант 11

Группа: А-01-20

Выполнил: Дашин И.Н.

Проверила: Сидорова Е.Ю.

Москва 2023

1. Задание на выполнение расчёта

Исходными данными для исследования нелинейной системы являются структурная схема системы с заданными параметрами звеньев и характеристика нелинейного элемента.

Рис.1. Исходная структурная схема нелинейной системы.

Рис. 2. Нелинейный элемент релейного типа (двухпозиционное реле с гистерезисом)

В рамках настоящей работы исследуется система при отсутствии входного воздействия, т.е. .

Передаточные функции исходной системы заданы следующего вида:

; (1.1)

; (1.2)

; (1.3)

z = – характеристика нелинейного элемента релейного типа

Параметры системы и нелинейного элемента:

№	a	b				Тип НЭ	c	h	B
11	1	0.64	3	5	0.2	3	5	8	5

h выбираем из условия h > c: берем из ближайшего по номеру варианта задания с нелинейным элементом вида 4, при котором соблюдается h> c=5. В данном случае ближайший подходящий вариант 4 с h=8.

2. Выполнение расчёта

2.1. Структурные преобразования исходной схемы (рис. 1.)

Объединим передаточные звенья в звено , так как они соединены последовательно, перемножим их передаточные функции:

(2.1)

Ветвь со звеном и единичную обратную связь объединим в эквивалентное звено в соответствии с правилом параллельного соединения:

(2.2)

В результате получим такую структурную схему:

Рис. 3. Приведённая структура схема нелинейной системы

В соответствии с (2.1) и (2.2) запишем связь между переменными в операторной форме:

(2.3)

(2.4)

Перейдём от операторной формы записи дифференциальных уравнений (2.1) и (2.2) к естественной форме с независимым аргументом t.

Подставляя в (2.3) и (2.4) заданные значения параметров и переходя от изображений к оригиналам, получим дифференциальные уравнения следующего вида:

(2.5)

(2.6)

Уравнения (2.5) и (2.6) и уравнение нелинейного элемента:

(2.7)

полностью описывают динамику системы.

Подставим выражение (2.7) для 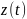и (2.6) для в (2.5):

(2.8)

В результате получаются два типа дифференциальных уравнений с одинаковыми левыми частями и отличающихся значениями постоянных функций в правой части (75; -75). Отсюда следует, что на фазовой плоскости будут иметь место траектории двух типов. Неравенства указывают, в какой области фазовой плоскости справедливы решения (интегральные кривые) того или иного уравнения.

В качестве координат фазовой плоскости примем переменные Тогда система (2.8) представиться через фазовые переменные следующим образом:

(2.9)

Из неравенств (2.9) могут быть найдены полупрямые, являющиеся границами областей с различными типами фазовых траекторий:

(2.10)

Определим первый тип фазовых траектории. Для этого подставим значение z = 5 в уравнение (2.5) и запишем последнее в следующем виде:

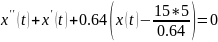(2.11)

Введём новую переменную:

(2.12)

Очевидно, что . Тогда уравнение (2.11) перепишется следующим образом:

(2.13)

Для определения характера фазовых траекторий воспользуемся справочным материалом из методички (рис. 3.1. Виды фазовых траекторий) и представим уравнение (2.13) в виде:

(2.14)

находим, что и . Таким образом, фазовые траектории соответствуют рис. 3.1 (в) методического указания - «Устойчивый фокус»

Рис. 4. Фазовые траектории типа «Устойчивый фокус»

Из (2.12) следует, что , это значит, что фазовый портрет уравнения (2.11) будет отличаться от портрета (2.13) смещением всей картины по оси на величину (+ ).

Второй тип фазовых траекторий отображается по аналогии с первым. Отличие заключается в смещении начала координат фазового портрета по оси на величину (- ).

Качественный фазовый портрет нелинейной системы представлен на (рис. 5), из него следуют, что точки соответствуют устойчивому положению равновесия.

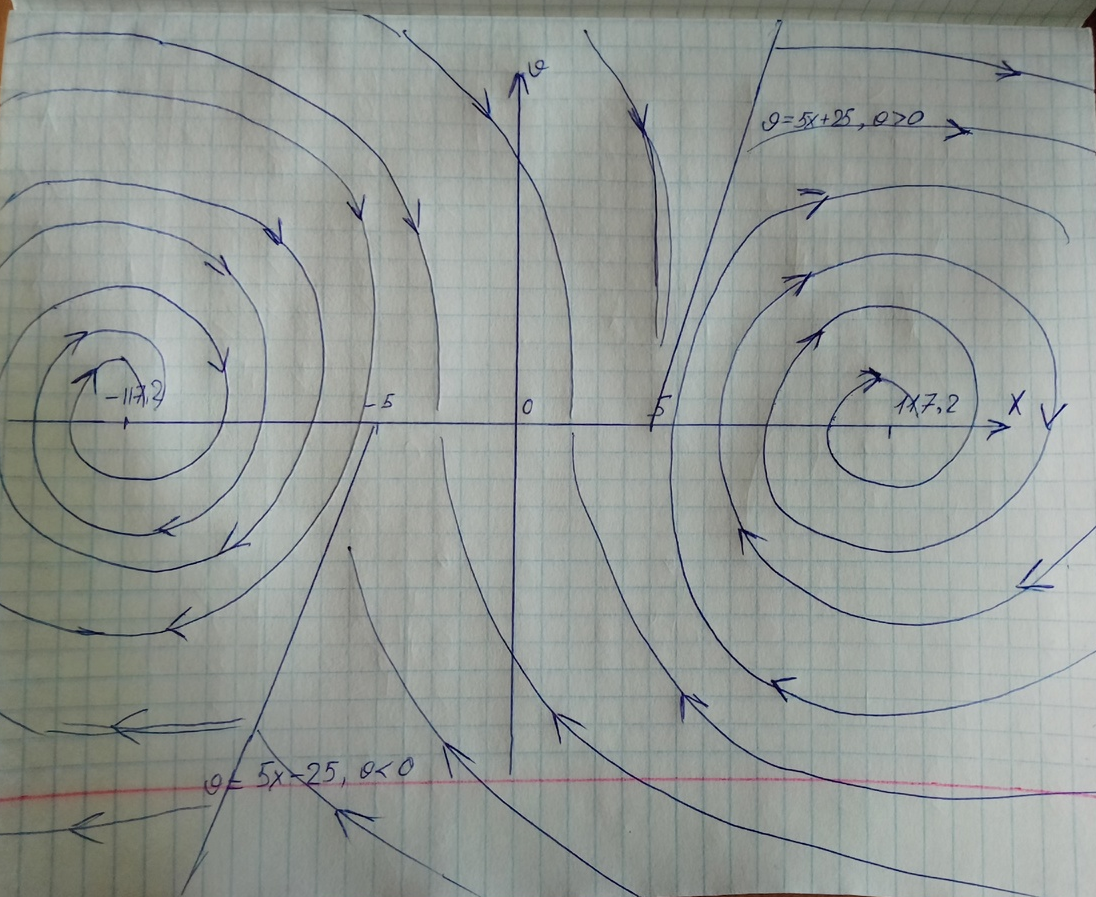
Рис. 5. Фазовый портрет нелинейной системы

2.2. Зададим модель системы (рис. 1.) в ППП MATLAB/Simulink с реализацией моделей звеньев в пространстве состояний.

Преобразуем исходную структурную к виду (рис. 6.), объединив при этом звенья в звено , получим структурную схему вида

Рис. 6. Преобразованная структурная схема исходной системы

В результате можно задать передаточные функции и с помощью модели пространства состояний.

Для

>> g = [0 5];

>> h = [1 1 0.64];

>> [A,B,C,D] = tf2ss(g,h)

A =

-1.0000 -0.6400

1.0000 0

B =

1

0

C =

0 5

D =

0

Для

>> g = [1 0];

>> h = [1 1 0.64];

>> [A,B,C,D] = tf2ss(g,h)

A =

-1.0000 -0.6400

1.0000 0

B =

1

0

C =

1 0

D =

0

Рис. 7. Модель нелинейной системы в MATLAB/Simulink

где, NE3 – блок подсистемы, задающий НЭ3;

W1 – блок усиления, реализующий звено с передаточной функцией ;

W2 – блок, реализующий звено с передаточной функцией в пространстве состояний;

W3v – блок, реализующий звено с передаточной функцией в пространстве состояний;

XX’ Graph – блок для построения фазового портера;

out.v, out.x – блоки, позволяющие передавать и хранить в переменных значения точек v и х для построения фазового портрета;

Scope x(t) – блок для построения графика процесса x(t).

Рис. 8. Модель НЭ 3 с отображением заданных параметров для объекта Relay

Рис. 9. Задание параметров блоков W2, W3v

В новых версиях Simulink после реализации модели системы в workspace возвращается объект выхода, и к переменным x,v мы получаем доступ обращаясь к ним как к свойствам объекта out:

plot(out.x,out.v,'b-');

grid on;

Для построения фазового портера самостоятельно зададим несколько произвольных значений начальных условий и отобразим полученные траектории:

>> x1=out.x;

>> v1=out.v;

>> x2=out.x;

>> v2=out.v;

>> x3=out.x;

>> v3=out.v;

>> x4=out.x;

>> v4=out.v;

>> x5=out.x;

>> v5=out.v;

>> plot(x1,v1,'b-',x2,v2,'r-', x3, v3, "g-", x4, v4, "b-", x5, v5, "r-");

>> grid on

Рис. 10. Фазовые траектории системы

Здесь по оси абсцисс отложена координата х, а по оси ординат – координата 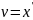. В качестве начальных условий были заданы 5 точек с координатами (x,v): (0,0), (1,-1), (-1,1), (-5,5), (5,-5).

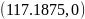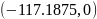В пункте 2.1 исследования точки с координатами и соответствуют устойчивому положению равновесия.

Рис.11. Фазовые траектории для (x,v)=

По графику фазовых траекторий, мы видим, что в системе присутствуют автоколебания.

Зададим самостоятельно ещё три фазовые траектории с начальными условиями согласно пункту 2 задания ( ), ( ) и ( ), и самостоятельно построим для них графики изменения процесса x(t) во времени. На рис. 12 отображены полученные фазовые траектории, а на рис. 13-15 – соответствующие им графики изменения процесса x(t):

Рис.12. Фазовые траектории системы

Рис.13. График процесса x(t) при НУ ( )

Рис.14. График процесса x(t) при НУ ( )

Рис.15. График процесса x(t) при НУ ( )

Как видно из рисунков 13-15, при различных начальных условиях в системе устанавливаются периодические процессы с одинаковыми периодами и амплитудами, то есть данные процессы являются устойчивыми автоколебаниями.