7 сем / Vse_lektsii_TAU

Вводится понятие частных определителей Гурвица:

верхнем углу k строк и k столбцов (главные диагональные миноры).

Выпишем необходимые и достаточные условия устойчивости ИСАУ 1-го и 2-го порядков.

1) Система 1-го порядка ( n 1 ):

ХУ имеет вид: a0e pT a1 0

a0 1 V a1 0

1V

a0 1 V a1 1 V 0

A0V A1 0 (где A0 a0 a1 , A1 a0 a1 )

Условия устойчивости: A0 0 , 1 A1 0

a0 1 2V V 2 a1 1 V 2 a2 1 2V V 2 0

a0 a1 a2 0 , a0 a2 0 , a0 a1 a2 0

Сувеличением порядка ХУ возрастает число неравенств, которые надо проверять вместо критерия Гурвица используют критерии Льенара-Шипара или Рауса.

Предельный коэффициент усиления Kпред – значение коэффициента усиления

разомкнутой системы, при котором замкнутая система находится на границе устойчивости.

3

В расчетном задании оставляем K в Wн (p) → ищем Wз* (p) → по критерию Гурвица смотрим, когда нарушаются неравенства i 0 (обращаются в равенства, если это возможно) → находим Kпред

Найти Kпред для отчета по л.р. № 2.

Пример.

Исследовать на устойчивость линейную ИСАУ с помощью критерия Гурвица, если ее

характеристический полином имеет вид:

A* p e2 pT 3e pT 5.

Решение:

Запишем характеристическое уравнение рассматриваемой ИСАУ:

A* p e2 pT 3e pT 5 0. (*)

Чтобы применить формулировку критерия Гурвица, используемую для непрерывных

всю мнимую ось в бесконечных пределах, поскольку критерий Гурвица предполагает, что корни исследуемого характеристического уравнения лежат на всей комплексной плоскости, а у импульсных систем основные корни характеристического уравнения лежат

а затем применим билинейное преобразование:

z1 V . 1 V

В результате характеристическое уравнение примет вид:

После приведения к общему знаменателю будем иметь:

Для ИСАУ 2-го порядка необходимым и достаточным условием устойчивости по Гурвицу является положительность коэффициентов Ai , i 0, 2 . В рассматриваемом примере

A1 8 0 , а значит, ИСАУ неустойчива.

Ответ: ИСАУ неустойчива.

4

3.2. Частотные критерии устойчивости.

Частотные критерии позволяет судить об устойчивости систем по виду их частотных характеристик. Являются графоаналитическими и имеют простую геометрическую интерпретацию, поэтому широко используются на практике. И на порядок системы не накладываются ограничения, если исследования производятся с помощью программных средств (таких, как MATLAB или mathcad).

В основе частотных критериев устойчивости лежит известный в теории функций комплексного принцип аргумента. Принцип аргумента позволяет выяснить, каким будет

приращение аргумента характеристического вектора A* j исследуемой (замкнутой или

плоскостях P и Z соответственно.

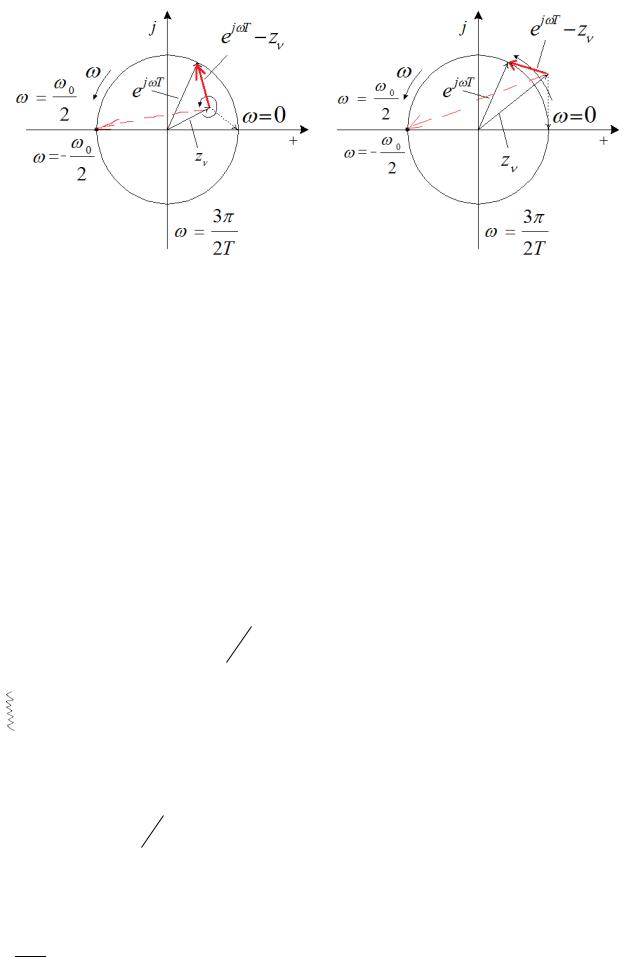
Каждый корень z может быть изображен вектором, проведенным из начала координат к точке z :

характеристического вектора для двух случаев:

1)z лежит внутри окружности единичного радиуса на компл. плоскости Z ;

2)z лежит вне окружности единичного радиуса.

на угол 2 , а во втором – на угол, равный 0 , что следует из нижеприведенного рисунка:

5

Геометрической интерпретацией принципа аргумента является критерий Михайлова А.В.

– позволяет судить об устойчивости системы по виду некоторой кривой, называемой годографом Михайлова (кривой Михайлова).

A* j – характеристический вектор замкнутой или разомкнутой ИСАУ (в зависимости от того, какую ИСАУ проверяем на устойчивость).

Критерий Михайлова А.В.:

Для того чтобы ИСАУ была устойчива, необходимо и достаточно, чтобы при изменении

положительном направлении 2n квадрантов, где n – порядок системы (или иначе – характеристический вектор повернулся на угол n ).

Пример.

а) n 1 A* j a0е j Т a1

6

В отличие от непрерывных систем ИСАУ не только 2-го, но и 1-го порядка могут быть неустойчивы.

б) n 2 A* j a0е2 j Т a1е j Т a2

7

то частное от деления B* (p) на A* (p) будет содержать конечное число членов, а w3 lT –

конечное число ординат, отличных от нуля. Т.е. весовая функция затухнет за конечное число тактов [равное порядку системы n].

Следовательно, условием наличия переходного процесса конечной длительности в замкнутой ИСАУ является:

a0 0 , a1 a2 an 0 (в знаменателе Wз* (p) только одно слагаемое).

Анализ показывает, что такие системы обладают бесконечной степенью устойчивости1 (т.к. в этом случае характеристическое уравнение a0e pnT 0 имеет n корней, равных ).

Глава 4. Синтез линейных ИСАУ.

4.1. Постановка задачи синтеза и способы введения в контур ИСАУ корректирующего звена.

Основными задачами ТАУ являются задачи анализа и синтеза.

Задача анализа сводится к исследованию устойчивости и качества системы.

Задача синтеза заключается в таком выборе структуры и параметров ИСАУ, при котором она устойчива и обладает необходимым качеством (т.е. обеспечиваются требуемые статические и динамические свойства ИСАУ, сформулированные в техническом задании на систему).

Задача синтеза ИСАУ часто сводится к задаче синтеза корректирующего устройства, вводимого в контур системы. Она состоит в определении передаточной функции корректирующего звена ( Wк* (p) ), способа его технической реализации (что это за

устройство), а также места включения в систему, так чтобы обеспечить заданные требования к поведению ИСАУ. (Корректирующее звено позволяет деформировать частотную характеристику разомкнутой ИСАУ и тем самым обеспечить эти требования).

Т.о., постановка задачи синтеза (в узком смысле):

Дано:

1.Матем. модель проектируемой ИСАУ (напр., в виде структурной схемы или W*р (p) ).

2.Требования к поведению ИСАУ, сформулированные в техническом задании на систему (обычно включают в себя устойчивость, конечную длительность переходного процесса (это требование может отсутствовать), заданные значения ошибок в установившемся

режиме ( ст 0ст – для статической системы, кин 0кин – для астатической системы),

времени регулирования ( tрег tрег0 ), перерегулирования ( 0 )).

Исходная ИСАУ не удовлетворяет какому-либо требованию из ТЗ.

1 Степень устойчивости – это расстояние от мнимой оси до ближайшего корня (или пары комплексносопряженных корней) характеристического уравнения устойчивой системы.

2

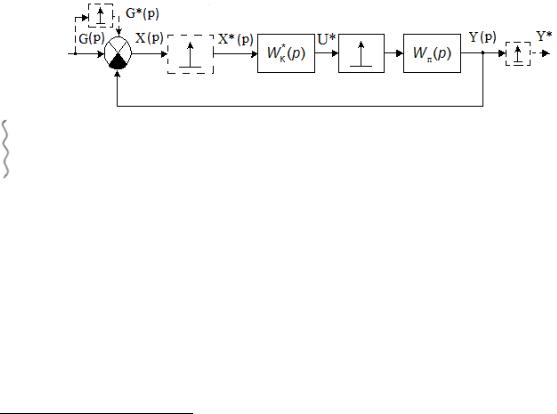
Определить:

передаточную функцию корректирующего звена (КЗ), способ его технической реализации, а также место включения в систему, так чтобы обеспечить заданные требования к поведению ИСАУ.

По месту включения корректирующего звена различают 3 вида коррекции:

последовательная,параллельная

коррекции с помощью обратной связи.

В импульсных системах возможны два варианта реализации КЗ:

1) оно может быть введено в непрерывную часть ИСАУ и реализовано как аналоговое звено. Тогда задача синтеза КЗ решается методами коррекции (синтеза) непрерывных систем.

2) КЗ выполняется как цифровое устройство. В этом случае Wк* (p) определяется методами коррекции (синтеза) импульсных систем.

4.2. Условия осуществимости корректирующего звена и грубости замкнутой ИСАУ.

При решении задачи синтеза ИСАУ необходимо обеспечить условие осуществимости корректирующего звена и условие грубости скорректированной ИСАУ.

Будем решать задачу синтеза для случай, когда КЗ (выполненное как цифровое корректирующее устройство) включается последовательно с приведённой частью:

Wк* (p) – цифровое вычислительное устройство – может стоять до или после ИИЭ, а уравнения относительно выходной величины от этого не изменятся.

U* – управляющее воздействие (сигнал на входе приведенной непрерывной части).

Wп – передаточная функция приведенной непрерывной части = перед. функция неизменяемой части системы.

Для рассматриваемого случая дискретная2 передаточная функция замкнутой ИСАУ относительно Y* (p) имеет вид:

2 слово «дискретная» далее будет опускаться, т.к. это подразумевается

3

Тогда на основании (1) передаточная функция корректирующего звена определяется в форме (подставили в (1) Kз* (p) вместо K* (p) и выразили Wк* (p) ):

Передаточная функцию корректирующего звена Wк* (p) должны быть осуществимой. Это

означает, что реакция КЗ на внешнее воздействие не должна опережать это воздействие (следствие не должно опережать причину).

Передаточная функция корректирующего звена Wк* (p) осуществима, если

mк nк

(степень числителя не превышает степень знаменателя).

Назовём порядком передаточной функции разность степеней знаменателя и числителя

( n m ).

Передаточную функцию Wк* (p) можно реализовать практически (т.е. она осуществима),

если её порядок неотрицателен:

к 0 ,

т.е. степень знаменателя Wк* (p) больше или равна степени числителя.

Когда это будет?

mп nз nп mз

nз mз nп mп

4

з п

–порядок заданной передаточной функции з должен быть не меньше порядка передаточной функции приведенной части п .

–это первое условие осуществимости Wк* (p) .

з

Такое звено коррекции должно обеспечить упреждение на s0 периодов повторения, что физически невозможно. Поэтому второе условие осуществимости Wк* (p) требует, чтобы

при наличии звена запаздывания в приведенной части оно было включено в заданную передаточную функцию синтезируемой системы:

Если даже выполнены условия осуществимости, передаточная функция звена коррекции Wк* (p) (полученная по формуле (2) или (3)) не всегда обеспечивает получение заданной передаточной функции Kз* (p) . Дело в том, что обеспечить практически точное равенство

(2) или (3) невозможно из-за наличия погрешностей, вызванных непостоянством (/вариацией/изменением) параметров приведенной части.

Опр. Если при малых изменениях параметров системы (параметров Wп* (p) и Wк* (p) )

изменения величин, характеризующих состояние системы3, будут также малы, то такую систему называют грубой.

Негрубая система неработоспособна, так как незначительное изменение параметров звеньев ведет к неограниченным изменениям во времени переменных состояния системы.

Для того чтобы замкнутая ИСАУ была грубой, нельзя допускать сокращения правых нулей и полюсов передаточной функции Wп* (p) при помощи передаточной функции

3 выходных переменных или переменных состояния – в зависимости от вида модели

5