1 ВОПРОС. ФУНКЦИЯ. СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ. ГРАФИК ФУНКЦИИ. ОБРАТНАЯ ФУНКЦИЯ. ОСНОВНЫЕ ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ. СЛОЖНАЯ ФУНКЦИЯ. КЛАССИФИКАЦИЯ ФУНКЦИЙ.

Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества. 

Или: Переменная y называется функцией переменной x, если каждое значение x ∈ X, где X – некоторая область изменения переменной х, ставится в соответствие одно определённое значение переменной y ∈ Y, где Y – некоторая область изменения функции у.

Способы задания функции 

1. Аналитический способ: функция задается в виде формулы y=f(x), где переменная – элемент множества значений аргумента, а переменная – соответствующее значение функции.

2. Табличный способ: зависимость задается таблицей значений аргумента и соответствующих им значений функции . Такие функции называют дискретными (заданными в отдельных точках).

3. Графический способ: функция задается с помощью своего графика.

(+Алгоритмический способ: значение функции вычисляется с помощью некоторого алгоритма, на вход которого подается значение аргумента, а на выходе получается значение функции.

+Словесный (описательный) способ: при описательном способе зависимость между и выражается словесным описанием.)

График функции - это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.

Обратная функция: если для функции у=f(x) можно определить функцию x=g(y), ставящую в соответствие каждому значению функции у=f(x) значение её аргумента х, то функция у=g(x) называется обратной функцией к у=f(x) и обозначается y=f^-1(x)

Основные элементарные функции 

1. Постоянная функция: y=c, где с – const

2. Степенная функция: y = x ^α, α ∈ R

3. Показательная функция: y = α ^x, a>0, a ≠ 1;

4. Логарифмическая функция: y = log_ax, a> 0, a ≠ 1;

5. Тригонометрические функции: y = sinx, y = cosx, y = tgx, y = ctgx и обратные им: y = arcsinx, y = arccosx…

Сложная функция - Формально сложная функция определяется как f(g(x)), где f и g - некоторые функции. То есть сначала аргумент x подставляется во внутреннюю функцию g(x), а затем результат подставляется во внешнюю функцию f(). 

2 ВОПРОС. ЛОКАЛЬНО ОГРАНИЧЕННАЯ ФУНКЦИЯ. БЕСКОНЕЧНО МАЛАЯ ФУНКЦИЯ. СВОЙСТВА БЕСКОНЕЧНО МАЛЫХ ФУНКЦИЙ.

Локально ограниченная функция

Функция f(x) называется ограниченной сверху (снизу) на множестве {x}, если найдётся такое вещественное число M (число m), что для всех значений аргумента x из множества {x}справедливо неравенство ( ).

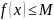Функция называется локально ограниченной в точке , если существует такая окрестность точки , в которой значения функции удовлетворяют неравеству , где и – некоторые числа.

Бесконечно малые функции

Функция 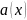называется бесконечно малой в точке x=x₀, если для любой сходящейся к x₀ последовательности {x_n} значений аргумента х отличных от x₀, соответствующая последовательность {a(x_n)} значений функции является бесконечно малой

Свойства бесконечно малых функций

Теорема 1. Сумма и разность бмф есть бмф

Теорема 2. Произведение бмф на бмф есть бмф

Теорема 3. Произведение бмф на функцию, локально ограниченную, есть бмф

3 ВОПРОС. БЕСКОНЕЧНО БОЛЬШИЕ ФУНКЦИИ. ИХ СВЯЗЬ С БЕСКОНЕЧНО МАЛЫМИ.

Бесконечно большие функции

Функция называется бесконечно большой в точке х=х₀ (или при х →х₀), если для любой сходящейся к х₀ последовательности {х_n} значений аргумента х, отличных от х₀, соответствующая последовательность {f(x_n)} значений функции является бесконечно большой

Связь с бесконечно малыми

Если функция f(x) бесконечно большая, то функция 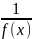является бесконечно малой при х → х₀, и наоборот.

4 ВОПРОС. ПРЕДЕЛ ФУНКЦИИ. ОДНОСТОРОННИЕ ПРЕДЕЛЫ. СВОЙСТВА ПРЕДЕЛА ФУНКЦИИ.

Предел функции

Число А называется пределом функции f(x) в точке х = х₀, если для любой сходящейся к х_о последовательности X₁, X₂, X₃, … Хn… значений аргумента х, отличных от Х₀, соответствующая последовательность f(x1), f(x2), f(x3)..... f(x_n)... значений функции сходится к числу А: lim f(x) = A

Односторонний предел

Предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левым и правым пределами. 

Число A₁ (A₂) называется левосторонним (правосторонним) пределом функции f(x) в точке х = х₀, если для любой сходящейся к х₀ последовательности значений аргумента, элементы x_n которой меньше (больше) х₀, соответствующая последовательность значений функции сходится к А₁ (или А₂). 

 

Свойства пределов функции

1. Предел постоянной величины. Предел постоянной величины равен самой постоянной величине: 

2. Предел суммы. Предел суммы двух функций равен сумме пределов этих функций: 

3. Предел произведения функции на постоянную величину. Постоянный коэффициент можно выносить за знак предела: 

4. Предел произведения. Предел произведения двух функций равен произведению пределов этих функций: 

5. Предел частного. Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю: 

5 ВОПРОС. ТЕОРЕМЫ О ВЫЧИСЛЕНИИ ПРЕДЕЛА ФУНКЦИИ. НЕОПРЕДЕЛЕННОСТИ.

Теорема 1. Предел алгебраической суммы двух, трех и вообще определенного числа функций равен алгебраической сумме пределов этих функций, т.е.

Теорема 2. Предел произведения двух, трех и вообще конечного числа функций равен произведению пределов этих функций:

Следствие 1. Постоянный множитель можно выносить за знак предела

Следствие 2. Предел степени равен степени предела:

Теорема 3. Предел частного двух функций равен частному пределов этих функций, если предел знаменателя отличен от нуля, т.е.

, если  .

Часто при вычислении пределов какой-либо функции, непосредственное применение теорем о пределах не приводит к желаемой цели. Так, например, нельзя применять теорему о пределе дроби, если ее знаменатель стремится к нулю. Поэтому часто прежде, чем применять эти теоремы, необходимо тождественно преобразовать функцию, предел которой мы ищем.

Условные выражения неопределенностей

6 ВОПРОС. ЧИСЛО е. НАТУРАЛЬНЫЕ ЛОГАРИФМЫ.

е = 2,718 281 83 (с точностью до восьмого десятичного знака)

Под числом e понимают предел который невозможно указать точным числом. При этом число e является иррациональным, а значит, оно не может быть корнем какого-нибудь алгебраического уравнения с рациональными коэффициентами.

lnx - натуральный логарифм. Такая запись эквивалентна записи: log_ex = lnx Показательные и логарифмические функции являются обратными, тогда натуральный логарифм, является обратной для функции: y=e^x

7 ВОПРОС. ЗАМЕЧАТЕЛЬНЫЕ ПРЕДЕЛЫ.

1.Первый замечательный предел:

2. Второй замечательный предел:

Вспомогательные пределы:

8 ВОПРОС. СРАВНЕНИЕ БЕСКОНЕЧНО МАЛЫХ. ЭКВИВАЛЕНТНЫЕ БЕСКОНЕЧНО МАЛЫЕ

− если А=0, то α(х) – бмф высшего порядка, по сравнению с β(x)

− если А=∞, то α(х) – бмф более низкого порядка, по сравнению с β(x)

− если А – const, А≠0, то α(х) и β(x) называют бмф одного порядка

− если А=1, то α(х) и β(x) называют эквивалентными α(х) ~ β(x)

9 ВОПРОС. НЕПРЕРЫВНОСТЬ ФУНКЦИИ В ТОЧКЕ. ДВА ОПРЕДЕЛЕНИЯ НЕПРЕРЫВНОСТИ. НЕПРЕРЫВНОСТЬ СУММЫ, ПРОИЗВЕДЕНИЯ, ЧАСТНОГО НЕПРЕРЫВНЫХ ФУНКЦИЙ. НЕПРЕРЫВНОСТЬ СЛОЖНОЙ ФУНКЦИИ. ТИПЫ РАЗРЫВОВ.

Непрерывность функции в точке

Функция f(х) называется непрерывной в точке х₀, если она определена в этой точке и имеет предел, равный значению функции в этой точке:

Два определения непрерывности

По Гейне: Функция f(x) называется непрерывной в точке x₀, если она определена на некоторой окрестности U(x₀) этой точки, и если для любой последовательности {x_n}, сходящейся к x₀: элементы которой принадлежат окрестности U(x₀), последовательность {f(x_n)} сходится к  f(x₀):

По Коши: Функция f(x) называется непрерывной в точке x₀, если она определена на некоторой окрестности U(x₀) этой точки, и если, для любого сколь угодно малого положительного числа ε > 0, существует такое число δ_ε > 0, зависящее от ε, что для всех x, принадлежащих δε - окрестности точки x0: , значения функции принадлежат ε - окрестности точки f(x₀):

Непрерывность суммы, произведения и частного непрерывных функций

Если функции f(x) и g(x) непрерывны в точке х0, то их сумма, произведение и частное (если g(x₀)≠0) являются функциями, непрерывными в точке х₀.

Непрерывность сложной функции

Теорема: Пусть функция t = g(x) непрерывна в точке x₀. И пусть функция f(t) непрерывна в точке t₀ = g(x₀). Тогда сложная функция f(g(x)) непрерывна в точке x₀.

Типы разрывов

Конечная точка x₀ называется точкой разрыва функции f(x), если функция определена на некоторой проколотой окрестности точки x₀, но не является непрерывной в этой точке.

Разрыв 1-го рода: Точка х0 называется точкой разрыва 1-го рода, если в этой точке функция f(x) имеет конечные, но не равные друг другу левый и правый пределы.

Е сли в точке разрыва существуют конечные пределы f(x₀ - 0) и   f(x₀ + 0), то она называется точкой разрыва первого рода, а величина  f(x₀ - 0) -  f(x₀ + 0)  - скачком функции f в точке x₀ (рис 2).

   

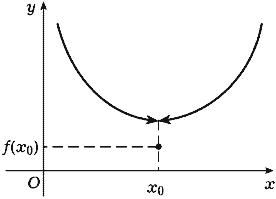
Если скачок функции в точке x₀ равен нулю, то точка x₀ называется точкой устранимого разрыва (рис. 3).

Разрыв 2-го рода:

Е сли один из пределов равен ∞, то это разрыв 2 рода

10 ВОПРОС. НЕПРЕРЫВНОСТЬ ФУНКЦИИ НА ПРОМЕЖУТКЕ. ТЕОРЕМЫ О ФУНКЦИЯХ, НЕПРЕРЫВНЫХ НА ЗАМКНУТОМ ПРОМЕЖУТКЕ

Функция непрерывна на множестве X, если она непрерывна в каждой точке этого множества.

Теоремы:

1. Первая теорема Вейерштрасса. Функция, непрерывная на отрезке, ограничена на этом отрезке, т.е. на отрезке [a, b] выполняется условие – M ≤ f(x)≤ M

2. Вторая теорема Вейерштрасса. Если функция непрерывна на замкнутом промежутке, то она на нем достанет наим. и наиб. значений

3. Первая теорема Больцано - Коши. Если функция f(x)- непрерывная на отрезке [a, b] и имеет на концах отрезка значения противоположных знаков, то существует такая точка внутри этого отрезка, где f(x)=0.

4. Вторая теорема Больцано - Коши. Функция, непрерывная на отрезке [a, b], принимает на этом отрезке все значения между двумя произвольными величинами.

5. Теорема Кантора. Функция, непрерывная на отрезке, равномерно непрерывна на нем. (справедливо только для отрезков, а не для интервалов и полуинтервалов.)

11 ВОПРОС. ЗАДАЧИ, ПРИВОДЯЩИЕ К ПОНЯТИЮ ПРОИЗВОДНОЙ.

Задача об определении скорости точки

Пусть материальная точка движется прямолинейно и неравномерно вдоль

оси Ox по закону x=f(t). Требуется найти ее скорость в момент времени t

Пусть в момент времени t точка находилась в положении M на расстоянии x от начала координат O. За время Δt она, не меняя направления движения, заняла положение M₁ с абсциссой x+Δx. Таким образом, за время Δt путь, пройденный движущейся точкой, изменился на Δx. Очевидно, что , а отношение Δx/Δt определит среднюю скорость точки V_ср за время Δt. Мгновенная скорость точки в момент t равна

Данная формула определяет скорость точки в прямолинейном переменном движении.

1. Задача о касательной

Касательной к плоской кривой K в точке MK называется предельное положение секущей MN при стремлении точки N к точке M вдоль этой кривой.

Пусть кривая K задана уравнением y = f(x). Функция y = f (x) предполагается непрерывной в некоторой окрестности точки x0. Напишем уравнение касательной к кривой K в точке M(x0,f(x0)).

Уравнение прямой, проходящей через точку M(x0,f(x0)), имеет вид: y-f(x0)=k(x-x0), где k = tg,  – угол наклона касательной.

Рассмотрим случай, когда функция y = f (x) строго возрастает в какой-то окрестности точки x0, то есть, если x1<x2, то f(x1)<f(x2). (В случае строгого убывания рассуждения проводятся аналогично)

Угол наклона секущей обозначим через  и вычислим его, воспользовавшись треугольником MNL

Отсюда, так как, следует, что

12 ВОПРОС. ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ ФУНКЦИИ. ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ. УРАВНЕНИЕ КАСАТЕЛЬНОЙ.

_{Определение производной} функции.

Конечный или бесконечный предел отношения приращения функции Δy к вызвавшему его приращению аргумента Δx при условии, что , называется производной функции y=f(x) по переменной x и обозначается

Геометрический смысл производной

Пусть к графику функции y=f(x) в точке с абсциссой x=a можно провести касательную y=kx+b, которая не будет параллельна оси y. Тогда значение производной функции y=f(x) в точке x=a будет выражать угловой коэффициент касательной: k=f’(a)

Так как k=tgα, где α— угол наклона касательной, то верно соответствующее равенство f’(a)= tgα.

Уравнение касательной

y=f(a)+f’(a)(x-a), где

(а; f(a)) – координаты точки касания

13 ВОПРОС. НЕПРЕРЫВНОСТЬ ДИФФЕРЕНЦИРУЕМОЙ ФУНКЦИИ. 

Теорема. Если функция y=f(x) дифференцируема в точке х₀, то она непрерывна в этой точке.

Доказательство.

Однако обратное утверждение смысла не имеет

14 ВОПРОС. ВЫВОД ПРОИЗВОДНЫХ ОСНОВНЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ: СТЕПЕННОЙ, ПОКАЗАТЕЛЬНОЙ, ЛОГАРИФМИЧЕСКОЙ, СИНУСА, КОСИНУСА. 

Степенная функция:

Показательная функция

Логарифмическая функция

Синус

Косинус

15 ВОПРОС. ПРОИЗВОДНАЯ СУММЫ, ПРОИЗВЕДЕНИЯ, ЧАСТНОГО ДВУХ ФУНКЦИЙ. ВЫВОД ПРОИЗВОДНЫХ ТАНГЕНСА И КОТАНГЕНСА.

Простейшие правила дифференцирования

1) (u  v) = u v;

2) (uv) = uv + uv;

3) , если v ≠ 0.

Вывод производной функции y = tg x.

(tg x)' =

Вывод производной функции y = ctg x.

(ctg x)' =

16 ВОПРОС. ТЕОРЕМА О СУЩЕСТВОВАНИИ ОБРАТНОЙ ФУНКЦИИ. ПРОИЗВОДНАЯ ОБРАТНОЙ ФУНКЦИИ. ВЫВОД ПРОИЗВОДНЫХ ОБРАТНЫХ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ

Теорема об обратной функции.

Если функция непрерывна и строго возрастает на отрезке , то на отрезке определена функция , обратная к f, непрерывная и строго возрастающая.

Производная обратной функции

Пусть функция y=f(x) непрерывна и строго монотонна в некоторой окрестности точки x₀, и пусть в этой точке существует производная f′(x₀) ≠ 0. Тогда обратная функция в точке y₀=f(x₀) имеет производную, которая может быть найдена по формуле

Вывод производных обратных тригонометрических функций

Рассмотрим функцию у = arcsinx. Она определена и строго возрастает на интервале [-1,1]. Она служит обратной для функции х=siny, определенной на интервале [-π/2; π/2].

Следовательно,

Аналогично с арккосинусом

Рассмотрим функцию y=arctgx

(f ^-1(x))' = 1/f'(y), где y = f ^-1(x)

(arctg x)' = 1/(tg y)' = 1/(1 + tg² y) = 1/(1 + x²)

Аналогично с арккотангенсом

17 ВОПРОС. ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ

Производная сложной функции равна произведению производной внешней функции, умноженной на производную от внутренней функции.

18 ВОПРОС. ОСНОВНЫЕ ТЕОРЕМЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ (ФЕРМА, РОЛЛЯ, ЛОГРАНЖА И КОШИ) И ИХ ГЕОМЕТРИЧЕСКИЙ СМЫСЛ

Теорема Ферма. Пусть функция y=f(x) определена на отрезке [a, b] а в некоторой внутренней его точке , , достигает наибольшего (или наименьшего) значения. Если в этой точке существует конечная первая производная, то она равна нулю, т.е. .

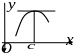
Геометрический смысл теоремы состоит в том, что касательная к графику функции y=f(x) в точке х=с параллельна оси абсцисс.

Теорема Ролля. Если функция y=f(x) непрерывна на отрезке [a, b], дифференцируема в интервале и принимает на его концах равные значения , то внутри интервала существует такая точка , что

Геометрически теорема Ролля означает следующее: если граничные ординаты кривой y=f(x) равны, то на кривой найдется такая точка, в которой касательная параллельна оси абсцисс.

Теорема Коши. Пусть функции и непрерывны на отрезке [a,b] дифференцируемы в интервале и для . Тогда найдется такая точка , в которой справедлива формула

Формула Лагранжа

Является частным случаем формулы Коши

Если функция f непрерывна на отрезке [a; b] и дифференцируема в интервале (a; b), то найдётся такая точка c ∈ (a; b), что

Геометрически это можно переформулировать так: на отрезке [a; b] найдётся точка, в которой касательная параллельна хорде, проходящей через точки графика, соответствующие концам отрезка.

19 ВОПРОС. ДИФФЕРЕНЦИАЛ ФУНКЦИИ. ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ДИФФЕРЕНЦИАЛА. ЕГО СВЯЗЬ С ПРИРАЩЕНИЕМ ФУНКЦИИ. ИНВАРИАНТНОСТЬ ФОРМЫ ДИФФЕРЕНЦИАЛА.

Дифференциалом функции у = f (х) в точке х называется главная часть её приращения, равная произведению производной функции на приращение аргумента, и обозначается dy (или df (x)): dy = f (x)×Dx.

Дифференциал dy называют также дифференциалом первого порядка.

Геометрический смысл дифференциала.

На графике функции у = f (х) возьмем произвольную точку M (x, y) и дадим аргументу x приращение Δx. При этом функция получит приращение Δy (NM₁). Проведем касательную к кривой у = f (х) в точке M и обозначим угол ее наклона к оси OX через α, тогда f‘(х)=tgα. Из треугольника MNP находим PN=MN*tgα=Δx*tgα= f‘(х) Δx, т.е. dy=PN.

Таким образом, дифференциал функции численно равен приращению ординаты касательной, проведенной к графику функции у = f (х) в данной точке, когда аргумент х получает приращение Δx.

Формула дифференциала функции имеет вид dy=f’(x)dx, где dx - дифференциал независимой переменной. Пусть теперь дана сложная функция y=f(g(x)), где u=g(x), y=f(u). Тогда по формуле производной сложной функции находим

, так как g'(x)dx=du.

Итак, dy=f'(u)du, т.е. формула дифференциала имеет один и тот же вид для независимой переменной x и для промежуточного аргумента u, представляющего собой дифференцируемую функцию от x. Это свойство принято называть свойством инвариантности формы дифференциала.

20 ВОПРОС. ПЕРВООБРАЗНАЯ. ТЕОРЕМА О ПЕРВООБРАЗНЫХ.

Функция F(x) называется первообразной для функции f (x) в промежутке, если для всех x справедливо равенство F(x) = f (x).  — такая функция, производная которой равна исходной функции.

Теорема о первообразных. Если функции F(x) и G(x) являются первообразными одной и той же функции f(x) на некотором интервале, то необходимым и достаточным условием этого является то, что G(x) = F(x) + C, где С – любая постоянная. Таким образом, если функция на данном интервале (или отрезке) имеет одну первообразную, то она имеет их бесконечно много, причем все они отличаются друг от друга постоянными слагаемыми.

21 Вопрос

НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ. СВОЙСТВА НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА, СЛЕДУЮЩИЕ ИЗ ОПРЕДЕЛЕНИЯ.

Совокупность всех первообразных функции f(x) на некотором множестве называется ее неопределенным интегралом.

Свойства неопр. интеграла, следующие из определения

1) Дифференциал неопределенного интеграла равен подынтегральному выражению, а производная неопределенного интеграла равна подынтегральной функции

2) Неопределенный интеграл от дифференциала непрерывно дифференцируемой функции равен самой этой функции с точностью до постоянного слагаемого.

Пусть , где φ’(x) непрерывна. φ’(x) является первообразной для φ(x). Поэтому

22 ВОПРОС. ПРОСТЕЙШИЕ СВОЙСТВА НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА.

23 ВОПРОС. ЗАМЕНА ПЕРЕМЕННОЙ В НЕОПРЕДЕЛЁННОМ ИНТЕГРАЛЕ

Пример:

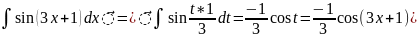
24 ВОПРОС. ИНТЕГРИРОВАНИЕ НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА ПО ЧАСТЯМ

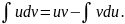
Пример:

25 ВОПРОС. ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ. ЕГО ГЕОМЕТРИЧЕСКИЙ СМЫСЛ.

Криволинейная трапеция – это фигура, ограниченная сверху кривой y=f(x), снизу – отрезком [a;b], слева – прямой х = а, справа – прямой х = b.

Определенный интеграл – площадь криволинейной трапеции

Достаточное условие существование определенного интеграла: если функция y=f(x) непрерывна на [a;b], то она интегрируема на этом отрезке.

Обязательная составляющая криволинейной трапеции – нижнее основание в виде [a;b] и верхняя часть в виде кривой y=f(x).

Геометрический смысл определенного интеграла можно сформулировать следующим образом: определенный интеграл от непрерывной функции равен алгебраической сумме площадей криволинейных трапеций, ограниченных графиком этой функции, осью абсцисс, а также прямыми х = а и х = b. При этом площади криволинейных трапеций, расположенных над осью абсцисс, берутся со знаком (+), а площади трапеций, расположенных под осью абсцисс - со знаком (–).

26 ВОПРОС. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ С ПЕРЕМЕННЫМ ВЕРХНИМ ПРЕДЕЛОМ. ТЕОРЕМА БАРРОУ. ФОРМУЛА НЬЮТОНА-ЛЕЙБИНЦА

Пусть функция f(x) интегрируема на промежутке [a, b]. Возьмем произвольное значение x  [a, b] и рассмотрим определенный интеграл , где переменная интегрирования обозначена через t, чтобы не путать ее с выбранным значением х. Очевидно, что величина указанного интеграла зависит от значения х, т.е. является функцией этого аргумента. Обозначим эту функцию , и назовем ее определенным интегралом с переменным верхним пределом.

Теорема Барроу. Если функция f(x) непрерывна на промежутке , то производная интеграла с переменным верхним пределом равна значению подынтегральной функции, в которой переменная интегрирования заменена значением верхнего предела, т.е.

Основная теорема интегрального исчисления. Если функция f(x) непрерывна на отрезке и - ее любая первообразная на этом отрезке, то имеет место равенство

Эта формула называется формулой Ньютона-Лейбница.

Для краткости записи часто употребляют обозначение (знак двойной подстановки):

. 

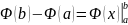27 ВОПРОС. СВОЙСТВА ОПРЕДЕЛЁННЫХ ИНТЕГРАЛОВ, ВЫРАЖЕННЫЕ РАВЕНСТВАМИ.

1.

2.

3.

28 ВОПРОС. СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА, ВЫРАЖЕННЫЕ НЕРАВЕНСТВАМИ. ТЕОРЕМА О СРЕДНЕМ ЗНАЧЕНИИ

1) Если а < b и на промежутке [а, b] функция f(x) интегрируема, причем всюду в [а,b] выполняется неравенство , то имеет место неравенство вида:

2) Если а < b и на промежутке [а, b] функции f(x) и g(х) интегрируемы, причем в [а, b] выполняется неравенство f(x) g(х), то имеем для :

3) Если и на отрезке функция f(x) интегрируема, а т и М – соответственно наибольшее и наименьшее значения функции на отрезке , то имеет место неравенство: