582

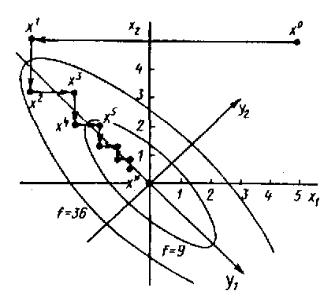
к виду f1(y) = y21+9y22. Очевидно, линии уровня целевой функции – эллипсы y21/9+y22 = c2 (рисунок 6).

Рисунок 6. Графическая иллюстрация метода циклического покоординатного спуска

Результаты расчетов по приведенному выше алгоритму представлены в таблице 12.

Таблица 12

Результаты расчетов по методу циклического покоординатного спуска

71

Из таблицы 12 и рисунка 6 видно, что минимизирующая последовательность {хk} сходится к точке минимума х* = (0,0). Траектория поиска точки минимума в данной задаче имеет ярко выраженный зигзагообразный характер.

Из примера видно, что эффективность решения задачи методом циклического покоординатного спуска можно повысить, если дополнить его алгоритм периодически повторяющимся поиском точки минимума в направлениях pi = xi–xi–1 из точек xi. Так, например, если из точки х4 провести исчерпывающий спуск в направлении p4 = х4– х2 (координаты точек см. в таблице 12), то получим точку (–2,2x10–5; 5,6x10–3), расположенную значительно ближе к точке минимума х*= (0,0), чем точки х5, х6, х7.

Такой подход, состоящий в последовательном нахождении направлений убывания функции и минимизации ее по этим направлениям, лежит в основе ряда алгоритмов. Рассмотрим один из них.

Алгоритм Хука-Дживса

Алгоритм содержит две основные процедуры:

1)исследующий покоординатный поиск в окрестности данной точки, предназначенный для определения направления убывания f (х);

2)перемещение в направлении убывания.

Опишем алгоритм исследующего покоординатного поиска из заданной точки х с приращениями по каждой коорди-

72

5. Положить j = j + 1. Если j n, то перейти к п. 2. В противном случае исследующий поиск окончен – получена точка

удачным. Если при этом норма приращения = ( 1,.., n ) мала, т.е. || || , где – заданная точность, то полагают х*= х. Если заданная точность не достигнута, то полагают = / (постоянная > 1 – коэффициент уменьшения шага) и повторяют исследующий поиск.

Приведем теперь полный алгоритм Хука-Дживса.

1. Выбрать начальную точку х0, вектор приращений= ( 1,.., n), коэффициент уменьшения шага > 1, параметр окончания поиска > 0;

кратить поиск и положить х*= х0. Иначе – положить = / и перейти к п. 1;

Все описанные выше прямые методы безусловной минимизации функции многих переменных содержат детерминированные процедуры поиска точек с меньшим значением функции. Однако разработаны методы минимизации, где в процедуру поиска точек минимума намеренно вводят элементы случайности.

73

4.2 МЕТОДЫ БЕЗУСЛОВНОЙ ОПТИМИЗАЦИИ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

С ИСПОЛЬЗОВАНИЕМ ПРОИЗВОДНЫХ

При использовании прямых методов поиска требуется только вычисление значений функции, но количество этих вычислений может быть очень велико. Методы первого порядка используют информацию о значениях производных функций, то есть дают возможность нахождения стационарных точек, удовлетворяющих необходимому условию первого порядка.

Методы, использующие производные, носят итеративный характер, так как компоненты градиента являются нелинейными функциями.

Пусть функция f(x) дифференцируема в En . В этом разделе рассматриваются итерационные процедуры минимизации вида

где направление убывания рk определяется тем или иным способом с учетом информации о частных производных функции

Так как функция предполагается дифференцируемой, то в качестве критерия останова в случае бесконечной итерационной последовательности {хk}, как правило, выбирается условие ||f '(xk )|| < , хотя могут быть использованы и другие критерии.

Метод градиентного спуска

Положим в (4.3) на каждом шаге рk = –f (xk). Если f (xk) 0, то направление вектора рk является направлением убывания функции f(х), причем в малой окрестности точки xk направление рk обеспечивает наискорейшее убывание этой функции. Поэтому можно найти такое k > 0, что будет обеспечено выполнение условия (4.4).

74

Приведем алгоритм одного из вариантов метода градиентного спуска.

1. Задать параметр точности > 0, начальный шаг > 0, подобрать х En. Вычислить f(х);

2. Найти f '(x) и проверить условие достижения точности ||f'(x)|| < . Если оно выполнено, вычисления завершить, полагая х* = х, f *= f(х). Иначе – перейти к п. 2;

3. Найти y = x– f '(x) и f(у). Если f(у) < f(х), то положить x = у, f(х) = f(у) и перейти к п.1, иначе – перейти к п.3;

4. Положить = /2 и перейти к п. 2.

Замечание. Вблизи стационарной точки функции f(x) величина ||f'(x)|| становится малой. Это может приводить к замедлению сходимости последовательности {хk}. Поэтому иногда в (4.3) полагают pk = – f '(xk)/ ||f '(xk)|| , т.е. вместо f '(xk) используют вектор единичной длины того же направления.

Метод наискорейшего спуска

В этом варианте градиентного метода также полагают pk = –f '(xk) и величина шага k из (4.1) находится в результате решения задачи одномерной минимизации:

Фk( ) min, где Фk( ) = f(xk – f '(хk)), > 0, (4.5)

т.е. на каждой итерации в направлении антиградиента –f '(xk) совершается исчерпывающий спуск.

Опишем алгоритм метода.

1. Задать параметр точности > 0, выбрать х En;

2.Вычислить f'(x) и проверить условие достижения точности: ||f '(x)|| < . Если оно выполнено, то положить х*= х, f*= f(х) и поиск завершить, иначе – перейти к п. 2;

3.Решить задачу одномерной минимизации (4.5) для хk =

х, т.е. найти *. Положить x = x– *f '(x) и перейти к п. 1.

Пример

Рассмотрим функцию f(х) = x21 + 100х22 и используем метод наискорейшего спуска для решения задачи ее минимизации из начальной точки х0 = (1,1).

75

найдем по формуле:

Метод Ньютона

Пусть функция f(x) дважды дифференцируема в En. Тогда для нее можно записать разложение по формуле Тейлора в окрестности точки xk:

f(x) = f(хk) + (f'(хk), x–xk + 21 f (хk)(x–xk), x–xk) + (||x–xk||2). (4.7)

Отсюда видно, что поведение функции f (x) с точностью до величины порядка (||x–xk||2) может быть описано квадратичной функцией:

76

Пусть матрица Гессе f (хk) положительно определена при всех x En и, следовательно, невырождена (detf (хk) > 0). Тогда существует обратная матрица [f (хk)]–1. Отметим, что квадратичная функция (4.7) с положительно определенной матрицей f (хk) сильно выпукла и уравнение (4.8) определяет единственную точку глобального минимума функции Фk(x). Умножим слева обе части равенства (4.8) на матрицу [f (хk)]– 1 и найдем точку минимума xk+1 квадратичной функции (4.7), аппроксимирующей f (x) в окрестности точки x = xk:

xk+1 = xk – [f (хk)]–1 f (хk) , k = 0, 1, … . (4.10)

Итерационный процесс, начатый из произвольной точки x0 En, называется методом Ньютона минимизации функции многих переменных.

Очевидно, для квадратичной функции с положительно определенной матрицей A применение метода Ньютона обеспечивает получение точки глобального минимума ровно за один шаг из любой точки x0 En.

Для выпуклой функции, отличной от квадратичной, применение этого метода обеспечивает, как правило, быструю сходимость. Дело в том, что на каждом шаге итерационного процесса (4.9) используется информация о поведении функции f (x) в окрестности точки xk, содержащаяся не только в значениях первых, но и вторых ее частных производных. Поэтому при прочих равных условиях следует ожидать более быструю сходимость метода Ньютона по сравнению с градиентными методами.

При выборе достаточно хорошего начального приближения x0 En минимизирующая последовательность {xk} для сильно выпуклой дважды дифференцируемой функции f (x) сходится к точке минимума с квадратичной скоростью (xk,x*)cq 2k , q (0,1). Если же точка x0 выбрана недостаточно близкой к точке х*, то последовательность соответствует (4.9).

77

Отметим, что даже сходящаяся последовательность {xk} метода Ньютона не всегда обеспечивает монотонное убывание f(x), т.е. неравенство f(xk+1) < f(xk) для некоторых k = 0,1,.. может нарушаться. Этот недостаток устранен в обобщенном методе Ньютонa:

где величина k> 0 находится на каждом шаге из условия исчерпывающего спуска по направлению рk =–[f (xk)]–1 f (xk).

Недостатком метода Ньютона является необходимость вычисления и обращения матрицы Гессе на каждой итерации.

помощью формулы (4.10) получаем x1= x0– k[f (х0)]–1 f (x0) =(–3/16, –1/8). Так как f '(x1) = (0,0), то задача решена: х*= х1. Целевая функция квадратичная, поэтому решение задачи получено за одну итерацию.

Вопросы и задания для самоконтроля

1.Какова сущность прямых методов минимизации функции нескольких переменных?

2.Дайте характеристику метода минимизации по правильному симплексу.

3.Представьте алгоритм метода минимизации по правильному симплексу.

4.Дайте характеристику метода циклического покоординатного

спуска.

5.Каков алгоритм метода циклического покоординатного спуска?

6.Приведите алгоритм метода Хука-Дживса.

7.Перечислите методы безусловной минимизации функции нескольких переменных с использованием производных.

8.Дайте характеристику метода градиентного спуска.

9.Приведите алгоритм метода градиентного спуска.

10.Дайте характеристику метода наискорейшего спуска.

11.Дайте характеристику метода Ньютона.

78

ВОПРОСЫ ДЛЯ ПОДГОТОВКИ К ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИ

1.Понятия и этапы постановки оптимизационной задачи.

2.Математическая постановка задач оптимизации.

3.Классификация методов оптимизации.

4.Классификация методов математического программирова-

ния.

5.Понятия линейного и целочисленного программирования.

6.Понятия нелинейного, квадратического и дробно-линейного программирования.

7.Понятия дискретного, геометрического и стохастического программирования.

8.Признаки модели линейного программирования.

9.Математическая модель задачи линейного программирова-

ния.

10.Постановка и общий вид задачи оптимального распределения ресурсов при планировании выпуска продукции на предприятии.

11.Постановка и общий вид задачи о смесях (рационе, диете).

12.Алгоритм решения задачи линейного программирования графическим методом.

13.Алгоритм решения задачи линейного программирования симплексным методом.

14.Алгоритм решения задачи линейного программирования методом искусственного базиса (М-методом).

15.Двойственность в линейном программировании.

16.Анализ устойчивости оптимального плана.

17.Постановка транспортной задачи.

18.Методы построения первого опорного плана в транспортной

задаче.

19.Алгоритм решения транспортной задачи.

20.Математическая модель задачи безусловной оптимизации функций одной переменной.

21.Сформулируйте необходимые условия оптимальности в задачах безусловной оптимизации функции одной переменной.

22.Алгоритм классического метода в задачах безусловной оптимизации функции одной переменной.

23.Прямые методы минимизации функций одной переменной.

24.Методы исключения отрезков.

79

25.Особенности метода деления отрезка пополам (дихотомии).

26.Алгоритм метода деления отрезка пополам (дихотомии).

27.Особенности метода золотого сечения.

28.Алгоритм метода золотого сечения.

29.Методы безусловной минимизации функции одной переменной с использованием производных. Особенности метода касательных.

30.Алгоритм метода касательных.

31.Прямые методы безусловной оптимизации функций нескольких переменных. Особенности метода минимизации по правильному симплексу.

32.Алгоритм метода минимизации по правильному симплексу.

33.Алгоритм метода циклического покоординатного спуска.

34.Алгоритм метода Хука-Дживса.

35.Методы безусловной минимизации функции нескольких переменных с использованием производных.

36.Алгоритм метода градиентного спуска.

37.Дайте характеристику метода наискорейшего спуска.

38.Метод Ньютона.

80