
Задача для іспиту, Стешенко
.docxЗадача для іспиту.
Задача. За статистичними даними було проведено дослідження закономірності впливу питомої ваги бобових культур у вартості реалізованої продукції рослинництва (X1 ), середньорічної чисельності працівників (X2 ), площі (X3 ) на урожайність бобових культур (Y). Визначити наявність мультиколінеарності в масиві незалежних змінних X1 , X2 , X3 для рівня значущості α=0,05, n=19 і m=3 за критерієм Пірсона, якщо кореляційна матриця має вигляд :
1 0,8 0,7
r = 0,8 1 0,2
0,7 0,2 1
Розв’язання:
Знаходження кореляційної матриці:
r = X'*X* ,
де X * — матриця нормалізованих пояснювальних змінних;
X'* — матриця, транспонована до матриці X * . Ця матриця симетрична і має розмір 3x3.
Для даної задачі^
1 0,8 0,7
r = 0,8 1 0,2
0,7 0,2 1
Кожний елемент цієї матриці характеризує тісноту зв'язку однієї незалежної змінної з іншою. Оскільки діагональні елементи характеризують тісноту зв'язку кожної незалежної з цією самою змінною, то вони дорівнюють одиниці. Зауважимо, що при знаходженні добутку матриць X'* і X * за рахунок зміщеності коефіцієнтів парної кореляції числові значення діагональних елементів можуть наближатись до одиниці. Якщо це так, то вони заміняються одиницями, а інші значення матриці r збільшуються на величину, що визначається як різниця між одиницею і діагональним елементом.
Інші елементи матриці r дорівнюють:
rx1x2 = 0,8
rx1x3 = 0,7
rx2x3 = 0,2
тобто вони є парними коефіцієнтами кореляції між пояснювальними змінними. Користуючись цими коефіцієнтами, можна зробити висновок, що між змінними x1, x2, x3 існує зв'язок.
Обчислимо детермінант кореляційної матриці r і критерій χ 2 :
r = (-1)¹+¹*1*|1 0,2|+(-1)¹+²*0,8*|0,8 0,2|+(-1)¹+³*0,7*|0,8 1|
|0,2 1| |0,7 1| |0,7 0,2|
= 1,062
x² = -[n-1-1/6(2m+5)]In|r| = -[19-1-1/6(2*3+5)]In1,062= -97/6*In1,062= -0,97
При
ступені свободи
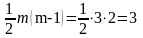 і рівні значущості
і рівні значущості
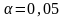 ,
критерій
,
критерій =
1,7.
Оскільки
=
1,7.
Оскільки
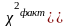 ,
робимо висновок, що в масиві незалежних
змінних мультиколінеарності не існує.
,
робимо висновок, що в масиві незалежних
змінних мультиколінеарності не існує.
Знайдемо матрицю, обернену до матриці r:
С= 17,7 -12,2 -10
-12,2 9,4 6,6
-10 6,6 6,6
Використовуючи діагональні елементи матриці С, обчислимо F-критерії:
F1 = (c11-1)((n-m)/(m-1)) = (17,7 - 1)16/2 = 133,6
F2 = (c22-1)((n-m)/(m-1) = (9,4-1)16/2 = 67,2
F3 = (c33-1)((n-m)/(m-1) = (6,6-1)16/2 = 44,8
Для рівня значущості і (n-m)=15 ступенів вільності і (m-1)=2 критичне (табличне) значення F-критерію F=19,35
Оскільки
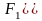 робимо висновок, що
робимо висновок, що
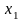 не мультиколінеарна з
не мультиколінеарна з
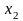 та
та
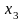 .
.
Оскільки
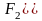 робимо висновок, що
не мультиколінеарна з
та
.
робимо висновок, що
не мультиколінеарна з
та
.
Оскільки
 робимо висновок, що
не мультиколінеарна з
та
.
робимо висновок, що
не мультиколінеарна з
та
.
Обчислимо частинні коефіцієнти кореляції, використавши елементи матриці С:
r12.3 = -C12/√C11*C22 = 12,2/√17,7*9,4= 0,95
r13.2 = -C13/√C11*C33 = 10/√17,7*6,6 = 0,92
r23.1= -C23/√C22*C33 = -6,6/√9,4*6,6 = -0,84, тоді порівняємо
r x1x2 = 0,8<0,95= r12.3 r x1x3 = |0,7|<|0,92| = r13.2 r x2x3 = |0,2|>|-0,84| = r23.1
Частинні коефіцієнти кореляції характеризують тісноту зв’язку між двома змінними за умови, що третя не впливає на цей зв'язок.
Визначимо t-критерій на основі частинних коефіцієнтів кореляції.
t12 = (|r12.3|√n-m)/(√1-r²12.3) = (0,95-√16)/(√1-(0,95)²) = -9,77
t13 = (|r13.2|√n-m)/(√1-r²13.2) = (0,92-√16)/(√1-0,92²) = -7,86
t13 = (|r23.1|√n-m)/(√1-r²23.1) = (-0,84-√16)/(√1-(-0,84)²) = -8,92
Табличне
значення t-критерію
при рівні значущості
і
(n-m)=16
ступенів вільності є t0,05(15)=1,75.
Оскільки
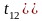 ,
то пара змінних
та
не мультиколінеарна. Оскільки
,
то пара змінних
та
не мультиколінеарна. Оскільки
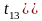 ,
то пара змінних
та
не мультиколінеарна.
,
то пара змінних
та
не мультиколінеарна.
Оскільки
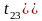 ,
то пара змінних
та
не мультиколінеарна.
,
то пара змінних
та
не мультиколінеарна.
Короткі висновки:
Якщо порушується одна з чотирьох умов, необхідних для застосування 1МНК, а саме коли між пояснювальними змінними існує лінійна залежність, то це явище називається мультиколінеарністю.
Мультиколінеарність негативно впливає на кількісні характеристики економетричної моделі або взагалі робить неможливою її побудову.
Найповніше дослідити мультиколінеарність можна з допомогою алгоритму Фаррара—Глобера.
Цей алгоритм має три види статистичних критеріїв, за якими перевіряється мультиколінеарність усього масиву незалежних змінних (2 – «хі»-квадрат); кожної незалежної змінної з усіма іншими (F-критерій); кожної пари незалежних змінних (t-критерій).
