
КР_1 1 курс 1 семестр [заочка]
.docxКонтрольная работа №1
1.01 Решить систему линейных уравнений методом Гаусса и по формулам Крамера. Сделать проверку.
 .
.
Для решения системы по правилу Крамера найдем следующие определители:

Так как данный определитель не равен нулю, то данная система имеет единственное решение, а значит система совместна.

Тогда решение системы находим по формулам:
x
=
 ; y
=
; y
=

2) Для решения системы методом Гаусса рассмотрим расширенную матрицу системы и приведем ее к треугольному виду:
 = [ умножим первую
строчку на -3, вторую на 5 и сложим их] =
= [ умножим первую
строчку на -3, вторую на 5 и сложим их] =

Т.к. ранг расширенной системы совпадает с рангом системы и равен 2, то система имеет решение.
Тогда получим систему:

Тогда из системы получим решение:

Проверка:

Ответ:
х=
 ,у=
,у=

1.11 Решить систему линейных уравнений тремя методами:
А) по формулам Крамера;
Б) методом Гаусса;
В) с помощью обратной матрицы.

Для решения системы по правилу Крамера найдем следующие определители:

Так как данный определитель не равен нулю, то данная система имеет единственное решение, а значит система совместна.



Тогда решение системы находим по формулам:
х1
=
 =
=
 ;
х2=
;
х2=
 =
=
 ;
х3
=
;
х3
=

2) Для решения системы методом Гаусса рассмотрим расширенную матрицу системы и приведем ее к треугольному виду:
 = [ умножим вторую
строчку на -2 и сложим с первой, умножим
третью строку на -4 и сложим с первой их]
=
= [ умножим вторую
строчку на -2 и сложим с первой, умножим
третью строку на -4 и сложим с первой их]
=
 = [умножим вторую строку на 7, третью на
3 и сложим их ] =
= [умножим вторую строку на 7, третью на
3 и сложим их ] =
 .
.
Т.к. ранг расширенной системы совпадает с рангом системы и равен 3, то система имеет решение.
Тогда получим систему:

3) Для решения
матричным методом нужно рассмотреть
матричное уравнение: AX
= B,
где A
=
 ,
X
=
,
X
=
 ,
B
=
,
B
=
 .
Тогда X
= A-1B.
Найдем матрицу A-1.
.
Тогда X
= A-1B.
Найдем матрицу A-1.
Вычислим
обратную матрицу
 .
.
|
|
|
Тогда
A-1
=

Получим
X
= A-1B
= =
=
 .
.
Ответ: х1 = -4; х2= -3; х3 = 1
1.21 При каких А и В система имеет бесчисленное множество решений? Найдите эти решения.

Определитель матрицы должен быть равен нулю:

Для решения системы методом Гаусса рассмотрим расширенную матрицу системы и приведем ее к треугольному виду:
 = [ умножим первую
строчку на -2 и сложим со второй, умножим
первую строку на -4 и сложим с третьей]
=
= [ умножим первую
строчку на -2 и сложим со второй, умножим
первую строку на -4 и сложим с третьей]
=
 = [умножим вторую строку на -11, третью на
3 и сложим их] =
= [умножим вторую строку на -11, третью на
3 и сложим их] =
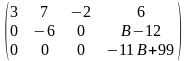 .
.
Тогда
, если
 ,
то система будет
иметь бесконечное множество решений.
,
то система будет
иметь бесконечное множество решений.
 .Значит, при А=-2,
В=9 система имеет бесчисленное множество
решений .
.Значит, при А=-2,
В=9 система имеет бесчисленное множество
решений .

Тогда
получим систему:
 .
Пусть
.
Пусть
 ,
тогда
,
тогда
 ,
,

Ответ: , , ,А=-2, В=9
1.31
Даны вектора
 и
и
 .
Найти
.
Найти
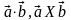 и длину
и длину
 .
.
Векторное
произведение векторов
 , заданных в ортонормированном базисе
, заданных в ортонормированном базисе
 , выражается
формулой:
, выражается
формулой:


Скалярное произведение выражается формулой:


Длина
вектора
 равна
равна


Ответ:
 или
или
 ,
,
 ,
,
1.41 Написать уравнение плоскости, проходящей через точки М(1,2,3), К(-1,3,5), L(0,1,1) в виде Ax+By+Cz+D=0.
 или
или


 – искомое уравнение
.
– искомое уравнение
.
Ответ:
1.51
Даны 4 вектора
 .
Вычислить:
.
Вычислить:
1)координаты
вектора
 в базисе
в базисе
 ;
;
2)
 ;
;
3)
 ;
;
4)
 ;
;
5)
 ;
;
6)
 ;
;
7)
 .
.

Векторы образуют базис в пространстве R3 в том случае, если равенство a + b + c = 0 выполняется лишь тогда, когда = = = 0.
Рассмотрим это условие:
(4;5;2)+ (3;0;1) + (-1;4;2)= (0;0;0) или

Рассмотрим матрицу данной системы и приведем ее к треугольному виду:

 Умножим
первую строчку на -5, вторую на 4 и сложим
их, умножим третью строчку на -2 и сложим
с первой;
Умножим
первую строчку на -5, вторую на 4 и сложим
их, умножим третью строчку на -2 и сложим
с первой;
 умножим третью строку на 15 и сложим
их
умножим третью строку на 15 и сложим
их
 .
.
Так как число ненулевых строк в треугольной матрице равно числу переменных, то система имеет единственное решение, а именно = = . Значит, векторы a, b, c образуют базис. Вектор d в базисе a, b, c имеет вид:
1a + 1b + 1c= d.
В расширенном виде:
Рассмотрим расширенную матрицу системы и приведем ее к треугольному виду (см. предыдущие действия):


 .
.
Получим систему:

Значит,
вектор d
в базисе a,
b,
c
имеет координаты d( ;4;3).
;4;3).
Найдем скалярное произведение :

Найдем скалярное произведение :


Векторное произведение двух векторов а= {ax; ay; az} и b = {bx; by; bz} в декартовой системе координат - это вектор, значение которого можно вычислить, используя следующие формулы:




Ответ:
1) d(
;4;3);
2)14; 3)39; 4)-659;5)
 ;
6)
;
6)
 ;
;
7)115
1.61 Даны вершины треугольника А, В, С. Найти:
1) длину стороны АВ;
2) уравнение стороны АВ;
3) длину медианы АМ;
4) уравнение медианы АМ;
5) уравнение высоты ВН;
6) длину высоты ВН;
7) площадь треугольника;
8) угол ВАС (в градусах);
9) уравнение высоты, параллельной стороне ВС и проходящей через точку А.
В ответах надо приводить уравнения прямых в виде y=kx+b. Все вычисления проводить с двумя знаками после запятой.
А(1,1), В(4,3), С(-4,2)
1) Длина АВ равна

2) Прямая, проходящая через точки А и В:

3)
Найдем середину стороны ВС: Точка M имеет
координаты: ( ;
; )
= (0;5/2). Длина АМ равна
)
= (0;5/2). Длина АМ равна

4) Медиана, проходящая через точки А и М:

5) Найдем уравнение перпендикуляра, опущенного из точки B на прямую AC.
Прямая, проходящая через точки А и C:

Уравнение ВН представляется в виде

Длина перпендикуляра ВН равна

Длина АС равна
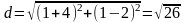
Площадь треугольника будет равна
 ед2
ед2
Для нахождения внутреннего угла необходимо знать уравнения прямых, образующих этот угол.
Прямая,
проходящая через точки А и В:

Прямая,
проходящая через точки А и С:

Тогда, если cos(BAC) равен

Прямая, проходящая через точки С и В:

Тогда
уравнение прямой параллельной стороне
ВС будет выглядеть так:
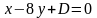 .
Подставим точку А:
.
Подставим точку А:


Ответ:
1)
 ;
2)
;
2)
 ;
3)
;
3)
 ;
4)
;
4)
 ;
5)
;
5)
 ;
6) 2,55; 7)
;
6) 2,55; 7)
 ;
8)
;
8)
 ;
9)
;
9)
 .
.
1.71
Написать уравнение плоскости в виде
Ax+By+Cz+D=0,
проходящей через точку М(1,2,3) параллельно
векторам
 и
и
 .
.
Пусть
необходимо составить уравнение плоскости,
проходящей через заданную точку М0(x0,
y0,
z0) и
параллельную заданным векторам
 и
и  .
Считаем, что такая плоскость построена,
возьмем произвольную точку М(x,y,z) этой
плоскости и составим вектор
.
Считаем, что такая плоскость построена,
возьмем произвольную точку М(x,y,z) этой
плоскости и составим вектор
 .
При любом расположении точки М,
векторы
.
При любом расположении точки М,
векторы  компланарны,
т.е. их смешанное произведение равно 0.
Запишем это условие в векторной форме:
компланарны,
т.е. их смешанное произведение равно 0.
Запишем это условие в векторной форме:  .
Запишем в координатной форме:
.
Запишем в координатной форме:

Для нашего случая получим:


 уравнение
искомой плоскости.
уравнение
искомой плоскости.
Ответ:
1.81 Даны вершины пирамиды SPMN. Найти следующие величины.
1). Длину ребра SN.
2) Уравнение ребра SN.
3) Уравнение грани SPN.
4) Площадь грани SPN.
5) Уравнение высоты, опущенной из вершины S на грань PMN.
6) Длину высоты, опущенной из вершины S на грань PMN.
7) Угол между ребрами SP и SN (в градусах).
8) Угол между ребром SP и гранью PMN (в градусах).
9) Объем пирамиды SPMN.
S (1,0,0), P (0,1,0), M (0,0,2), N (0,4,-1)
1)
Длина ребра SN
равна расстоянию между этими точками,
которое находится по формуле :


2)
Уравнение прямой SN
имеет вид:
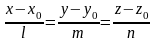 ,
где (x0;y0;z0
) – координаты точки, через которую
проходит прямая, а (l;m;n)
– координаты направляющего вектора.
За координаты (x0;y0;z0
) можно выбрать координаты точки S,
а за направляющий вектор взять вектор
SN
,
где (x0;y0;z0
) – координаты точки, через которую
проходит прямая, а (l;m;n)
– координаты направляющего вектора.
За координаты (x0;y0;z0
) можно выбрать координаты точки S,
а за направляющий вектор взять вектор
SN
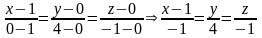 -
уравнение SN.
-
уравнение SN.
3) Уравнение грани SPN получим как уравнение плоскости, проходящей через три точки, а именно
или


 –
Уравнение грани
SPN
–
Уравнение грани
SPN
4) SP =(0-1;1-0;0-0)=(-1;1;0)
SN =(0-1;4 -0;-1-0)=(-1;4;-1)
Площадь грани SPN будет равна
 ед2
ед2
5) Уравнение высоты, опущенной из вершины S на грань PMN
Высота, опущенная из вершины S на грань PMN имеет своим направляющим вектором нормальный вектор плоскости PMN , а значит найдем его.
Уравнение грани PMN получим как уравнение плоскости, проходящей через три точки, а именно
или


 – Уравнение грани
PMN
– Уравнение грани
PMN
Тогда
 -
уравнение высоты, опущенной из вершины
S на грань PMN в симметричном виде.
-
уравнение высоты, опущенной из вершины
S на грань PMN в симметричном виде.
6) Длину высоты, опущенной из вершины S на грань PMN вычислим следующим образом:
 ед
ед
Угол между рёбрами SP и SN равен углу между векторами SP и SN.
SP =(0-1;1-0;0-0)=(-1;1;0)
SN =(0-1;4 -0;-1-0)=(-1;4;-1)
Тогда, если φ угол между векторами SP и SN, то

Тогда

Угол между ребром SP и гранью PMN найдём следующим образом: для начала узнаем уравнение грани PMN , затем выпишем нормальный вектор этой грани, найдём угол между нормалью к грани PMN и вектором SP. Тогда искомый угол между гранью PMN и вектором SP есть разность 900 и полученного последнего угла.
– уравнение грани PMN, SP =(0-1;1-0;0-0)=(-1;1;0)
Значит, нормальный вектор будет иметь координаты N=(-5;0;0). Найдём угол между нормалью к грани PMN и вектором SP.

Тогда

Значит, угол между гранью PMN и вектором SP равен 90-23,070=66,930
Объем пирамиды SPMN.
Объём треугольной пирамиды равен одной шестой объема параллелепипеда, построенного на рёбрах SP , SM, SN.
SP =(0-1;1-0;0-0)=(-1;1;0)
SМ=(0-1;0-0;2-0)=(-1;0;2)
SN =(0-1;4 -0;-1-0)=(-1;4;-1)
Тогда

Ответ:
1) 4.24; 2)
 ;
3)
;
4)
;
3)
;
4)
 ед2;
5)
ед2;
5)
 ;6)1
ед; 7)
;6)1
ед; 7)
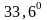 ;
8)
;
8)
 ;
9)
;
9)




