КР_2 1 курс 1 семестр [заочка]

Контрольная работа № 2

2.01 Вычислить комплексное число 𝑧 и найти его модуль

Ответ:

2.11 Решить квадратное уравнение на множестве комплексных чисел

Ответ:

2.21 Дано комплексное число 𝑎. Требуется:

a) записать число 𝑎 в алгебраической, тригонометрической и показательной формах;

б) изобразить 𝑎 на комплексной плоскости;

в) вычислить 𝑎 ¹²;

г) найти все корни уравнения 𝑧 ³ − 𝑎 = 0;

д) вычислить произведение полученных корней;

е) составить квадратное уравнение с действительными коэффициентами, корнем которого, является 𝑎.

А)

Представим число в тригонометрической форме:

В показательной форме:

Б)

В)

Г) Тогда применяя формулу для нахождения корня n-ой степени из числа, получим:

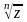= = (cos +isin ); где k = 0, 1, …n-1.

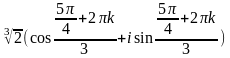= , где k = 0, 1, 2.

Тогда получаем:

W₀ = (cos +isin ),

W₁ = ( cos +isin ),

W₂ = ( cos +isin )

Д)

Е) используем теорему Виетта:

Пусть

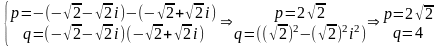
Тогда квадратное уравнение имеет вид :

Ответ: а) , , 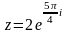; в) ; г) W₀ = (cos +isin ),W₁ = ( cos +isin ),W₂ = ( cos +isin ); д) ; е)

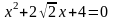
2.31. Для заданной функции найти точки разрыва, если они существуют, и построить график.

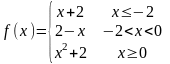
Данная функция определена для всех значений х и на каждом из участков задания (-∞,-2], (-2,0), [0 +∞) является элементарной и, следовательно, непрерывной. Непрерывность функции может нарушиться лишь в точках, где изменяется ее аналитическое значение, то есть в точках х=-2 и х=0. Исследуем эти точки на непрерывность, находя односторонние пределы:

-2

0

При х=1

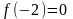
В точке х=-2 f(-2-0) f(-2+0), значит х=-2 точка разрыва. Т.к. правый и левый пределы конечны, то это точка разрыва первого рода.

При х=0

В точке х=0 f(0-0) =f(0+0)= f(0), значит х=0 точка непрерывности.

Построим схематический график.

Ответ: х=-2 точка разрыва первого рода.

2.41 Найти пределы функций

1)

2)

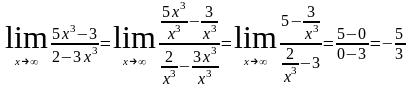
3)

4)

5)

2.51 Найти производные функций.

₁₎

2)

3)

4)

5)

2.61 Найти производные функций.

₁₎

2)

3)

4)

5)

6)

Прологарифмируем обе части уравнения и преобразуем равенство . Пропотенцируем обе части равенства

7)

8)

Дифференцируем обе части равенства, учитывая, что у есть функция от х, получим

2.71 Найти экстремумы и промежутки монотонности функций; построить графики функций

Область определения функции все числа.

Определим критические точки. Для этого найдем производную y'.

. Тогда y' = 0 или =0 имеет решение при х=1/3.

Определим знак первой производной на интервалах.

y'(x)

+ –

1 /3

Значит, на промежутке (-,1/3)– функция возрастает, на промежутке (1/3 ;+ )– функция убывает. Значит, при х=1/3– минимум, у(1/3)=-0,67.

1. Определим точки перегиба. Для этого найдем вторую производную y'' функции:

;

тогда y'' = – не имеет решения. Получим, что перегибов нет. Знак второй производной на области определения всегда отрицательный.

Таким образом, при x  (-; +) график функции выпуклый.

2.81 Исследовать функции методами дифференциального исчисления и построить их графики

1)

1. Найдем область определения D(y). Очевидно D(y) = (–;+).

2. Исследуем функцию на непрерывность.

Значит, y=1 – горизонтальная асимптота.

3. . Функция не является ни четной, ни нечетной.

4. Определим критические точки. Для этого найдем производную y'.

.

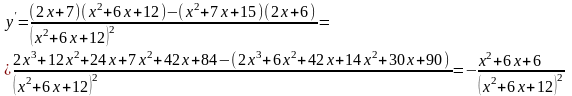Тогда y' = 0 или 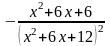=0 имеет решение при х= и х= . Определим знак первой производной на интервалах.

y'(x)

– + –

Значит, на промежутках ( ; ) функция возрастает, на промежутках (-; ), ( ,+ )– функция убывает. Значит, при х= – минимум, у( )=0,71, при х= – максимум, у( )=1,29.

5. Определим точки перегиба. Для этого найдем вторую производную y'' функции:

; тогда y'' = 0 или =0– имеет решение при х=0, х=-6, х=-3. Получим, что это перегибы.

Определим знак второй производной на области определения.

y ''(x)

– + – +

-6 -3 0

Таким образом, при x  (-;-6), (-3;0) график функции выпуклый, при x  (-6;-3), (0;+ ) график функции вогнутый.

6. Выясним, имеет ли функция вертикальные асимптоты y=kx+b.

у=1–горизонтальная асимптота.

7) По результатам исследования строим график функции:

2. 

1. Найдем область определения D(y). Очевидно D(y) = (–;1), (1;+).

2. Исследуем функцию на непрерывность при х=1.

Значит, х=3 – вертикальная асимптота.

3. . Функция не является ни четной, ни нечетной.

4. Определим критические точки. Для этого найдем производную y'.

. Тогда y' = 0 или =0 имеет решение при х=0 и х=2. Определим знак первой производной на интервалах.

y'(x)

+ – – +

0 1 2

Значит, на промежутках (0;1),(1; 2) функция убывает, на промежутках (-;0), (2,+ )– функция возрастает. Значит, при х=2 – минимум, у(2)=-1, при х=0 – максимум, у(0)=-5.

5. Определим точки перегиба. Для этого найдем вторую производную y'' функции:

;

тогда y'' = 0 или =0– не имеет решения. Получим, что перегибов нет.

Определим знак второй производной на области определения.

y ''(x)

+ –

1

Таким образом, при x  (-;1) график функции выпуклый, при x  (1;+ ) график функции вогнутый.

6. Выясним, имеет ли функция вертикальные асимптоты y=kx+b.

у=х-4 -наклонная асимптота.

7) По результатам исследования строим график функции: