
11066
.pdf
100
Окружность вписывалась в квадрат при помощи деления диаметра на семь частей, и приравнивания длины окружности к 22 таким частям. 22/7 = 3.14. Существуют предположения, что восьмерик, традиционный для культовой архитектуры был удобен в разметке: 22:7 = 2,75 и 44:7 = 5,5, еще во времена строительства толосов при переходе от круглой формы к граненой.
Равенство отношений подобных фигур предопределили появление понятия «пропорция», как равенство отношений количественной меры признаков у сравниваемых фигур или элементов одной фигуры. Нахождение крайнего и среднего отношения при делении отрезка, при котором большая его часть является средней пропорциональной между всем отрезком и меньшей частью, определило его по истечению времени как «золотое сечение». Золотое сечение (золотая пропорция,
гармоническое деление) —a и b, b > a, когда справедливо b/a = (a+b)/b. Ф=
b/a = 1.618.
Если длину отрезка принять за единицу, то его части будут выражаться иррациональными числами X = 0,618, а 1 – Х = 0,382. На основе этих чисел может быть получен геометрический ряд:.. - 0,146 – 0,236 – 0,382 – 0,618 – 1 – 1,618 – 2,618 – 4,236 – 6,854 - …, обнаруживаемый при рассмотрении самого широкого круга явлений природы, искусства и архитектуры. Не случайно знаменитый итальянский философ и математик Фра Лука Паччоли называл золотое сечение «божественной пропорцией», а немецкий ученый А. Цейзинг провозгласил золотое сечение универсальной пропорцией, равно характерной для современных творений природы и искусства, есть современные научные данные, что золотая пропорция характерна нее только для роста растений и животных. На наноуровне отношения длины, высоты и диаметра витка ДНК принадлежат тому же ряду отношений. Золотое сечение использовал в своем творчестве И.В. Жолтовский, а Ле Корбюзье положил его в основу своего «Модулора». В современной архитектуре, в массовом строительстве пропорции золотого сечения тяжело применить прежде всего вследствие стандартизации, унификации.
Рис. 85. Геометрическая композиция на основе использования непрерывной пропорции «Золотого» сечения: радиус n-ой окружности равен R=1/Ф^(n-1).

101
Рис. |
86. Измерительная |
шкала |
Рис. |
87. |
Принцип |
построения |
(система |
гармонических |
величин), |
бесконечной |
последовательности |
||
созданная Ле Корбюзье в 1940-х годах, как |
гармоничных интервалов по Ле Корбюзье: |
|||||
инструмент |
пропорционального |
1. Исходный квадрат (abdc) делится на |
||||
построения архитектурных форм. |
|
четыре равные части. |
|
|||
|
|
|
2. В его верхней половине (образующей |
|||
|
|
|
малый "двусмежный квадрат"). |
|
||
Золотое сечение обычно выражают числом 1,618 или обратным ему числом 0,618, для которых ,по предложению Т. Куба и М. Бара приняты символы Ф и 1/Ф. эти числа являются знаменателями возрастающего (Ф) и убывающего (1/Ф) рядов золотого сечения. Интересной особенностью этих чисел является их способность при сложении с единицей (для Ф) и при вычитании из единицы (для 1/Ф) давать квадраты самих себя, т.е. 1+Ф=ФхФ; 1-1/Ф = 1/Фх1/Ф. Ряд чисел золотого сечения – это единственная геометрическая прогрессии, обладающая признаком аддитивного ряда (Ф3= Ф1 + Ф2).
Пропорционирование как метод количественного согласования частей и целого имеет в своей основе геометрическую или числовую закономерность, которая способствует достижению эстетической
102
целостности, гармоничности объемно-пространственной формы за счет объединения ее размеров в какую либо систему.
Особенности пропорциональных систем тесно связаны со способами строительства и измерения, которые применялись архитекторами той или иной эпохи. В древности пропорциональные системы получали с помощью мерного шнура и кольев путем относительно простых геометрических построений на основе треугольника, квадрата, прямоугольника или круга.
В Древнем Египте широко использовалась система пропорционирования на основе «священного египетского треугольника», рассмотренного нами ранее. Система пропорционирования на базе вписанных квадратов давала геометрический ряд с отношением 1:√2, в котором чередовались иррациональные и целые простые числа. Эта система применялась как в Египте, так и в более поздние времена. Например, в средневековье для построения готических башен. Отношения стороны и диагонали квадрата связывают древнерусскую сажень и косую сажень, так называемые «парные меры».
Система вписанных равносторонних треугольников дает ряд на основе двух чередующихся отношений: стороны треугольника к высоте (2/√3) и высоты к половине стороны (1/√3). Пропорционирование на основе равностороннего треугольника особенно широко применялось во времена средневековья, где система триангулирования пронизывала всю структуру готических соборов. Однако отношения, свойственные этой системе, обнаруживаются и в архитектуре других эпох, например, в архитектуре Древней Греции.
«Золотой прямоугольник» может быть построен на базе квадрата при выполнении следующих операций. Из середины основания проводится линия в его правый верхний угол (диагональ двойного квадрата), затем диагональ опускается на линию продолжения стороны основания квадрата, из полученной точки восстанавливаем перпендикуляр до линии продолжения верхней стороны и получаем прямоугольник. Если рассматривать квадрат как часть полученного прямоугольника, то стороны оставшегося прямоугольника будут соотноситься в пропорции золотого сечения. При повторении этой операции несколько раз получаем ряд золотых прямоугольников.
В золотом отношении находятся стороны равнобедренных треугольников с углами 36-, 72- и 72 градусов или 108-, 36- и 36 градусов, поскольку диагонали правильного пятиугольника рассекают его на треугольники именно с такими углами. Ряд золотого сечения может быть получен также на основе пентаграммы – пятиугольной звезды, образованной продлением сторон правильного пятиугольника, также звездчатого десятиугольника. Золотое сечение неоднократно обнаруживалось многочисленными исследователями в памятниках
103
архитектуры Египта, Греции, Рима, Русского и Западноевропейского средневековья, Ренессанса[10].
Числа Фибоначчи (последовательность Фибоначчи) 1, 1, 2, 3, 5, 8,...(a0 = 1, a1 = 1,..., an+2 = an+1 + an) определяются рекуррентными соотношениями его членов, главное свойство заключается в том, что каждый последующий член равняется сумме двух предыдущих. Если же мы попробуем вычислять отношения соседних чисел, то каждый раз будем получать бесконечную дробь, в пределе стремящуюся к золотому числу (чем больше величины, тем ближе к искомому 1,618... или 0,618... в зависимости от того, делим ли мы большее на меньшее или меньшее на большее). Позднее Кеплер и Ньютон доказали, что отношениями численного ряда Фибоначчи определяются радиусы и периоды обращения планет вокруг Солнца, законы небесной и земной механики.
Рекуррентное соотношение, рекуррентный ряд, выражается
формулой, в которой каждый член последовательности алгебраически выражен через предыдущих членов. В том случае, если следующие числа ряда выражены через предыдущих, последовательность называют возвратной. Геометрические и другие виды алгебраических прогрессий – рекуррентные, на основе любого ряда рекуррентных соотношений может быть составлена система пропорциональных членений формы. Возможны ряды на основе геометрическо-арифметической прогрессии, они также являются рекуррентными. Члены арифметической прогрессии образуются путем сложения, геометрической – путем умножения, геометрикоарифметической – комбинированной формулой, в которой присутствуют и множитель, и слагаемое, она может быть представлена в виде многочлена.
Перечисленные системы пропорционирования являются геометрическими, в числовом выражении они менее удобны в использовании, так как включают иррациональные числа. Однако существуют пропорциональные системы, основанные на числовых (арифметических) приемах согласования частей и целого – это так называемые модульные системы, модульные сетки. Простейшим примером модульной системы является масштабная сетка, в которую вписывается как общий абрис, так и детали сооружения, она предполагает наличие модуля – условной единицы измерения. Модульные пропорции широко применялись на протяжении всего развития архитектуры. Наиболее ярким примером модульной системы является построение античных ордеров, в которых в качестве модуля используется либо диаметр, либо радиус колонны. Применяемая в нашей стране модульная система (ЕМС) также использует единый модуль (М=100мм), на основе которого путем его членения или умножения принимают все принятые в строительстве размеры.
Пропорционирование может быть использовано в двух основных направлениях: как метод создания целостной формы и как метод
104
выявления закономерностей построения уже созданных форм. При этом следует понимать, что пропорционирование – достаточно сильное, но далеко не единственное средство гармонизации архитектурной формы и поэтому только одно совершенство пропорций еще не является гарантом получения совершенного архитектурного произведения.
Важна целостность структурно-композиционного каркаса статических и динамических осей формы и согласованность общей структуры и ее производных, составляющих ее элементов. По данным А.В. Шаповала геометрические центры групп симметрии простых правильных тел являются, как правило, центрами их композиционной структуры при визуальном восприятии.
Как правило, такая целостность в крупных масштабах использования не сочетания фигур разного ГВ в линейных либо центрических композициях древности, а в современных достигается при помощи использования сеток, а сетки – производное ряда и пучка линий, предтеча фрактала. В математике сетка опрделяется как частный случай планарного, т.е. не имеющего пересечений, графа.
Для создания эффекта объединения геометрических элементов композиции уровня J при применении к них разных приемов трансформации, рационально объединить их приемами метода синтезации по единой геометрической сетке уровня J+1.
Для акцентирования части (группы геометрических элементов) композиции уровня J, синтезированных на основе монотонной (периодической или регулярной) геометрической сетки, рационально объединить эти геометрические элементы одним приемом трансформации или присвоением качественного иного композиционного простого признака на уровне J-1.
Сетки по соотношениям могут быть: метрические, ритмические, по построению: конечные (как правило, пучковые сетки центрического характера), бесконечные (линейные сквозные).
Центрические, например, тетраксис пифагорейцев, любая мандала и т.д. Могут существовать сетки с периодическим делением, с регулярным делением, делением (членением) на основе ряда, нерегулярным на произвольной основе. Такие сетки расширяются только на основе динамической симметрии.
Линейные сквозные: периодические (метрические - любая такая сетка может быть преобразована во фрактальную), регулярные, квазипериодические, регулярные на основе рядов, прогрессий и т.д., квазирегулярные, нерегулярные сетки. Разновидность фрактальной сетки круговой фрактал — класс геометрических (конструктивных) фракталов, построенных многократным вписыванием в окружность других окружностей меньшего радиуса (итерацией).
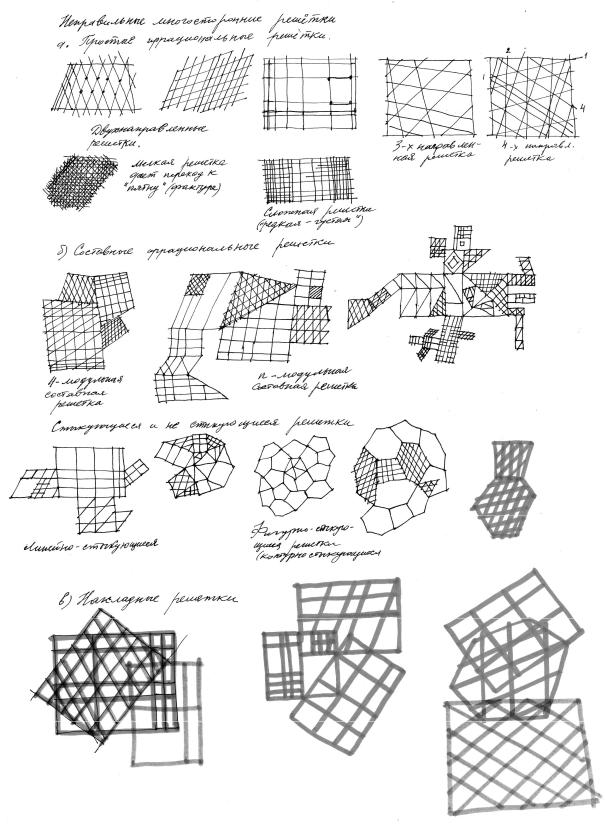
105
Рис. 88. Виды простых иррациональных решеток (сеток) по рукописи Голова Г.М.

106
Рис. 89. А). Заха Хадид Аркитектс, интерьер Башни Восхода Солнца с использованием трехмерной нерегулярной сетки. Б). Декорирование фасада трехмерной квазирегулярной сеткой. В). Жилой дом в Монтенегро, Sanjay Puri Architects, Индия. Объем решен на основе модификации регулярной сетки с равным шагом по вертикали.
Рис.90. а). Конрад Отель в Бейлине, Китай, группа МАD (в перспективе застройки фасады на основе сеток на основе вертикальных и горизонтальных преобладающих членений, комбинированная сетка на основе деформации регулярной структуры). б)
Башня Парка, бюро Farris Architects, ELD partnership, Антверпен, Бельгия.
Могут использоваться сетки с наложением фигур, комбинированные сетки, периодические сетки, трансформированные применением регулярных деформаций (рис.87, таб. 16.).
Сетки – один из инструментов создания оптических иллюзий, связанных с формой. Эффект в 1879 году открыл немецкий физиолог Людимар Герман оптическую иллюзию «мерцающей сетки»: на пересечениях белых линий можно увидеть темные области, хотя в действительности их там нет.

107
Эта иллюзия объясняется латеральным торможением: соседние клетки глаза оказывают друг на друга тормозящее влияние, а мозг, в свою очередь, дополняет изображение собственными образами. Таким образом, глаз не видит полную картину или же видит то, чего на ней на самом деле нет.
Таблица 16.
|
|
|
|
Башня |
10 апартаментов, Париж, |
|
904 Пасифик-стрит / арх. бюро |
регионального |
RMDM Architectes |
|
Loadingdock5 |
дизайна, Майами, |
|
|
|
студия Gang |
|
|
|
Architects |
|
|
|
|
|
|
|
|
|
|
Вариант «сетки Германа»: на |
|
|
|
пересечении линий находятся 12 |
|
|
|
черных точек, однако |
|
|
|
человеческий глаз не может |
Ла Бреа жилой дом эконом класса, арх. Patrick Tighe |
|
||
|
разглядеть их все и сразу. В |
||
+ John V. Mutlow |
|
|
зависимости от |
|
|
|
|
|
|
|
индивидуальных особенностей |
|
|
|
люди видят одновременно лишь |
|
|
|
несколько точек, при этом они |
|
|
|
могут хаотично перемещаются |
|
|
|
по картинке. |
На протяжении истории архитектуры наиболее широкое применение получили центрические комбинированные сетки (центрические, крестовокупольные сооружения) и комбинированные линейные (структуры анфилад, нефов, трансептов и т.п.), на градостроительном уровне – центрические квазирегулярные и комбинированные сетки.

108
В древнем Египте применялись ортогональные градостроительные сетки для плотной упаковки домов в пространстве кварталов простолюдинов.
Рис. 91. Квазифрактальные сетки, вписанные в квадраты с одинаковыми абсолютными метрическими характеристиками, но на основе ячеек разной мерности.
Непериодические паркетные сетки - это и сетки триангуляции, в т.ч.
Делоне (как правило, |
для неплоских поверхностей). Принято считать, что |
метод Т. изобрёл и |
впервые применил В. Снеллиус в 1615—17 при |
прокладке ряда треугольников в Нидерландах для градусных измерений. Работы по применению метода Т. для топографических съёмок в дореволюционной России начались на рубеже 18—19 вв. К началу 20 в. метод получил повсеместное распространение, большое научное и практическое значение. Она служит для: определения фигуры и размеров Земли методом градусных измерений; изучения горизонтальных движений земной коры; обоснования топографических съёмок в различных масштабах и целях; обоснования различных геодезических работ при изыскании, проектировании и строительстве крупных инженерных сооружений, при планировке и строительстве городов и т.д.
При построении Т. исходят из принципа перехода от общего к частному, от крупных треугольников к более мелким.
Триангуляция Делоне — триангуляция для заданного множества точек S на плоскости, при которой для любого треугольника все точки из S за исключением точек, являющихся его вершинами, лежат вне окружности, описанной вокруг треугольника. Обозначается DT(S), описана в 1934 г.советским математиком Борисом Делоне. Из триангуляции Делоне можно перейти в диаграмме Вороного. В 2D для данного множества точек триангуляция Делоне существует (возможно, не одна).
Теорема о триангуляции набора точек. Предположим, что набор точек S
содержит n>3 точек и не все из них коллинеарны. Кроме того, i точек из них являются внутренними (т. е. лежащими внутри выпуклой оболочки CH(S). Тогда при любом способе триангуляции набора S будет получено точно n + i - 2 треугольников. Теорема: Подразбиение Делоне существует, причём для каждого набора точек оно единственно.Триангуляция удобный
ипростой метод описания сложный поверхностей:
∙Эффективная (занимает мало памяти)
∙Универсальная (нет ограничений на дырки или сингулярные ребра)
∙Слишком простая: нет дополнительной информации о границах
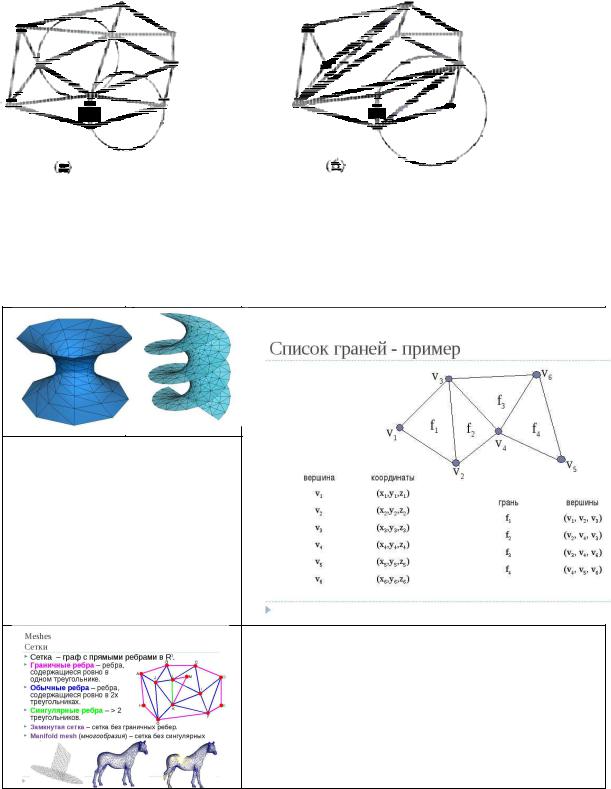
109
Рис. 92. Триангуляция Делоне хорошо сбалансирована: формируемые треугольники стремятся к равноугольности. Так, например, триангуляцию, изображенную на рис. 92а, можно отнести к типу триангуляции Делоне, а на рис. 92б триангуляция содержит несколько сильно вытянутых треугольников и ее нельзя отнести к типу Делоне. На рис. 3 показан пример триангуляции Делоне для набора большого числа точек.
Таблица 17. Применение триангуляции и создаваемые структуры данных:
Поверхность катеноида, смоделированная полигональным методом на основе регулярной сетки триангуляции, поверхность геликоида, полученная на основе той же сетки при помощи топологического преобразования поверхности катеноида.
Структура данных для сетки триангуляции: ∙ Координаты точек ∙ Принадлежность вершин граням
Любые паркеты являются по сути сетками, планарными графами. Для
паркетов из четырехугольников верна теорема: для любого четырехугольника существует паркет, состоящий из четырехугольников,
