10520

120

где - внешнее действующее напряжение.

Функция f ( , ) чаще всего аппроксимируется линейной зависимостью,

иногда – полиномиальной зависимостью [163].

При несомненных достоинствах (простота), данный подход обладает целым рядом недостатков, как и любой подход, не опирающийся на

математические модели процессов и систем.

В работе [69] рассматривается образец материала, выполненный в идее стержня, по которому может распространяться продольная акустическая волна. Считается, что стержень подвергается циклическим испытаниям и в его

материале может накапливаться поврежденность.

Задача является самосогласованной, включающей в себя, кроме

уравнения развития поврежденности (1.2.9.1), которое принимается в виде

где , 1 , 2 - константы, характеризующие поврежденность материала, а так же связь циклических процессов и процессов накопления повреждений,

121

где знак * означает свернутую функцию R(T), являющуюся функцией релаксации:

Уравнение (1.2.9.5) описывает процесс роста поврежденности в зависимости от истории напряжений, и можно утверждать, что постоянная τ >

0 является временем релаксации. Здесь предположено, что история накопления повреждений начинается в момент времени τ = 0, поскольку в начале процесса в материале стержня нет никаких повреждений, (ψ = 0).

В противном случае, если t τ, из уравнения (1.2.9.4), можно получить

зависимость, описывающую процесс роста поврежденности в случае медленного изменения напряжений, в виде:

Используя уравнение (1.2.9.4), перепишем уравнение (1.2.9.3) в виде:

Учитывая классическое уравнение движения:

получаем определяющее уравнение для поврежденной среды в виде:

Описанные с помощью этого уравнения материалы, в которых текущее напряженно-деформированное состояние зависит от истории деформаций,

получили термин «материалы, обладающие памятью».

Модель материала, обладающего памятью, может быть получена путем замены постоянных упругих параметров твердых тел на зависящие от времени операторы. Так, в случае поврежденного материала уменьшается упругий

122

отклик внутренних связей на какое-либо внешнее воздействие,

поврежденность делает материал более деформативным.

Это явление можно учитывать, заменив постоянную величину модуля Юнга математическим оператором [8]:

Здесь Ed – динамический модуль Юнга.

Напротив, в случае медленного нагружения, когда t τ, определяющее уравнение принимает вид:

характеризующий поврежденность материала, изменяющийся в интервале

123

Если ввести в уравнение (1.2.9.14) безразмерные перемещение U u , u0

то это уравнение перепишется в виде:

характеризующая отсутствие повреждений в материале и изменяющаяся в интервале [0;1].

Фундаментальное решение (1.2.9.15) имеет вид уравнения бегущей волны:

где i - мнимая единица, к – волновое число, ω – круговая частота, U 0 -

амплитуда.

Закон дисперсии Φ(к,ω)=0 уравнения (1.2.9.15) определяется из

В случае краевой задачи общее решение уравнения (5.11) имеет следующий вид:

124

В общем случае к и ω являются комплексными величинами. Для анализа дисперсии и затухания волны при рассмотрении краевой задачи, перепишем волновое число к(ω) в виде:

где k=Re(κ) и λ=Im(κ).

Используя эти обозначения, выражение (1.2.9.16) можно переписать

Очевидно, что при положительных значениях λ получаем экспоненциально убывающую волну, распространяющуюся вдоль положительного направления пространственной оси. Другими словами,

спектральные компоненты k(ω)=Re(κ) экспоненциально убывают при X,T→∞

при λ(ω)>0. С другой стороны, если λ(ω)<0, то амплитуды спектральных компонент будут возрастать в геометрической прогрессии. В последнем случае решение линейного уравнения (1.2.9.11) становится неустойчивым при

T>>0.

125

Как обсуждалось выше, в целях изучения распространения волн вдоль оси X, необходимо решить дисперсионное соотношение (1.2.9.13)

относительно волновых чисел κ. Решение находится в следующей форме:

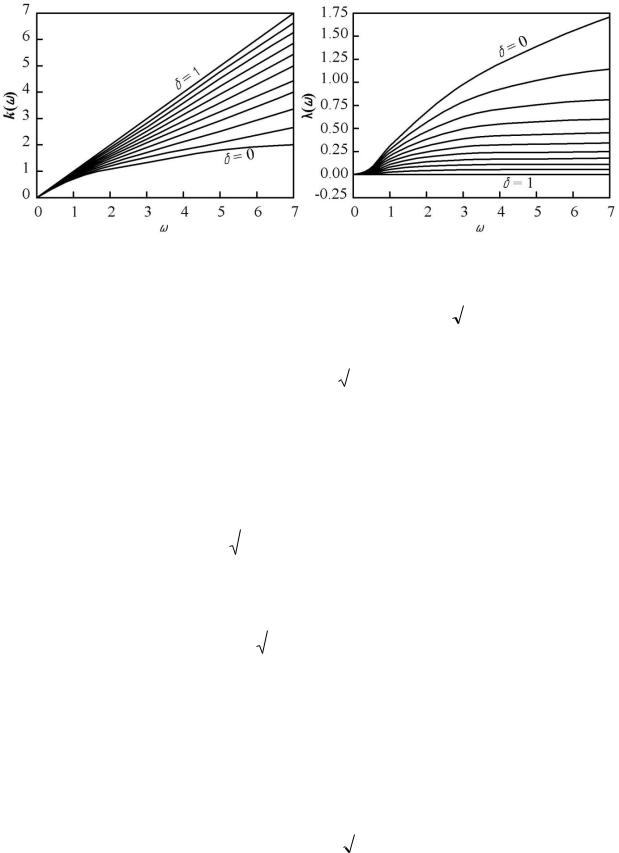
Частотные зависимости k(ω)=Re(κ) и λ(ω)=Im(κ) представлены на рисунке 1.2.9.1 для различных значений параметра δ. Параметр δ принимает значения в интервале δ = [0,1].

Если δ=1, то из (1.2.9.17) и (1.2.9.18) можно найти:

k( ) , ( ) 0. (1.2.9.30)

Это соответствует идеально упругому материалу, в котором отсутствует поврежденность и волна распространяется без затухания.

126

Рисунок 1.2.9.1 - частотные зависимости k(ω)=Re(κ) и λ(ω)=Im(κ) при значениях

параметра δ, лежащих в интервале δ = [0,1]

Для больших частот экспоненциальная постоянная λ зависит только от параметра δ.

Фазовая скорость определяется как vph ( ) k , откуда:

(см.соотношение (1.2.9.30)). Для больших частот фазовая скорость является пределом:

128

Существенное различие между поведением фазовой и групповой скоростей заключается в том, что фазовая скорость является монотонной функцией частоты, а групповая скорость имеет максимум, показанный на рисунке 5.7 пунктирной линией. Сравнение двух скоростей для одного значения δ представлено на рисунке 1.2.9.4. В поврежденном материале групповая скорость больше фазовой скорости при любой частоте. Это означает, что поврежденный материал обладает аномальной дисперсией. Этот факт справедлив и для δ <1, поскольку, как упоминалось выше, если δ=1, то vgr vgr 1, то есть имеет место недисперсионная модель.

Рисунок 1.2.9.4 - графическое cравнение фазовой и групповой скоростей при

фиксированном значении δ

1.2.9.2. Дисперсионный анализ акустической волны, распространяющейся в поврежденном материале

Рассмотрим уравнение (1.2.9.5) со следующими начальными условиями

[63,64]:

где A – амплитуда, γ – пространственный параметр.

Развитие начального (T0=0) возмущения (1.2.9.37), (1.2.9.38),

прослеживается в течении трех последующих моментов времени (рисунок

1.2.9.5).

129

Решение задачи симметрично относительно X=0, потому что начальное значение (1.2.9.37) является четной функцией. Решения, полученные при

δ=0,05, отложены слева от оси симметрии (пунктирная линия), а решения,

полученные при δ = 0,5, отложены справа от нее.

Сравнение приведенных случаев показывает различие в дисперсии

[63,64]. Характер затухания возмущений может изменяться и зависит от величины δ. В случае с малым значением параметра δ (δ = 0,05, что соответствует материалу с критическим уровнем повреждения) затухание происходит гораздо быстрее, чем в случае, когда δ больше (δ = 0,5, что соответствует материалу, исчерпавшему лишь половину своего ресурса). Этот результат согласуется с различиями в дисперсионных участках графиков μ(k).

Начальные участки (при T = T0) в обоих случаях качественно подобны. Это объясняется тем, что в обоих случаях имеет место аномальная дисперсия при больших значениях волнового числа k. Основное различие между представленными случаями возникает при рассмотрении хвостовой части кривых. При малых значениях параметра δ решение ведет себя скорее как решение уравнения диффузии, для больших же значений δ решение ведет себя аналогично решению волнового уравнения. Наличие более громоздкой хвостовой части при малых значениях δ объясняется наложением эффектов нормальной дисперсии, отрицательной групповой скорости и наличием зоны разрыва. При больших значениях параметра δ все эти явления отсутствуют.