10361

A A

и л

ли

Конъюнкцией двух высказываний А и В называется высказывание, обозначаемое A& B (читается: " А и В ''), которое истинно, если истинны оба высказывания A и В, и ложно в остальных случаях (см. таб. 2).

таб. 2

Дизъюнкцией двух высказываний А и В называется высказывание, обозначаемое A B (читается: " А или В ''), которое ложно, когда оба высказывания А и В ложны, и истинно, в остальных случаях (см. таб. 3):

таб. 3

Импликацией двух высказываний А и В называется высказывание, обозначаемое A B (читается: "из A следует В " или "если A , то В ''), которое будет ложным, если А истинно, а В ложно, и истинным в остальных случаях (см. табл. 4):

Большинство теорем в математике может быть представлено в виде импликации A B, где высказывание А является условием теоремы (что дано), а высказывание В является заключением теоремы (оно вытекает из условий, содержащихся в высказывании А). При этом высказывание В называется необходимым условием высказывания А, а высказывание А называется достаточным условием для существования факта, о котором говорится в высказывании В.

Например, утверждение: «Если сумма цифр в десятичной записи целого положительного числа делится на 9, то и само число делится на 9» можно записать в виде импликации A B, где А есть высказывание:

«сумма цифр в десятичной записи целого положительного числа делится на 9», а B есть высказывание: «число делится на 9».

С помощью введенных операций можно строить сложные высказывания в виде формул алгебры высказываний. Рассмотрим, например, формулу:

U: ((A & B) С).

Истинностные значения этой формулы в зависимости от истинностных значений входящих в нее пропозициональных переменных А, В,C приведены в следующей таблице:

Разберем, например, 3-ю строку этой таблицы. Переменные А,В,C принимают соответственно истинностные значения л, и, л. В этом случае

эквивалентными или равносильными, (записывать U V ), если при всех истинностных значениях набора переменных, входящих в эти формулы, эти формулы принимают одинаковые истинностные значения. Например, формулы U: (B & (A A)) и V: В являются эквивалентными, т.е. можно

записать (B & (A A)) B. Действительно. Общий набор переменных этих

формул состоит из двух букв А и В. Приведенная ниже таблица показывает, что при всех истинностных значениях этих переменных формулы U и V принимают одинаковые истинностные значения:

Ниже приведен список основных эквивалентных формул алгебры высказываний, которые принято называть законами

различных свойств элементов или наборов элементов некоторого множества.

Пусть имеется множество M и пусть P есть некоторое свойство, которым могут обладать элементы этого множества. Одноместным предикатом, соответствующим этому свойству, называется функция P(x) ,

определенная на множестве M такая, что

P(a) =1, если a обладает свойством P; P(a) =0, если a не обладает свойством P.

При этом, если для элемента a M имеет место P(a) =1 то говорят, что предикат P(x) истинен на этом элементе, если же P(a) =0, то говорят, что предикат P(x) ложен на этом элементе.

Например, если N есть множество натуральных чисел, а P есть свойство натурального числа быть простым числом, то предикат

P(x) = « x есть простое число»

будет истинным на простых числах и ложным на составных числах. Аналогично, если P есть некоторое свойство, которым могут обладать

наборы (ai1 , ai 2 ,..., ain ) элементов множества M, то n-местным предикатом, соответствующим этому свойству, называется функция P(x1 , x2 ,..., xn ) ,

переменные которой принимают значения на элементах множества M и такая, что

P(ai1 , ai 2 ,..., ain ) 1, если набор (ai1 , ai 2 ,..., ain ) обладает свойством P; P(ai1, ai 2 ,..., ain ) 0, если набор (ai1 , ai 2 ,..., ain ) не обладает свойством P При этом, если P(ai1, ai 2 ,..., ain ) 1 ( P(ai1, ai 2 ,..., ain ) 0), то говорят, что на наборе (ai1 , ai 2 ,..., ain ) предикат P(x1 , x2 ,..., xn ) истинен (ложен).

Пусть, например, R есть множество действительных чисел и пусть на некоторой плоскости введена декартова система координат. Тогда двуместный предикат P(x, y) " x y 1" соответствует свойству точки с

координатами (х,у) лежать на прямой x y 1. На этих точках данный

предикат будет истинным, а на остальных точках плоскости он будет ложным.

Точно так же двуместный предикат O(x, y) " x2 y2 1" истинен на

точках плоскости, которые лежат на окружности радиуса 1 с центром в начале координат.

Предикат P(x1 , x2 ,..., xn ) называется:

1)тождественно истинным на множестве М, если он истинен на любом наборе значений его аргументов;

2)выполнимым на множестве М, если он истинен на некотором наборе значений его аргументов;

3)тождественно ложным на множестве М, если на всех наборах его аргументов он ложный.

Отметим, что свойство предиката быть тождественно истинным, выполнимым или тождественно ложным существенно зависит от множества М.

Так, например, предикат P(x) « x -простое число» является

тождественно истинным на множестве М ={2,5,7,11}, выполнимым на множестве всех целых чисел и тождественно ложным на множестве всех целых четных чисел, больших чем 2.

Пусть P(x1 , x2 ,..., xn ) есть n-местный предикат на множестве М. Тогда с точки зрения алгебры высказываний выражение P(ai1 , ai 2 ,..., ain ) можно

значений переменных (x1 , x2 ,..., xn ) . В связи с этим, к предикатам можно

применять те же операции, что и к высказываниям.

Например, предикат R(x) =« x >1» на множестве натуральных чисел истинен для всех чисел, больших 1. Предикат R(x) "x 1" является отрицанием предиката R(x) и он будет истинен только для x =1.

определены на множестве натуральных чисел. Тогда двуместный предикат

S(x, y) Q(x, y) & R(x, y)

является их конъюнкцией, а двуместный предикат

T (x, y) Q(x, y) R(x, y)

является их дизъюнкцией. Высказывания S(3,5) и T (8,3) будут истинными, а высказывание R(8,3)будет ложным.

Наряду с операциями алгебры высказываний, в логике предикатов существует еще две операции: навешивание квантора существования (обозначается ( ) ) и навешивание квантора общности (обозначается ( )).

Поясним применение и результаты применения этих операций.

Пусть P(x) - одноместный предикат, определенный на множестве М. В

результате навешивания квантора общности по переменной x

получается высказывание

( x)P(x) (читается: для всех x P(x) ),

истинное, когда предикат P(x) истинен на всех элементах множества

М, и ложное в противном случае. Часто в формулах для обозначении квантора общности символ опускается и вместо ( x) пишут просто

(x) .

Врезультате навешивания квантора существования по переменной

xполучается высказывание

( x)P(x) (читается: существует x ,такой что P(x) ),

истинное тогда, когда существует элемент в М, на котором предикат P(x) истинен, и ложное в противном случае). Нетрудно понять, что

для кванторов общности и существования справедливы соотношения

( x)P(x) ( x)P(x) ; ( x)P(x) ( x)P(x)

Рассмотрим несколько примеров. Если на множестве натуральных чисел N рассмотреть два предиката

P(x) = «сумма цифр в десятичной записи числа x делится на 9», Q(x)= «число x делится на 9»,

то в силу известной теоремы высказывания

(x)(P(x) Q(x)) и (x)(Q(x) P(x))

являются истинными.

Если же на множестве натуральных чисел N рассмотреть предикаты P(x) = «десятичная запись целого числа окачивается двумя нулями»,

Q(x)= «число делится на 4»,

то высказывание (x)(P(x) Q(x)) является истинным, а высказывание (x)(Q(x) P(x))является ложным, в силу того, что истинным является высказывание ( x)(Q(x) P(x)) .

Допустим, что P(x, y, z) есть 3-местный предикат на множестве М. Тогда в результате навешивания квантора общности по переменной y

получается двуместный предикат

P1 (x, z) ( y)P(x, y, z) (читается: для всех y P(x, y, z)),

который на паре элементов (ai ,a j ) из множества М будет истинным только в том случае, когда предикат P(x, y, z) истинен на всех наборах вида (ai , y, aj ) , где y любой элемент из множества М.

При навешивании квантора существования по переменной y

получается двуместный предикат

P2 (x, z) ( y)P(x, y, z) (читается: существует y такой что P(x, y, z)),

который на паре элементов (ai ,a j )из множества М будет истинным тогда,

Тогда формула ( x)(P(x) & Q(x, y)) будет соответствовать одноместному

предикату с переменной y, который истинен для всех натуральных чисел, кроме 1 и 2 . А формула

( y)( x)(P(x) & Q( y, x))

фактически соответствует высказыванию, которое утверждает, что для всякого натурального числа найдется простое число, которое его больше. Так как этот факт имеет место, то данное высказывание является истинным.

63.4. Определение математических понятий посредством формул логики предикатов. Как уже говорилось, язык логики предикатов является более выразительным по сравнению с алгеброй высказываний. Многие математические объекты и свойства этих объектов могут быть записаны в виде формул логики предикатов.

Рассмотрим на множестве натуральных чисел предикат:

P(x, y, z) " xy z".

Тогда формула

E(x) ( y)P(x, y, y)

на множестве натуральных чисел будет истинна только, если x 1. Или можно сказать, что эта формула определяет единицу. Если к тому же рассмотреть предикат R(x, y) " x y"то формула

(x)( y)(P(x, y, z) (E(x) & R( y, z) E( y) & R(x, z))

будет истинной только в том случае, когда число z является простым, т.е. эта формула выделяет среди натуральных чисел простые числа.

Ранее, в лекции по теории множеств, нами было введено понятие бинарного отношения В на некотором множестве M. Очевидно, задание бинарного отношения на множестве равносильно заданию некоторого двуместного предиката P на этом множестве. И тогда свойства бинарного отношения могут быть записаны формулами логики предикатов. Вот некоторые из них:

свойство рефлексивности: R = (x)(P(x, x)) ;

свойство симметрии: S = (x)(y)(P(x, y) P( y, x));

свойство транзитивности: T= (x)(y)(z)(P(x, y)&P( y, x) P(x, z)) .

Как указывалось в лекции по теории множеств, бинарное отношение называется отношением эквивалентности, если оно обладает свойствами

рефлексивности, симметрии и транзитивности. А это означает, что соответствующий этому отношению двуместный предикат P обращает в истину конъюнкцию указанных трех формул:

Q R & S &T .

Лекция 64. Элементы теории графов

На языке теории множеств достаточно просто формулировать и анализировать многие задачи, как математического содержания, так и задачи прикладного характера. Точно так же теория графов, с основными понятиями которой нам предстоит познакомиться, дает удобные инструменты для составления математических моделей проблем, возникающих в самых разнообразных сферах исследования: в математике, экономике, биологии, социологии, в сфере коммуникаций и т.д. Причина такой универсальности состоит в том, что математические модели, сформулированные на языке теории графов, отражают самые существенные стороны исследуемых проблем, оставляя в стороне второстепенные детали.

64.1. Определение и основные типы графов. Что же такое граф? Можно сказать, что граф – это есть совокупность точек на плоскости,

некоторые из которых соединены некоторыми линиями, имеющими или не имеющими направления. Точки, о которых идет речь, называются вершинами графа, а соединения между ними можно рассматривать как переходы между вершинами.

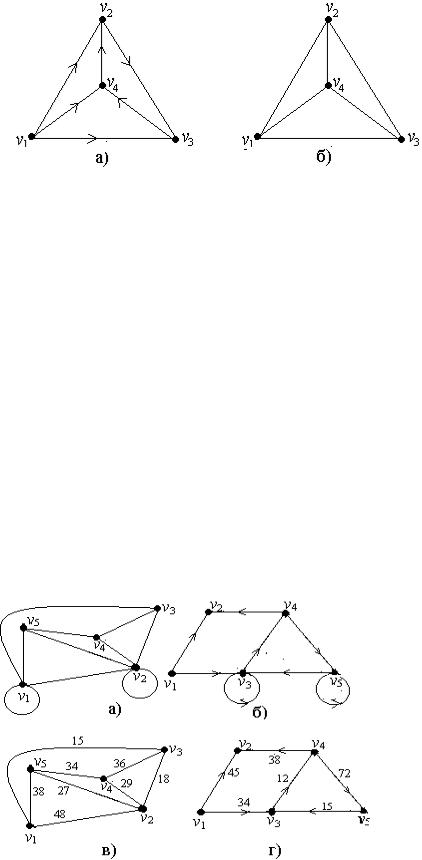
Рис. 64.1

На рис. 64.1 приведены примеры двух основных типов графов. Каждое соединение на рис. 64.1,а снабжено стрелкой, означающей направленность перехода между вершинами. Такого типа соединения называются дугами, а графы такого типа называются ориентированными. На рис. 64.1,б стрелки на соединениях графа отсутствуют. Это означает, что переходы между вершинами возможны в обоих направлениях. Такого типа соединения называются ребрами, а графы с такими соединениями называются

неориентированными.

Графы на рис. 64.2,а и рис. 64.2,б являются графами с петлями, т.к.

взвешенными. Каждое ребро (дуга) в этих графах сопровождается некоторым числом. Эти числа могут означать или пропускную способность ребра (дуги), или расстояния между вершинами, или стоимость перехода между вершинами.

Ориентированные графы служат хорошими моделями при проектировании газотранспортных или электрических сетей или технологий строительства крупных объектов.

Рис. 64.2

В последнем случае вершины графа означают весомые стадии возведения объекта, а дуги означают последовательность выполнения этих стадий. В виде ориентированных или неориентированных графов можно

изображать схемы движения маршрутов городского транспорта, схемы соединений станций метро или пассажирских авиасообщений, блок-схемы алгоритмов, сетки проведения спортивных турниров и т.п. Авторы детективов предваряют содержание произведения построением ориентированного графа, по направлениям дуг которого предполагается развитие задуманного сюжета. В так называемом «графе знакомств» вершинами выступают жители некоторого города (или всего земного шара) и две вершины соединены ребром, в случае, если ассоциированные с ними субъекты знакомы между собой.

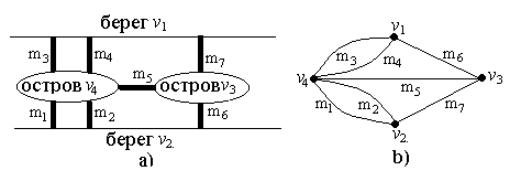
На рис. 64.3,а изображены семь мостов, которые связывали два берега реки и два острова в городе Кенигсберге (современный Калининград). Немецкий философ Иммануил Кант, гуляя по городу, задался вопросом: нельзя ли, начав прогулку с какого-то места, обойти все мосты ровно по одному разу и вернуться в исходное место? Данным вопросом заинтересовался гениальный математик Леонард Эйлер (швейцарец по происхождению, большую часть жизни проработавший в России), и его исследования в поисках ответа оказались отправными в становлении теории графов как самостоятельной математической дисциплины. Приняв берега и острова за вершины, а мосты, их соединяющие, за ребра, Эйлер представил данный городской ландшафт в виде графа, изображенного на рис. 64.3,б. (Обратим внимание на тот факт, что в графе на рис. 64.3,б вершины v4 и v1, а также v4 и v2 соединены не одним, а двумя ребрами. Графы, в которых имеются вершины, соединенные между собой несколькими ребрами, называются мультиграфами.). И теперь вопрос Канта стал звучать так: можно ли из произвольной вершины графа обойти все ребра ровно по одному разу и вернуться в исходную вершину? Ответ, который получил Эйлер, будет сформулирован ниже.

Рис. 64.3

Алгебраически произвольный граф можно представить в виде совокупности G двух множеств V и E (записывается G V , E ), где

V v1 ,v2 ,..., vn есть множество вершин графа, а E есть множество дуг или

множество ребер в зависимости от того ориентированный, граф или

неориентированный. В первом случае каждая дуга из множества E