10289

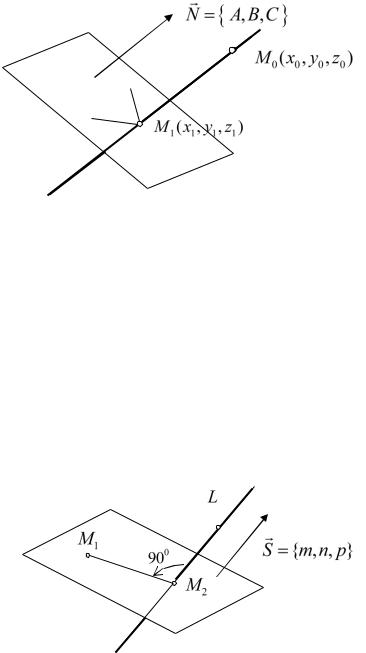
Задача 3.Найти проекцию точки M 0 (x0 , y0 , z0 ) на плоскость

П : Ax By Cz D 0 .

Напомним, что проекцией точки M 0 на плоскость называют основание перпендикуляра M1 , опущенного из этой точки на плоскость (см.

рис.14.3). Очевидно, что эта проекция будет точкой пересечения плоскости П и прямой (14.1), проходящей через точку M 0 перпендикулярно к этой

плоскости.

П

Проекцией точки M1 на прямую L в пространстве служит точка M 2 пересечения прямой L и плоскости, проходящей через данную точку M1 перпендикулярно прямой L (см. рис. 14.4).

Рис.14.4

100

Это подсказывает и путь решения задачи: искомая проекция M 2 находится как точка пересечения плоскости (14.2) и прямой L .

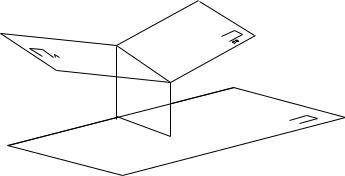
Задача 5.Написать уравнение плоскости, проходящей через заданную точку M 0 (x0 , y0 , z0 ) параллельно двум неколлинеарным векторам

a {a1, a2 , a3} и b {b1,b2 ,b3}.

0

Рис. 14.5

Ясно, что в качестве нормального вектора к требуемой плоскости можно взять векторное произведение данных векторов, т.е.

Тогда уравнение искомой плоскости имеет вид

A(x x0 ) B( y y0 ) C(z z0 ) 0 .

Эту же задачу можно решить и другим способом. Пусть M (x, y, z) – произвольная точка требуемой плоскости. Тогда три вектора M0M , a, b –

Задача 6.Составить уравнение пучка плоскостей, проходящих через данную прямую. Пусть прямая L задана уравнениями

101

A1x B1 y C1z D1 0,A2 x B2 y C2 z D2 0.

Уравнение пучка плоскостей будет иметь вид

в котором – некоторый параметр. Действительно, если точка лежит на данной прямой L , то её координаты обращают в ноль оба уравнения, которыми задана прямая, а, значит, удовлетворяют уравнению (14.3) при любом . Меняя значения , будем получать различные плоскости, проходящие через эту прямую.

Выберем, например, из этого пучка плоскость, перпендикулярную данной плоскости П

Рис. 14.9

Для этого представим уравнение пучка в виде

Из перпендикулярности плоскостей (14.4) и (14.5) следует, что их нормальные векторы взаимно перпендикулярны, т.е.

A1 A2 A3 B1 B2 B3 C1 C2 C3 0 .

Отсюда находим значение , соответствующее искомой плоскости.

Задача 7.Написать уравнение плоскости, проходящей через заданную точку M1 (x1, y1, z1 ) и прямую.

102

Если прямая задана каноническими уравнениями

то задача сводится к предыдущей, если в качестве вектора b взять направляющий вектор прямой, а в качестве другого – вектор a M 0M1 .

Рис. 14.6

Если же прямая задана как пересечение двух плоскостей

A1x B1 y C1z D1 0A2 x B2 y C2 z D2 0 ,

то естественнее воспользоваться уравнением пучка плоскостей «порождённых» этой прямой

A1x B1 y C1z D1 A2 x B2 y C2 z D2 0 .

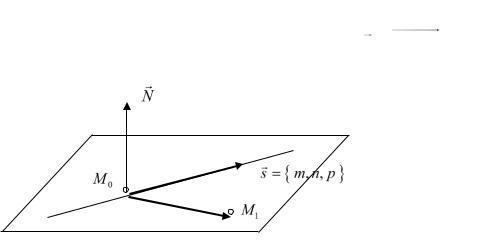
Неизвестное значение определяется из условия прохождения одной из плоскостей этого пучка через данную точку (см. рис. 14.7).

A1x1 B1 y1 C1z1 D1 A2 x1 B2 y1 C2 z1 D2 0.

103

Рис. 14.7

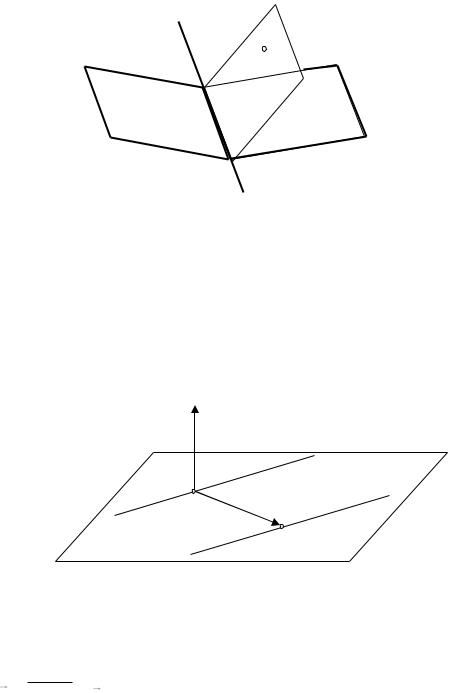
Задача 8.Составить уравнение плоскости, проходящей через две параллельные прямые

= { , , }

0

1

Рис. 14.8

Эта задача также сводится к задаче об уравнении плоскости, проходящей через заданную точку M 0 параллельно двум неколлинеарным

векторам a M0M1 и s m, n, p .

Раздел 4. Математический анализ. Дифференциальное исчисление

Лекция 15. Функция

104

Этот раздел математики изучает функциональные зависимости, которые в окружающем нас мире встречаются на каждом шагу: температура как функция времени, давление как функция высоты и т.д. Так что же такое функция в математическом смысле?

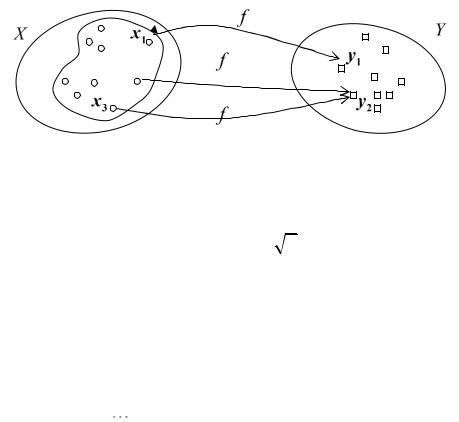
15.1.Функция и способы её задания. Пусть заданы два множества X

иY произвольной природы. Допустим, что каждому элементу x некоторого подмножества D X поставлен в соответствие определенный

элемент y Y . Это соответствие (отображение) называют функцией y от x

называть x аргументом функции, а y – значением функции.

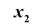
Рис. 15.1

Далее мы будем рассматривать числовые множества X и Y . Примером функции служит зависимость y 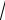x , где X и Y – множества

всех действительных чисел, а область определения и область значения – все неотрицательные числа. В этой функции соответствие f задано операцией

извлечения квадратного корня.

Если функция задана на множестве натуральных чисел, то такая функция называется последовательностью и обозначается символом {an},

который указывает элемент an , соответствующий n . Например, функция факториал an n! 1 2 (n 1) n каждому натуральному числу n

ставит в соответствие число, равное произведению всех натуральных чисел от 1 до n .

Последовательность кроме задания формулой своего общего члена an

может быть задана иначе. Например, указывается несколько её первых членов, а остальные определяются этими заданными членами по тому или иному правилу. Так определяются знаменитые числа Фибоначчи (названные в честь итальянскогоматематикаЛеонардоПизанского (1180–

105

следующий определяется как сумма двух предыдущих, т.е.

an 2 an 1 an .

Функция может быть задана аналитически с помощью одной или нескольких формул, например,

x2 , x 1 y .

2 x, 1 x

Также может быть указан алгоритм, по которому для данного элемента x находится соответствующий ему элемент y (например, E(x) – «целая

часть числа x »: её значения легко находятся E(2) 2, E(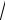2) 1, E( ) 3,

хотя никакой формулой не задаются), или соответствие задано в виде таблицы (например, меню в ресторане), или, наконец, функция может быть задана графически. Под графиком функции в декартовой системе координат понимается множество точек (x, f (x)) .

15.2.Обратная функция.Для данной функции введем понятие

f 1( f (x)) x (см. рис. 15.2)

Рис. 15.2

Интуитивно ясно, что не любые функции имеют обратные, а только те, у которых различным элементам x1 x2 соответствуют различные элементы

f (x1 ) f (x2 ) , т.е. не должно быть ситуации, показанной на рис. 15.1. Если

функция не имеет обратной функции во всей области определения, то она

106

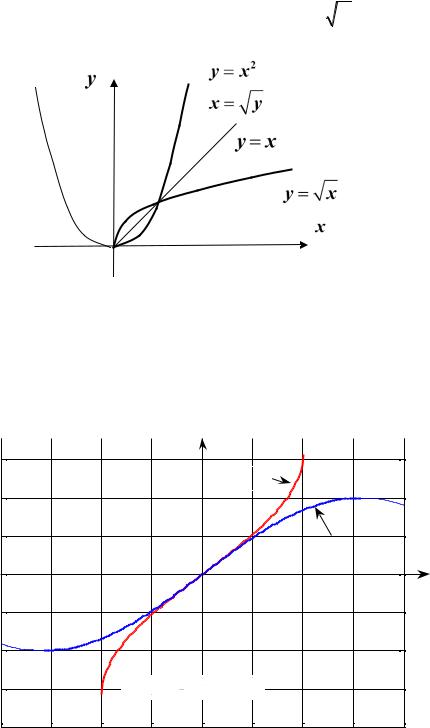
может иметь обратную функцию на некотором подмножестве области

Рис. 15.3

Ясно, что график обратной функции, у которой аргументом является y

, а значением – x , совпадает с графиком данной функции. Однако при построении графика привычно считать аргументом x , а значением – y .

Рис.15.4

В этом случае график обратной функции окажется симметричным графику исходной функции относительно прямой y x . В качестве

примера рассмотрим функцию y sin x , имеющую обратную на интервале

107

/ 2 x / 2 . Обратную к ней называют, как известно, функцию y arcsin x , ее график представлен на рис. 15.4.

15.3. Предел последовательности.Рассмотрим важное понятие предела функции и введем его сначала для функции натурального аргумента, т.е. для последовательности.

Пределом последовательности{ xn } называется конечное число a ,

неравенству (см. рис.15.5 )

a x a

Рис. 15. 5

Тогда понятие предела геометрически означает, что какую бы малую -окрестность точки a мы не взяли, найдется такой номер N , начиная с которого все последующие члены последовательности будут находиться в этой окрестности (см. рис.15.5). Последовательность, имеющая конечный предел, называется сходящейсяили стремящейся к этому пределу, а неимеющая конечного предела – расходящейся.Часто «стремление»

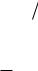
т.е. последовательность модулей отклонения члена последовательности xn

от своего предела a стремится к нулю с увеличением номера n (модуль – лат.modulus –мера).

Примером сходящейся последовательности служит xn 1/ n .

Значит,

lim 1 0 .

n n

Примером расходящейся последовательности служит последовательность xn ( 1)n .

Выше было дано определение предела как некоторого числа, к которомусходится последовательность. Определим так называемые бесконечные пределы. Последовательность называется бесконечно большой, если для любого сколь угодно большого числа M 0 существует такое натуральное число N , что для всех членов последовательности с

символической записи это выглядит так:

lim | xn | ( M 0)( N) ( n N) (| xn | M ) .

n

Среди бесконечно больших последовательностей будем различать последовательности, стремящиеся к бесконечности определённого знака.

Дадим в краткой символической форме определения таких последовательностей:

lim xn ( M 0)( N )( n N ) (xn M ) ,

n

«предел», хотя следует всегда помнить, что символы , не являются

числами, а введены лишь для упрощения записи.

Последовательность, стремящуюся к бесконечности, принято называть бесконечно большой, а последовательность, сходящуюся к нулю,

– бесконечно малой.

Лекция 16.Свойства пределов. Второй замечательный предел

109