Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Нижегородский Государственный Архитектурно-Строительный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

9919

.pdf

Скачиваний:

Добавлен:

25.11.2023

Размер:

3.5 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 189 10 11 12 13 14 15 16 17 18 > Следующая >>>

y sin x

x y 2

y 1 .

y x .

9.118.

9.119.

9.120.

x 0

y 0

x 0

y e

x 1

y 0

9.121.

x 1

9.122.

9.123.

y 1

x 0

В задачах 9.124 - 9.132 вычислить длины дуг кривых:

от точки B 1;1 до точки

A 1;1 .

9.124.

y 2 x

9.125.

y x2 2 между точками пересечения кривой с осью x.

9.126.

y e x между точками с абсциссами x 0

и x 1 .

1 x

9.127.

e e

(цепная линия) между точками с абсциссами

x 1

и x 0 .

x 3t sint

t 2 .

9.128. Циклоиды

y 31 cost

0 t .

9.129. Астроиды x 4cos3t ,

y 4sint

x Rcost tsint

9.130. Эвольвенты окружности

от t1 0

до

y Rsint tcost

9.131. Кардиоиды

31 cos

9.132. Окружности 2 3cosмежду точками, для которых

Глава 10

Дифференциальное исчисление функции нескольких переменных

§1. Область определения функции нескольких переменных

В задачах 10.1 - 10.12 найти и изобразить на координатной плоскости xy области определения функций:

		x 2y						1			1
10.1.	z	x 2y		10.2.		z			.	10.3.	z 2 2	.
10.1.	z		.	10.2.		z	2	2	.	10.3.	z 2 2	.
		x y					x	y			x 4y 4

										2 2
10.4.	z x y 1xy									2 2
10.4.					. 10.5. z 1x 1y.

			z 1			lnxy
10.6.	z lnx y	10.7.
	.				x 2		.

	2	2
	ln1 x y			z y arcsinx 2
10.9.	z	. 10.10.
	y						.

10.12. z lny 4x 8.

lnx y 10.8. z .

y x

10.11. z 1 y2 . sinx

§2. Линии уровня функции нескольких переменных

В	задачах				10.13		- 10.24 написать уравнения линий													уровня функции
z f x;y и построить их:
									z	x				z	y x2						z x y y
									z	x				z	y x2						z x y y
					2																	2
10.13.	z y x .						10.14.			y .			10.15.						. 10.16.
10.13.	z y x .						10.14.			y .			10.15.				2		. 10.16.
																x
	z		y											z x y y
			y					z x y 1												10.20. z x y
			x .					z x y 1
.10.17.			x .		10.18.								. 10.19.				.
.10.21.	z y2 x.						10.22.		z	y		.	10.23.	z		x2		.		10.24. z					2y				.
											3														2y
																	2
										x						y	2									x
										x						y										x
§3. Частные производные функции нескольких переменных
В задачах 10.25 - 10.42									найти частные производные первого порядка:
	z x y												2				3				z	u					v
	z x y												2				3				z
10.25.					.				10.26.				z x 3xy y							10.27.		v					u.
10.25.					.				10.26.								.			10.27.		v					u.
	z			x y									z xtgy 1.								z		2y
10.28.						.			10.29.											10.30.								.
		2			2
		2			2
		x y																					sinx
	z xlny arcsiny													y										y
	z xlny arcsiny												z arctg											y
10.31.								.	10.32.					x.						10.33. z x						.
													81

10.34.	sinx	.				3 2 4
10.34.	z y	.			10.35. z 5x y 1 .
			y
			y			2 2
						2 2
10.37.	z x ln			.	10.38.	z lnx x y.
			x

10.36.z e x .

10.39.u x y z

uxy yz xz

y z

10.40.

10.41.

z .

10.42. u x

u x

В задачах 10.43 - 10.48

найти производные второго порядка

xx ,

yy ,

xy :

3 2 3

10.43. z x xy 5xy.

2 2

10.45. z lnx x y.

10.47. z ylnx .

	1
		2	3
			2
10.44.	z	x y .
	3
		x y
10.46.	z arctg .
		1 xy
10.48.	z arcsinxy
			.

В задачах 10.49 - 10.52 найти смешанные производные указанного порядка от следующих функций:

10.49.	3 z		от z sinx y .	10.50.
10.49.	x y	2	от z sinx y .	10.50.
	x y	2
	2 u
	2 u		2 2 2
10.51.			от u x y z 2xz. 10.52.
10.51.	z y		от u x y z 2xz. 10.52.

	3 z	от	z exy2 .
x 2 y

	3u	от	u exyz.
	x y z

§4. Производные от функций нескольких переменных, заданных неявно

В задачах 10.53 - 10.58			найти производные			dy	от следующих функций:
В задачах 10.53 - 10.58			найти производные			dx	от следующих функций:
						dx
	3 3	4		y x yx
10.53. x y y x a. 10.54. xe ye e 0.
10.55.	x y lny a				3 2
10.55.		.10.56.	cosxy x y 1.
	3 3 3	2	y	x	.
10.57. x y y. 10.58. x				y	.

В задачах 10.59 - 10.66 найти

следующих функций:

2 2 2

x y z

10.59. 2 2 2 1. a b c

2 2 2

10.61. x y z 2xz1.

10.63. e x yz 0.

10.65. sinxyxzyzxyz.

z z

частные производные x , y от

2 2 2

10.60. x 2y 2z 4z0.

3 3

10.62. z 3xyz a.

10.64. e cosxcosy. 10.66. xz lnxyz.

§5. Дифференциал функции нескольких переменных. Применение дифференциала в приближенных вычислениях

10.67. Найти частные дифференциалы первого порядка и полный дифференциал для функций:

	z	x				yx			z x sinxy
	z					yx			z x sinxy
1)		y	;	2)	z e		;	3)	;


2 2						yz
						yz
	5)	yz	;	6)	ux		xyz
4) z lnx y ;	5)	u x	;	6)		x		.
						x

10.68. Для функции		2
		z 3 x y вычислить частный дифференциал d y z
при	x2,y5, y0,01
		.

10.69. Для функции		z lnx y вычислить частный дифференциал	d x z
при	x1,y2, x0,016
		.
10.70. Для функции		z e yx найти значение полного дифференциала	dz при

x1,y1,x0,15,y0,1.

10.71. С помощью дифференциала найти приближенное значение приращения
							M x ;y
функции в точке 0								0		0 :
1)				2		2			M 11;1			x 0,11				y 0,02
		z x 11y 20xy								0 ,	если			,		;
								,		0 ,	если			,		;
				2 2								M 9;3					M9,0;2,96
2) z 2x 3y 5xyпри переходе от точки													0			к точке 1		.
10.72.				С помощью дифференциала найти приближенное значение числового
выражения:
				3,96							3,98

														3)√cos20.05 + 8 0.015;
1) 1,08					;			2) 3,981,03 ;						3)√cos20.05 + 8 0.015;
										2
4)				1,99						2								2
4)		1,04			3,02;			5) 2 22,9492,941,07; 6) 3,02 3,98;
																2
										3						2,03
	3			2		2										2,03
	3			2		2
7)			4,971,061;					8) ln0,111,03;					9)			3		;
															2,031,057
				5,01								1
		arcctg								3	2	5
10)						;		11)		3	2		.
10)						;		11)		2,952,031			.
				4,98						2,952,031

10.73. Высота конуса H = 10 см, радиус основания R = 5 см. Как изменится объём конуса при увеличении высоты на 2 мм и уменьшении радиуса на 2 мм?

10.74. Одна сторона прямоугольника a = 6 дм, другая b = 8 дм. Как изменится диагональ прямоугольника, если a уменьшить на 4 см, а b укоротить на 1 см?

§6. Градиент и производная по направлению функции многих переменных.

10.75. Для функции

z x 2xy3y1найти проекции градиента в точке

1; 2 . Вектор

grad z

построить.

10.76.

Для функции

построить линию уровня и градиент в

z 4 x y

точке

A 1; 2 .

10.77. Для функции

построить линию уровня, градиент функции

x y

в точке

A 1; 2 и найти модуль градиента.

10.78. Для функции

u x y z найти grad u и

gradu

2 2

10.79. Найти производную функции u x y z в точке A 1;1;1 в

направлении l cos45;cos;cos6060.

10.80.

3 2

Найти производную функции zx3xy3xy1в точке

N 3;1 в направлении, идущим от этой точки к точке M 6;5 .

10.81.

Для функции

z f x;y

точке

M x ;y

найти градиент и

0 0

производную по направлению вектора

a :

M 1; 3

a 6;8

1) z 3x 2y,

;

2)	z ln3x 2y					M 1;2
				,		0		,
				y		M 1;1
	z arctg
3)				x ,		0		,
	z	x y				M 1; 2
4)
			2	2 ,		0		,
		x		y
5)				3 3		M	1;3
	z xy x y,					0		,
			2
6)
	z x cosy,					M0 1;		,
7)	z sinx y,							2
						0		,
						M	1;1
8)				2		M	3;4
	z lnx y ,					0		,
	z			x y		M 0;1
9)			2 2		,
						0		,
		x		y 1

a 3; 4 ; a 5;12;

a 1;2 ;

a 2; 1 ; a 5; 12;

a 1; 1 ; a 6; 8 ;

a 1; 1.

10.82. Найти производную по направлению наибыстрейшего роста функции в

точке M x ,y :

0 0 0

	z	1		M 1;1			z ln5x 4y	M 2;1


1)		2	2 ,			2)
1)		2	2 ,	0	;	2)	,	0	;
		x	y
3)	z arctgx y,			0	;	4)		0	;
3)	z arctgx y,			0	;	4)	z x 7y,	0	;
				M 1;1			3	M 1;1
						84

	x	M 1;2			x2 y2		M 2;1
5)	z arcsin	M 1;2		6)	x2 y2	,	M 2;1
5)	,	0	;	6)	z e	,	0 .
	y

10.83. Найти наибольшую крутизну подъёма поверхности:

2 2		6;4;ln100		y	в точке	2;2;4
1) z lnx 4y в точке			; 2) z x			.
10.84. Каково	направление		наибольшего		изменения функции

uxsinz ycoszв начале координат?

10.85. Найти точку, в которой градиент функции z lnx равен

	16		.
i	16	j
i		j
9
				u	1
10.86. Найти производную функции
10.86. Найти производную функции					2 2 2 в направлении её
					x y z
градиента.

§7. Касательная плоскость и нормаль к поверхности

10.87.Составить уравнение касательной плоскости к поверхности, заданной

уравнением Fx,y,z 0(или z f x;y ) в точке M x,y,z :

	2	2		M 1;2;3		2)		2	2	2			M 2;2;3
1)	x y z 80			M 1;2;3			x y z 1						M 2;2;3
1)			,	0	;						,		0	;
3)		2	2	M 1;0;0		4)			2			M 1;y ;3
3)	z lnx y ,			0	;	4)	z 3x y 1,						0 0	;
		4	2					2	2				M 1;2;4
5)	z x 2xyxy M 1;0;2						6)	x y 5 0					M 1;2;4
5)				,	0	;	6)				,		0	;

2 2 2 M 1;2;2

7) xyz4x6y8z10, 0 .

10.88. Cоставить уравнение нормальной прямой к поверхности, заданной

уравнением Fx,y,z 0 (или z f x;y ) в точке M x,y,z :

	2				M 2;1;2					2			2		M 1;1;4
	y z 3 0				M 2;1;2				z 1 x 2y						M 1;1;4
1)	y z 3 0				0	;	2)		z 1 x 2y					,	0	;
1)			,		0	;	2)							,	0	;
	2	2	2						2		2				M 2;1; 1
3)	x 5y z 10M 1; 1;2							4)	z x	y		6			M 2;1; 1
3)				,	0	;		4)						,	0	;
					M 1; 1;1				4				3		M 1;2;9
					M 1; 1;1			z 3x xyy							M 1;2;9
5)				,	0	;	6)	z 3x xyy							0	;
5)				,	0	;	6)							,	0	;
	2 2 2								M 1;2;3
7)	x2y3zyxyz2xz160
7)							,		0 .

§8. Экстремумы функции многих переменных. Наибольшее и наименьшее значения функции в замкнутой области

В задачах 10.89 - 10.102 найти экстремумы функции:

2	2				2	2
		10.90.		7x 12y			.
10.89. z x 4y 8y4.			z e
2	2		2 2
10.91. z x 3y 2x1.		10.92. zx 2y 4y4x2.
2	2					2

10.93. zx xy y2x.		10.94. z yx y x6y.
	2 2			y
		10.96.				2 .

10.95. z 4x y x y.			2
			z e y x
2 2					2 2
10.97. zxyxy96y20. 10.98. z1x y xy6x.
2					3		3
10.99. z99x20y162xy. 10.100.			z x 6xy8y 1.
3	3		3			2 2 2
10.101. z x 3xy y.		10.102. z2x xy 5x y.

В задачах 10.103 – 10.111 найти наибольшее и наименьшее значения функции z f x, y в замкнутой области D :

10.103.

10.104.

10.105.

10.106.

10.107.

10.108.

10.109.

10.110.

10.111.

2 2 z6xy9 9y4x4y,

2 z xyx 2,

2 2 z4xy4x y 8y,

2 2 z2xy y 4x,

2 2 z 3xy5x y,

2 z xy0.5x,

z xy3x y,

z xy3x 2y,

2 z xyx 3x y,

	x 0
			2x .
D :	y

	y 2
		x 0
		y 0 .
D:
		0 x 1

D: .
	0 y 2

	y 0
D:			2 .

		y 4x 4

y x 2

1 x 1

D: .

1 y 1

y 8 D: 2.

y 2x

x 0 D : y 4 .

y x

0 x 4

D: .

0 y 4

0 x 2

D: .

0 y 3

Глава 11

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

§1. Основные понятия и определения

В задачах 11.1 11.11проверить, являются ли решением данных дифференциальных уравнений указанные функции (С – произвольная постоянная).

11.1. y 5x

для

2 y . 11.2.

y x 2 для xy

dx dy 0 .

11.3. y ln cos x для

y tg x .

11.4. y Ce 4 x

для

y 4 y 0 .

11.5. y C x 3 для 3 y x y .11.6.

y x C e x для

y y e x .

11.7. y Ce

для

y 3 y 0 .

11.8. y x

для

y .

11.9. y

С 2

x 2

для x y dx xdy 0 .11.10.

x 2

xy y 2

для

x 2 y y 2x y 0 .11.11. y arctg x y C

для

x y

11.12. Функция

y φ x задана параметрически:

x tet ,

y e t . Докажите,

что эта функция является решением уравнения

1 xy

y 2

0 .

В задачах

11.13 11.18 составить дифференциальные уравнения заданных

семейств кривых( С, С1 , С2 – произвольные постоянные).

11.13. y Cx3 .11.14. x 2 y 2 С 2 .11.15.

x 2 y 2

Cx 0 .

11.16. y sin x C cos x . 11.17.

y C e x C

e x .11.18.

y (C

x)e x .

11.19.Составить дифференциальные уравнение для семейства парабол, с вершиной в начале координат и осью, совпадающей: а) с осью абсцисс, б) с осью ординат.

11.20. Составить дифференциальное уравнение семейства эллипсов, имеющих постоянную большую ось, равную 2a .

11.21. Составить дифференциальное уравнение семейства линий, у которых отрезок касательной между точками касания и осью абсцисс делится пополам в точке пересечения с осью ординат.

В задачах 11.22 11.24 в семействе кривых найти ту, которая удовлетворяет заданным начальным условиям.

11.22. x

С ,

y 0 3 .

11.23. y (C1

C2 x)e

, y 0 1,

y 0 0 .

11.24.

y C1e

C2 e

C3e

, y 0 0

y 0 1

y 0 2 .

В задачах 11.25 11.27 для данного дифференциального уравнения построить поле направлений. Методом изоклин построить приближённо графики интегральных кривых.

11.25. y x 2 .11.26. y x y .11.27. y x 1.

В задачах 11.28 11.32 для данного дифференциального уравнения методом изоклин построить интегральную кривую, проходящую через заданную точку M .

11.28. y y x 2 ,	M 1; 2 .11.29.	y 2 y 2 ,	M 1; 2 .11.30. y xy ,
M 0 ; 1 .11.31.	y x 2 y , M 3; 0 .11.32.		y y x , M 4 ; 2 .

§2. Уравнения с разделяющимися переменными

В задачах 11.33 11.55найти общее решение (общий интеграл) данных дифференциальных уравнений.

11.33. y

.11.34.

.11.35. y

0 .11.36.

0 .

11.37.

y xy 2 0 .

11.38.

.11.39.

xy 2 y 1 .

2x 1

11.40.

x 2 y x 1 0 . 11.41.

xyy 1 x 2 .11.42. y 2 y 1 ctg x .

11.43. 1 y dx 1 x dy 0 .11.44.

y 2 1 dx xydy .11.45.

3 y 2 dx

ydy x2 ydy .

y ln y .

11.46. (

x) y y 0 .11.47.

11.48. y ln y xy 0 .11.49. y 4 e x dy e x dx 0 .11.50. dy y 2 tg xdx 0. 11.51. 6xdx 6 ydy 2x 2 ydy 3xy 2 dx .11.52. y 1 y xy sin x .

		e1 x2		e2x
11.53. 2x 2xy 2	2 x 2 y 0 .11.54.		tg ydx		dy 0 .
				x 1

11.55.y cos x y 1 sin x 0 .

Взадачах 11.56 11.70найти частное решение дифференциального уравнения (задача Коши) удовлетворяющее данным начальным условиям.

		x	2	dy y	2	dx 0 ,				1		1		xdy 1 y			2	dx		0 , y 1	π
11.56.									y				. 11.57.									.
11.56.									y				. 11.57.									.
										2		3									4
11.58. x xy 2 dx x 2 y y dy 0 , y 0 1.11.59. ydx sin 2																				xdy 0 ,
	π					cos	2	xdy cos			2	ydx 0 ,		y 0	π
	π						2				2				π
y		1.11.60.														.11.61.			y	sin xdx dy ,
y		1.11.60.														.11.61.			y	sin xdx dy ,
	2														4
	π					cos x sin ydy cos y sin xdx , y π π .
y		1.11.62.
y		1.11.62.
	2

11.63.1 x2 dy ydx 0 , y 0 e .

11.64.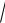1 x 2 dy 1 y 2 dx 0 , y 0 0 .

11.65.	e x dy 2 y dx 0 , y 0 0 .11.66. ln y x dy ydx ,			y 1 1 .
11.67.	e x dy 2x 1 dx 0 , y 0 0 .11.68.	yy	e y 0	, y 1	0 .

		x
11.69.	y xe x y , y 2 2 .11.70. x y 6 1 dx y 2 x 4 1 dy 0 ,				y 0 1.

11.71. Определить и построить кривую, проходящую через точку 2 ; 2 , если

отрезок любой касательной к кривой, заключённый между осями координат, делится точкой касания пополам.

11.72. Определить и построить кривую, проходящую через точку 1; 1 , для

которой отрезок, отсекаемый на оси Ox касательной к кривой в любой её точке, равен квадрату абсциссы точки касания.

11.73. В благоприятных для размножения условиях находится некоторое количество N 0 бактерий. Из эксперимента известно, что скоростьразмножения

бактерий пропорциональна их количеству (коэффициент пропорциональности k>0). Найти зависимость роста числа бактерий N t с течением времени.

11.74. Тело движется со скоростью, пропорциональной пройденному пути. Какой путь пройдёт тело за 5 секунд от начала движения, если известно, что за 1 секунду оно проходит путь 8 метров, а за 3 секунды – 40 метров?

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 189 10 11 12 13 14 15 16 17 18 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
25.11.20233.5 Mб09914.pdf
#
25.11.20233.5 Mб09915.pdf
#
25.11.20233.5 Mб19916.pdf
#
25.11.20233.5 Mб09917.pdf
#
25.11.20233.5 Mб09918.pdf
#
25.11.20233.5 Mб09919.pdf
#
21.11.2023168.07 Кб1992.pdf
#
25.11.20233.5 Mб09920.pdf
#
25.11.20233.5 Mб09921.pdf
#
25.11.20233.5 Mб19922.pdf
#
25.11.20233.5 Mб09923.pdf