
9818
.pdf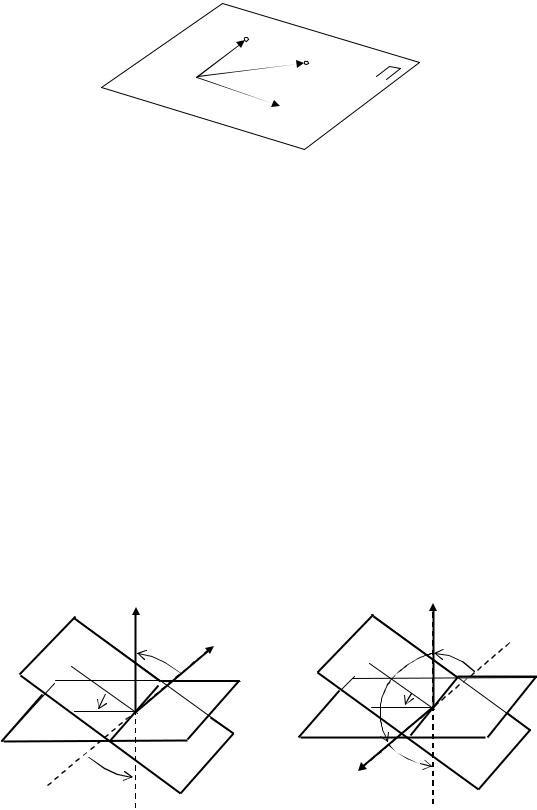
[Введите текст]
Получим уравнение плоскости, проходящей через три заданные точки M1 ( x1, y1, z1 ) , M 2 (x2 , y2 , z2 ) , M 3 (x3 , y3 , z3 ) . Пусть M (x, y, z) – произ-
вольная точка плоскости П .
M2
M
M1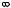
 M3
M3
|
|
Рис. 11.7 |
|
|
Тогда три вектора M1M , M1M2 , |
M1M3 будут компланарными и, следова- |
|||
тельно, их смешанное произведение равно нулю |
|
|||
|
x − x1 |
y − y1 |
z − z1 |
|
|
|
|||
|
x2 − x1 |
y2 − y1 |
z2 − z1 |
= 0 . |
|
x3 − x1 |
y3 − y1 |
z3 − z1 |
|
Раскладывая этот определитель по элементам первой строки, приведем его
клинейному уравнению относительно x, y, z вида (11.2).
11.2.Взаимное расположение двух плоскостей. Пусть заданы две плоскости П1 и П2 уравнениями (см. рис. 11.8).
A1x + B1 y + C1z + D1 = 0 , A2 x + B2 y + C2 z + D2 = 0 .
a ) |
N1 |
|
b) |
|
N1 |
П2 |
ϕ |
N2 |
|
ϕ |
α |
|
|
||||
α |
|
|
|
α |
|
П |
|
|
|
П1 |
|
1 |
|
|
|
|
|
|
α |
|
|
α |
П2 |
|
|
|
|
||
|
|
|
N2 |
|
Рис. 11.8
80

[Введите текст]
Найдем угол между ними в предположении, что они пересекаются. Пересекаясь, плоскости образуют две пары равных двугранных углов. Углом α между плоскостями П1 и П2 будем считать меньший из этих двугранных углов (см. рис. 11.8). Выразим угол α между плоскостями через
угол |
ϕ между нормальными |
к ним векторами |
N1 = { A1 , B1 ,C1} |
и |
|||||||||||
N2 = { A2 , B2 ,C2} . Если угол ϕ острый, то |
α = ϕ (как углы с взаимно пер- |
||||||||||||||
пендикулярными сторонами). Если же угол |
ϕ – |
тупой, то α = π − ϕ (см. |
|||||||||||||
рис. |
11.8 b) ), поэтому |
cos α = − cos ϕ . В итоге |
для вычисления угла |
α |
|||||||||||
между плоскостями имеем формулу |
|
|
|
|
|
|
|
||||||||
|
cos α = |
|< N 1 |
, N 2 |
>| |
= |
|
| A1 A2 + B1B2 + C1C2 | |
|
|||||||
|
|
UUR |
UUR |
|
|
|
|
|
|
|
|
. |
|
||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
| N 1 | |
×| N 2 | |
|
|
A12 + B12 |
+ C12 |
|
A12 + |
B12 + C12 |
|
||||
В частности, условие перпендикулярности и условие параллельности двух плоскостей имеют вид
П1 П2 A1 A2 + B1B2 + С1С2 = 0 ;
П П |
2 |
|
A1 |
= |
B1 |
= |
С1 |
. |
|
|
|
||||||
1 |
|
A2 |
|
B2 |
|
С2 |
||
|
|
|
|
|
||||
В последнем случае, если дополнительно выполняется равенство
A1 |
= |
B1 |
= |
C1 |
= |
D1 |
, |
(11.4) |
|
A2 |
B2 |
C2 |
D2 |
||||||
|
|
|
|
|
то эти плоскости совпадают.
Аналогично понятию пучка прямых на плоскости существует поня-
тие пучка плоскостей, проходящих через линию пересечения двух за-
данных плоскостей. В частности, им удобно пользоваться, когда нужно найти плоскость, проходящую через линию пересечения данных плоскостей и удовлетворяющую некоторому дополнительному условию. Уравнение пучка плоскостей имеет вид
( A1x + B1 y + C1z + D1 ) + λ( A2 x + B2 y + C2 z + D2 ) = 0 . |
(11.5) |
Действительно, уравнение (11.5) – уравнение плоскости. Так как координаты любой точки, принадлежащей линии пересечения П1 и П2 , обращают в ноль обе скобки в (11.5), то при любом λ эта плоскость проходит через линию пересечения этих плоскостей.
81
[Введите текст]
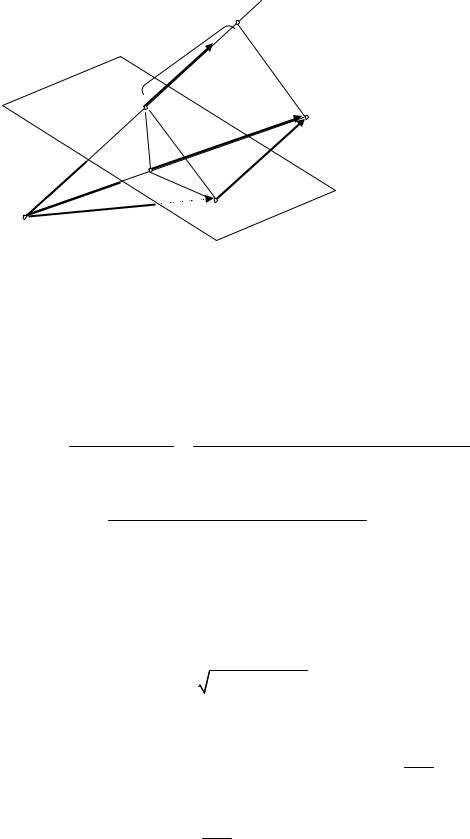
11.3. Расстояние от точки до плоскости. Пусть требуется вычислить расстояние от точки M 0 (x0 , y0 , z0 ) до плоскости Ax + By + Cz + D = 0 .
d
N
M0
|
d |
O |
M 1 |
Рис. 11.9
Пусть M1 (x1, y1, z1 ) – проекция точки M 0 на данную плоскость (см. рис. 11.9). Искомое расстояние равно абсолютной величине проекции век-
тора |
M1M0 |
на направление нормального вектора N = { A, B,C } : |
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
UUUUUUR |
|
|< N ,M |
M |
|
>| |
|
|
|
|
A( x − x ) + B( y |
|
|
− y ) + C( z |
|
− z ) |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
R |
|
|
|
R1 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
1 |
|
|
0R |
1 |
|
|
|
0 |
1 |
|
||||
d = |
|
= |
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
= |
||||||||||||||||||||
ПрN M1M 0 |
|
| N | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| N | |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
= |
|
Ax |
|
+ By |
|
|
+ Cz |
|
|
− Ax |
− By − Cz |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
R |
1 |
1 |
|
|
|
|
1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| N | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Так |
|
как |
точка |
|
M1 (x1, y1, z1 ) |
|
|
|
|
|
|
|
принадлежит |
|
|
плоскости, то |
||||||||||||||||||||||||
Ax1 + By1 + Cz1 = −D , поэтому |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
d = |
|
|
Ax0 |
+ By0 + Cz0 + D |
|
|
. |
|
|
|
|
|
(11.6) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A2 + B2 + C 2 |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Найдём координаты точки |
|
|
M1 (x1, y1, z1 ) . |
Для этого выразим вектор |
||||||||||||||||||||||||||||||||||||
M M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
R |
|
|
0 |
через найденное расстояние |
|
|
d |
и единичный вектор |
R |
N , нор- |
|||||||||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| N | |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
мальный к плоскости |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
UUUUUUR |
= ± |
|
d |
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
(11.7) |
|||||||||||||
|
|
|
|
|
|
|
|
M |
1 |
M |
0 |
|
R |
|
|
N . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
N | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
82 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
[Введите текст] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из формулы (11.6) |
видно, что знак проекции вектора M1M0 определяется |
||||||||||||||||
знаком выражения |
Ax0 + By0 + Cz0 + D , |
т.е., если Ax0 + By0 + Cz0 + D > 0 , |
|||||||||||||||
то M1M 0 −− N , и в формуле (11.7) нужно взять знак «плюс». |
|||||||||||||||||
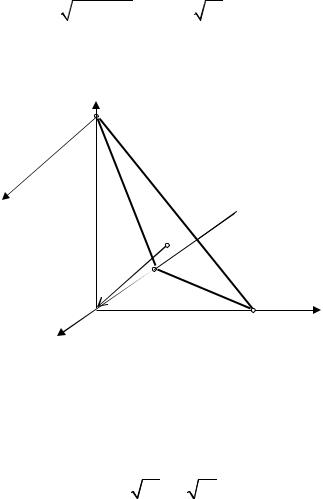
Пример. Найти проекцию начала координат на плоскость |
|||||||||||||||||
|
|
|
|
3x − 2y − z + 7 = 0. |
|||||||||||||
Пусть M1 (x1, y1, z1 ) |
– проекция точки (0,0,0) на данную плоскость (см. |
||||||||||||||||
рис.11.10). Вычисляем расстояние точки |
(0,0,0) до плоскости |
||||||||||||||||
|
d = |
|
|
3 × 0 - 2 × 0 -1× 0 + 7 |
|
|
= |
|
|
|
7 |
|
|
|
»1.9 |
||
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||||||||
|
1 + 4 + 9 |
14 |
|
|
|||||||||||||
Отсюда следует, что M1O = {−x1, − y1,−z1} −− N = {3, −2, −1}
N
M1
d
y
x O 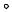
Рис. 11.10
Из равенства (11.7), взятого со знаком плюс, имеем
{−x , − y , −z }= |
|
7 |
|
|
{3, − |
2, −1} |
. |
|||
|
|
|
|
|
|
|||||
|
|
|||||||||
1 |
1 |
1 |
14 |
14 |
|
|
||||
|
|
|
|
|
||||||
Отсюда находим M1 (−1.5,1, 0.5) .
83

[Введите текст]
Лекция 12. Прямая линия в пространстве
12.1. Различные виды уравнений прямой. Пусть в трехмерном про-
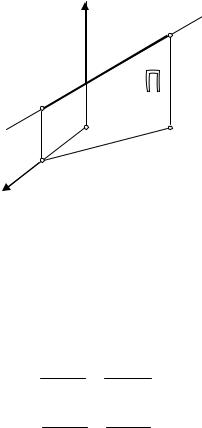
странстве с декартовой прямоугольной системой координат имеем прямую L , и мы хотим получить уравнение, связывающее координаты любой её точки. Пусть M 0 (x0 , y0 , z0 ) – некоторая фиксированная точка этой прямой
и S = {m, n, p} – вектор, параллельный прямой L , называемый направ-
ляющим вектором этой прямой
z
S
M 0
y
r0
r M
x
|
Рис. 12.1 |
|
Возьмем на прямой |
L произвольную точку M (x, y, z) . Рассмотрим |
|
следующие векторы |
M0M = {x − x0 , y − y0 , z − z0}, |
r = {x0 , y0 , z0} и |
r = {x, y, z} . Очевидно, что векторы M0M и S коллинеарны, поэтому су-
ществует число t такое, что M0M = t S , т.е.
R |
R |
= t S . |
|
r |
− r0 |
(12.1) |
Записывая равенство (12.1) в координатах, получим так называемые пара-
метрические уравнения прямой в пространстве
x = x0 |
+ m t |
|
y = y0 + nt |
(12.2) |
|
z = z0 |
+ p t |
|
Ясно, что при изменении значения параметра t в пределах от −∞ до +∞ точка M (x, y, z) «пробегает» всю прямую L . В частности, при t = 0 уравнения (12.2) дают координаты точки M 0 (x0 , y0 , z0 ) .
84
[Введите текст]
Выразим параметр t из каждого уравнения (12.2), приравняем друг другу полученные выражения и придем к так называемым каноническим
уравнениям прямой в пространстве
|
x − x0 |
= |
y − y0 |
= |
z − z0 |
. |
(12.3) |
|||||
|
m |
|
|
|
||||||||
|
|
|
n |
|
|
|
p |
|
||||
Заметим, что на плоскости |
xOy каноническое уравнение прямой, |
прохо- |
||||||||||
дящей через точку M 0 (x0 , y0 ) |
с направляющим вектором S = {m, n}, |
имеет |
||||||||||
вид |
|
|
x − x0 |
|
|
y − y0 |
|
|
|
|||
|
|
|
|
= |
. |
(12.4) |
||||||
|
|
|
|
|
m |
|
||||||
|
|
|
|
|
|
|
|
n |
|
|||
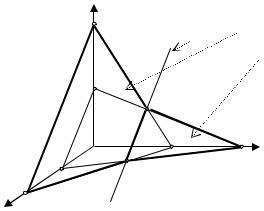
Обратим внимание, что уравнения (12.3) представляют собой краткую запись трёх равенств. Рассмотрим, например, одно из них (12.4). Это уравнение плоскости, параллельной оси O z . Так как координаты любой точки прямой (12.3) удовлетворяют уравнению (12.4), то прямая L лежит в этой плоскости
z
L
y O 
x
Рис.12.2
Линия пересечения плоскости (12.4) с плоскостью xOy является проекцией прямой L на эту координатную плоскость.
Рассматривая совместно пару равенств из (12.3) , например,
x − x0
mx − x0m
= y − y0
n
,
= z − z0 p
получим уравнение прямой L в виде линии пересечения двух плоскостей.
85
[Введите текст]
В общем случае уравнения прямой как линии пересечения двух непараллельных плоскостей П1 и П2 имеют вид
A1 x + B1 y + C1 z + D1 = 0
A2 x + B2 y + C2 z + D2 = 0 (12.5)
Приведём конкретный пример задания прямой в таком виде (см. рис. 2.3).
z |
3 x + 4 y + 2 z − 12 |
= 0 |
|
|
|||
|
L : |
= 0 |
|
|
3 x + y + 2 z − 6 |
||
y
x
Рис. 12.3
Выше был показан переход от канонических уравнений прямой к уравнениям вида (12.5). Покажем, как из уравнений (12.5) получить канонические уравнения этой прямой. Для этого надо найти какую-нибудь одну точку прямой L и её направляющий вектор. Для нахождения координат точки решим систему двух уравнений (12.5) относительно двух переменных, коэффициенты перед которыми образуют базисный минор, фиксируя при этом третью переменную. Совместность этой системы уравнений, а значит, и наличие такого минора, гарантируется предположением о том, что плоско-
сти П1 и П2 не параллельны. |
Пусть, например, |
|
||||||||||||||||||
|
|
|
|
D = |
|
A1 |
B1 |
|
¹ 0 , |
|
|
|
|
|||||||
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
A2 |
B2 |
|
|
|
|
|
|
|
|||
тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
C1z + D1 |
B1 |
|
|
|
|
|
|
A1 |
C1z + D1 |
|
|
|
|
||||
|
|
|
|
|
|
|
||||||||||||||
x = − |
|
|
C2 z + D2 |
B2 |
|
|
, y = − |
|
|
A2 |
C2 z + D2 |
|
|
. |
(12.6) |
|||||
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Раскрывая определители в этих выражениях, представим решения
системы (12.5) в виде
x = αz + β , y = γz + δ .
86

[Введите текст]
Будем рассматривать переменную |
z в качестве параметра, |
||||||
её из полученных равенств и запишем их в виде |
|||||||
|
x − β |
= |
y − δ |
|
= |
z |
. |
|
α |
γ |
|
||||
|
|
1 |
|
||||
выразим
(12.7)
Таким образом, координаты точек прямой L , заданной уравнениями (12.5), удовлетворяют уравнениям (12.7), которые можно рассматривать как канонические уравнения этой прямой. В частности, точка (β,δ,0) лежит на
этой прямой, а S = {α, γ,1} – её направляющий вектор.
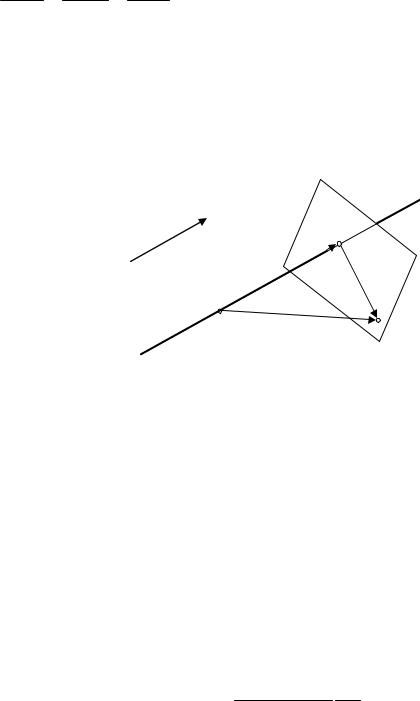
Возможен и другой путь получения канонических уравнений прямой из уравнений прямой как линии пересечения двух плоскостей П1 и П2 , заданных уравнениями (12.5)
N1 П2
N2
|
П1 |
|
|
|
|
|
S |
|
|
|
|
|
|
|
Рис. 12.4 |
|
|
|
|
Очевидно, что в качестве направляющего вектора S = {m, n, p} прямой |
|||||||||
L можно взять векторное произведение векторов |
N1 = {A1, B1,C1} и |
||||||||
N2 = {A2 , B2 ,C2}, т.е. |
|
|
|
R |
R |
|
|
|
|
|
|
|
|
k |
|
|
|
||
|
|
|
|
|
|
|
|||
R |
UUR |
UUR |
|
i |
j |
R |
R |
R |
|
|
|
|
|
||||||
S |
= N1 |
× N2 |
= |
A1 |
B1 |
C1 |
= mi |
+ n j |
+ pk , |
|
|
|
|
A2 |
B2 |
C2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
а координаты какой-нибудь точки этой прямой получим, решая систему (12.5) при фиксированном значении переменной z (например, z = 0 ).
|
Получим уравнения прямой в пространстве, проходящей через две |
|||||
заданные точки M1 (x1, y1, z1 ) |
и M 2 (x2 , y2 , z2 ) . Очевидно, что направляю- |
|||||
щим |
вектором |
этой |
прямой |
может |
служить |
вектор |
M1M2 ={x2 − x1, y2 − y1, z2 − z1}, и тогда канонические уравнения примут вид
87
[Введите текст]
x − x1 |
= |
y − y1 |
= |
z − z1 |
. |
(12.8) |
x2 − x1 |
y2 − y1 |
|
||||
|
|
z2 − z1 |
|
|||
12.2.Проекция точки на прямую и расстояние от точки до прямой
впространстве. Пусть прямая задана каноническими уравнениями
x − x1 = y − y1 = z − z1 .
m |
n |
p |
Обозначим через M 2 (x2 , y2 , z2 ) проекцию точки M 0 на данную пря- |
||
мую (см. рис. 12.5). |
Напомним, что проекцией точки M на ось L в про- |
|
странстве называется точка M1 пересечения оси L и плоскости, проходя- |
||
щей через точку M 0 |
перпендикулярно этой оси. |
|
S |
M 2 |
L |
M 1
M 0
Рис.12.5
Требуется найти координаты точки M 2 и расстояние от точки M 0 (x0 , y0 , z0 ) до этой прямой. Искомая точка будет найдена, если мы найдем
вектор M1M2 , который коллинеарен |
|
вектору S = {m, n, p} и имеет длину, |
|||||||||
равную |
модулю проекции вектора M1M0 = {x0 − x1, y0 − y1, z0 − z1} |
на век- |
|||||||||
тор S . |
Так как |
|
|
|
|
|
|
|
|
|
|
|
|
UUUUUUR |
= |
< M M , S > |
|
|
|||||
|
R |
M1M 0 |
|
|
1 R 0 |
, |
|
||||
|
ПрS |
|
|
| S | |
|
||||||
|
|
|
|
|
|
|
|
|
|||
то |
|
< M |
|
|
|
, S > S |
|
|
|||
|
UUUUUUR |
|
|
M |
|
|
|||||
|
M1M 2 = |
1 |
|
|
|||||||
|
|
R 0 |
|
R |
. |
|
(12.9) |
||||
|
|
|
|
|
|||||||
|
|
|
|
| S | |
|
| S | |
|
|
|||
88
[Введите текст]
Поэтому искомое расстояние вычисляется по формуле
UUUUUUR UUUUUUR |
|
UUUUUUR |
|
< M1M |
0 , S > |
R |
|||||
d =| M1M0 - M1M 2 |
| = | M1M0 |
- |
|
R |
|
× S | . |
|||||
|
| S |2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
||
Пример. Вычислить расстояние точки M 0 (2, −1,3) |
до прямой |
||||||||||
|
x |
= |
y + 7 |
= |
z − 2 |
|
|
|
|||
3 |
|
|
|
|
|
||||||
|
5 |
|
|
2 |
|
|
|
|
|||
и найти её проекцию на эту прямую.
Выберем точку на прямой M1 (0, −7, 2) , тогда M1M0 ={2,6,1}. Вычис-
лим скалярное произведение < M1M0 , S > = 38 , |
квадрат модуля | S |2 = 38 |
|||||
направляющего вектора |
S ={3,5,2}, и по формуле (12.9) |
получим |
||||
M1M 2 ={3,5, 2}: |
|
|
|
|
|
|
d =| 2i + 6 j + k - (3i + 5 j + 2k ) |=| -i + j - k |= |
|
. |
|
|||
3 |
|
|||||
Координаты проекции |
точки |
M 2 (x2 , y2 , z2 ) |
находим из |
равенства |
||
M1M2 ={x2 - 0, y2 + 7, z2 - 2} = M2 (3, -2,4) , поэтому окончательно получаем
M 2 (3, −2, 4) .
В частности, таким способом можно находить расстояние между параллельными прямыми в пространстве как расстояние от точки, взятой на одной прямой, до другой прямой.
12.3. Пересечение прямых в пространстве. Пусть две прямые L1 и
L2 заданы каноническими уравнениями
L : |
x − x1 |
= |
y − y1 |
= |
z − z1 |
, |
L : |
x − x2 |
= |
y − y2 |
= |
z − z2 |
. |
|
|
|
|
|
|
||||||||
1 |
m1 |
|
n1 |
|
p1 |
2 |
m2 |
|
n2 |
|
p2 |
||
|
|
|
|
|
|
||||||||
Выясним условия пересечения этих прямых. Предполагаем, что направ-
ляющие векторы этих прямых S1 ={m1, n1, p1} и S2 ={m2 , n2 , p2} не коллинеарны, что исключает случаи параллельности или совпадения этих прямых, и, кроме того, точки M1 (x1, y1, z1 ) и M 2 (x2 , y2 , z2 ) различные (см.
рис.12.6).
89
