9742

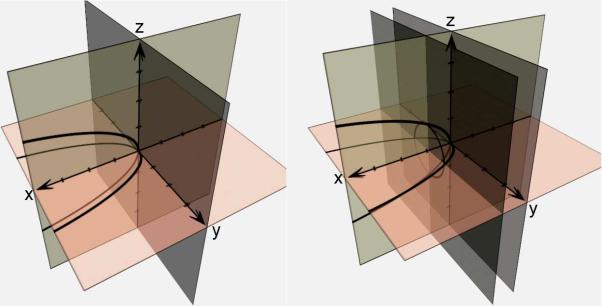
Можно доказать, что через каждую точку однополостного гиперболоида проходит прямая, определяемая системой (8.4). То есть прямые (называемые прямолинейными образующими однополостного гиперболоида) покрывают его поверхность целиком.

Поверхности, составленные из прямых, называют

линейчатыми. Ясно, что конусы и цилиндры относятся к этому классу. Но для однополостного гиперболоида геометрически такое свойство не очевидно. Тем не менее, как мы убедились,

однополостный гиперболоид является линейчатой поверхностью.

Более того, он обладает двумя системами прямолинейных образующих (рис. 8.3).

Вторую систему уравнений прямолинейных образующих однополостного гиперболоида можно получить по аналогии с системой (8.4):

Знаменитый русский инженер Владимир Григорьевич Шухов

(1853 - 1939) использовал в строительной технике возможность образования однополостного гиперболоида прямыми линиями.

Ему принадлежит идея создания металлических конструкций из балок, расположенных по прямолинейным образующим однополостного гиперболоида вращения. Эти конструкции обладают большой жёсткостью, прочностью и малым весом. Они применяются для устройства водонапорных башен и высоких радиомачт.

В 1896 году на Всероссийской промышленной и художественной выставке в Нижнем Новгороде были выставлены

70

сетчатые конструкции, изготовленные по проекту В.Г. Шухова:

павильоны с висячими покрытиями и павильоны с сетчатыми оболочками, а также гиперболоидная водонапорная башня. Это было моментом рождения рациональной архитектуры,

использовавшей новаторские конструктивные формы. В

Нижегородской области сохранились подлинные сооружения

В.Г. Шухова, являющиеся памятниками инженерного искусства мирового уровня.

Рассмотрим далее уравнение двуполостного гиперболоида

поверхности, определяемой этим уравнением, получаются

эллипсы.

Но если рассмотреть сечение координатной плоскостью xOу ,

означает, что поверхность не пересекается с координатной плоскостью xOу , также как со всеми плоскостями z = h при h < c . Следовательно, она состоит из двух отдельных «полостей»,

имеющих вид бесконечных выпуклых чаш (рис. 8.4).

Двуполостный гиперболоид обладает тремя плоскостями симметрии (при данном выборе осей они совпадают с координатными плоскостями). Величины a , b и c называются полуосями двуполостного гиперболоида.

71

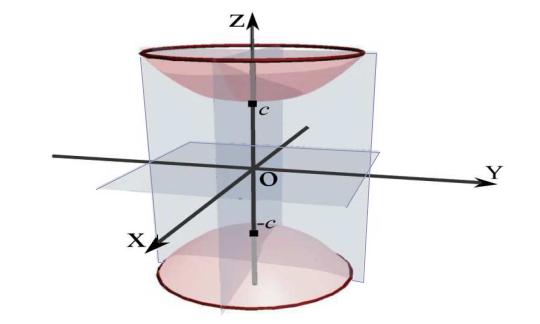
Рис. 8.4

Если a = b, то двуполостный гиперболоид становится поверхностью вращения и может быть получен вращением

Можно получить двуполостный гиперболоид вращения с

Конус

Рассмотрим уравнение конуса второго порядка

поверхности, определяемой этим уравнением, получаются пересекающиеся прямые, а в сечениях, параллельных координатной плоскости xOу - эллипсы (рис. 8.5). Эта поверхность называется конусом.

72

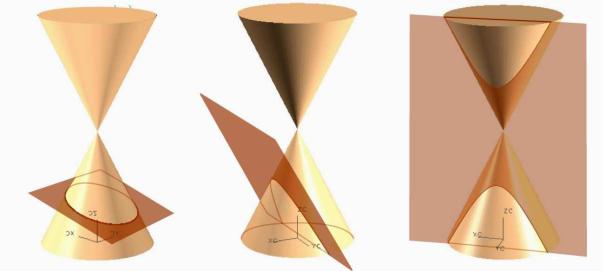
Рис. 8.5

Если a =b, то конус становится поверхностью вращения (в

этом случае он называется круговым конусом) и может быть

прямую закрутить вокруг оси Oy , то получится круговой конус с

Особенностью конуса является то, что любое его сечение плоскостью, не проходящей через вершину, есть эллипс,

гипербола или парабола (в зависимости от наклона секущей плоскости). Поэтому эти классические линии со времён Древней Греции называют коническими сечениями. Часто встречаясь в явлениях природы и деятельности человека, эти линии приобрели особое значение после открытия, сделанного из наблюдений И.Кеплером в 1609 году и теоретически обоснованного И.Ньютоном в 1687 году: планеты и кометы Солнечной системы движутся по коническим сечениям, в одном из фокусов которого находится Солнце.

73

Параболоиды

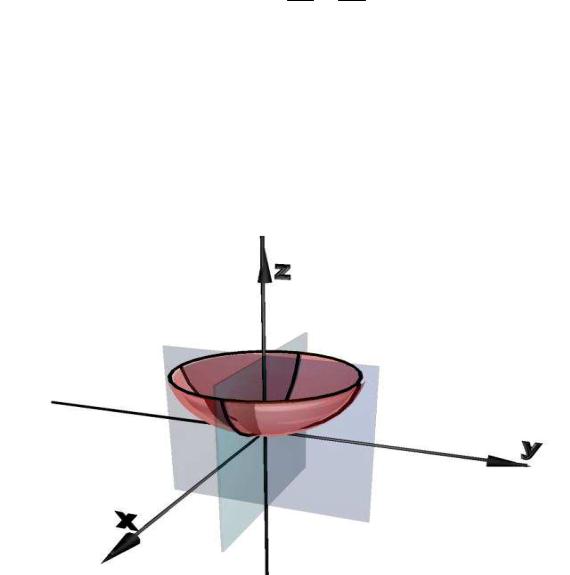
Рассмотрим уравнение эллиптического параболоида

2z = x2 + y2 , p q

где параметры p и q положительны. В сечениях координатными плоскостями xOz и yOz поверхности,

определяемой этим уравнением, получаются параболы, а в сечениях z = h при h > 0 - эллипсы (рис. 8.6).

Рис. 8.6

Эллиптический параболоид обладает двумя плоскостями симметрии (при данном выборе осей они совпадают с координатными плоскостями xOz и yOz ). При p = q параболоид становится поверхностью вращения (в этом случае он называется параболоидом вращения) и может быть получен вращением параболы вокруг своей оси.

74

Рассмотрим уравнение гиперболического параболоида

плоскостью xOz поверхности, определяемой этим уравнением,

«нисходящая» парабола с уравнением y2 = −2qz . Аналогично,

каждая плоскость y = h пересекает поверхность по «восходящей» параболе, а каждая плоскость x = h – по «нисходящей» параболе.

В сечениях, параллельных координатной плоскости xOy ,

получаются гиперболы. Гиперболический параболоид обладает двумя плоскостями симметрии (при данном выборе осей они совпадают с координатными плоскостями xOz и yOz ) и имеет вид «седла» (рис. 8.7).

Рис. 8.7

75

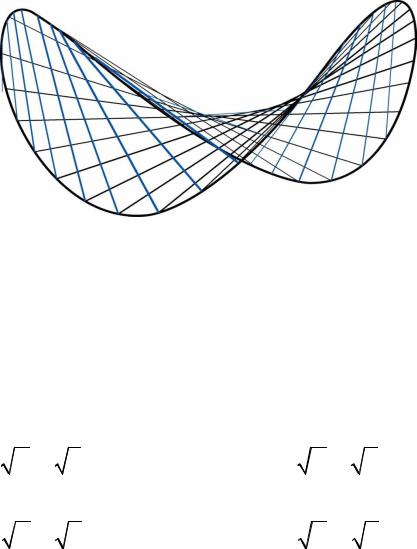
Поверхность гиперболического параболоида можно также

получить «механическим» образом. Пусть одна парабола

нижнюю параболу скользить вершиной по верхней параболе,

перемещаясь параллельно плоскости yOz . Эта скользящая

парабола и образует гиперболический параболоид.

Интересно, что гиперболический параболоид, как и однополостный гиперболоид, является линейчатой поверхностью

– его можно сформировать из прямых (рис. 8.8).

Рис. 8.8

Гиперболический параболоид с уравнением (8.6) имеет две системы прямолинейных образующих, определяемых уравнениями

Завершим обзор поверхностей второго порядка полной их классификацией. Всякое уравнение второго порядка в пространстве с помощью подходящего параллельного переноса и поворота осей координат может быть приведено к одному из видов, соответствующих рассмотренным поверхностям:

2 2

8)2z = p q (гиперболический параболоид)

9)- 17) уравнения кривых второго порядка задают в пространстве девять видов цилиндров второго порядка.− yx

Построение тел, ограниченных

несколькими поверхностями

Наиболее интересные задачи, связанные с разобранными вопросами, - это получение формы тел, ограниченных несколькими поверхностями.

77

Пример. Построить тело, сформированное двумя поверхностями, заданными уравнениями

эллипсоид вращения с полуосями a = 3, b = c = 2 . Его общий вид

изображен на рисунке 7.5. Уравнение (8.8) задаёт параболоид вращения, который, в отличие от изображённого на рисунке 8.6,

симметричен относительно оси Ox . Здесь параболы получаются в сечениях координатными плоскостями xOz и xOy (рис. 8.9), а

в сечениях плоскостями x = h , если h > 0 - окружности (рис. 8.10).

эллипсоида, то его сечение плоскостями x = h , если h > 0 , тоже являются окружностями. Можно найти значение h , при котором

78

радиусы окружностей параболоида и эллипсоида совпадут, то есть поверхности пересекутся. Для этого выразим из (8.8)

решений квадратного уравнения оставляем положительное x = 2 .

Итак, эллипсоид и параболоид пересекутся при x = 2 по

Рис. 8.11

Обе поверхности можно теперь построить в одних координатных осях (рис. 8.12) и изобразить вид тела, ими ограниченного (рис. 8.13).

79