9715

[Введите текст]

Рис. 14.4

Это подсказывает и путь решения задачи: искомая проекция M2 находится как точка пересечения плоскости (14.2) и прямой L .

Задача 5. Написать уравнение плоскости, проходящей через заданную точкуM 0 (x0 , y0 , z0 ) параллельно двум неколлинеарным векторам

a = {a1, a2 , a3} и b = {b1,b2 ,b3}.

2

*

0

Рис. 14.5

Ясно, что в качестве нормального вектора к требуемой плоскости можно взять векторное произведение данных векторов, т.е.

Тогда уравнение искомой плоскости имеет вид

A(x − x0 ) + B( y − y0 ) + C(z − z0 ) = 0 .

100

[Введите текст]

Эту же задачу можно решить и другим способом. Пусть M (x, y, z) –

произвольная точка требуемой плоскости. Тогда три вектора M0M , a, b – компланарны, и уравнение плоскости получается из условия их компланарности, а именно

Задача 6. Составить уравнение пучка плоскостей, проходящих через дан-

в котором λ – некоторый параметр. Действительно, если точка лежит на данной прямой L , то её координаты обращают в ноль оба уравнения, которыми задана прямая, а, значит, удовлетворяют уравнению (14.3) при любом λ. Меняя значения λ, будем получать различные плоскости, проходящие через эту прямую.

Выберем, например, из этого пучка плоскость, перпендикулярную данной плоскости П

Рис. 14.9

Для этого представим уравнение пучка в виде

101

[Введите текст]

Из перпендикулярности плоскостей (14.4) и (14.5) следует, что их нормальные векторы взаимно перпендикулярны, т.е.

( A1 + λA2 ) A3 + ( B1 + λB2 ) B3 + (C1 + λC2 ) C3 = 0 .

Отсюда находим значение λ, соответствующее искомой плоскости.

Задача 7. Написать уравнение плоскости, проходящей через заданную точку M 1 ( x1 , y1 , z1 ) и прямую.

Если прямая задана каноническими уравнениями

L : x − x0 = y − y0 = z − z0 ,

то задача сводится к предыдущей, если в качестве вектора b взять на-

Рис. 14.6

Если же прямая задана как пересечение двух плоскостей

A1 x + B1 y + C1 z + D1 = 0

A2 x + B2 y + C2 z + D2 = 0 ,

то естественнее воспользоваться уравнением пучка плоскостей «порождённых» этой прямой

( A1 x + B1 y + C1 z + D1 ) + λ ( A2 x + B2 y + C2 z + D2 ) = 0 .

102

[Введите текст]

Неизвестное значение λ определяется из условия прохождения одной из плоскостей этого пучка через данную точку (см. рис. 14.7).

( A1 x1 + B1 y1 + C1 z1 + D1 ) + λ ( A2 x1 + B2 y1 + C2 z1 + D2 ) = 0.

Рис. 14.7

Задача 8. Составить уравнение плоскости, проходящей через две параллельные прямые

103

[Введите текст]

Раздел 4. Математический анализ. Дифференциальное исчисление

Лекция 15. Функция

Этот раздел математики изучает функциональные зависимости, которые в окружающем нас мире встречаются на каждом шагу: температура как функция времени, давление как функция высоты и т.д. Так что же такое функция в математическом смысле?

15.1. Функция и способы её задания. Пусть заданы два множества

X и Y произвольной природы. Допустим, что каждому элементу x неко-

соответствия. Множество D называется областью определения функции, а множество всех элементов y , которые соответствуют элементам множества D , называется областью значений этой функции. Будем называть x

извлечения квадратного корня.

Если функция задана на множестве натуральных чисел, то такая функция называется последовательностью и обозначается символом {an}, который указывает элемент an , соответствующий n . Например, функция факториал an = n! = 1× 2 ×K× (n -1) × n каждому натуральному числу n ставит в соответствие число, равное произведению всех натуральных чисел от 1 до n .

104

[Введите текст]

Последовательность кроме задания формулой своего общего члена an может быть задана иначе. Например, указывается несколько её первых членов, а остальные определяются этими заданными членами по тому или иному правилу. Так определяются знаменитые числа Фибоначчи (названные в честь итальянского математика Леонардо Пизанского (1180–1240), которого называли также Фибоначчи (Fibonacci – сокращённое filius Bonacci, т.е. сын Боначчи)

1,1, 2, 3, 5, 8,13, 21,K

Первые два члена этой последовательности a1 = 1, a2 = 1, а каждый следующий определяется как сумма двух предыдущих, т.е.

an+ 2 = an+1 + an .

Функция может быть задана аналитически с помощью одной или нескольких формул, например,

E(π) = 3, хотя никакой формулой не задаются), или соответствие задано в виде таблицы (например, меню в ресторане), или, наконец, функция может быть задана графически. Под графиком функции в декартовой системе координат понимается множество точек (x, f (x)) .

15.2. Обратная функция. Для данной функции введем понятие обратной функции как такого соответствия f −1 из множества Y в множество X , что в результате последовательного выполнения отображений f и f −1 получим тождественное преобразование f −1 ( f ( x)) = x (см. рис. 15.2)

f

x

y

f −1

Рис. 15.2

105

[Введите текст]

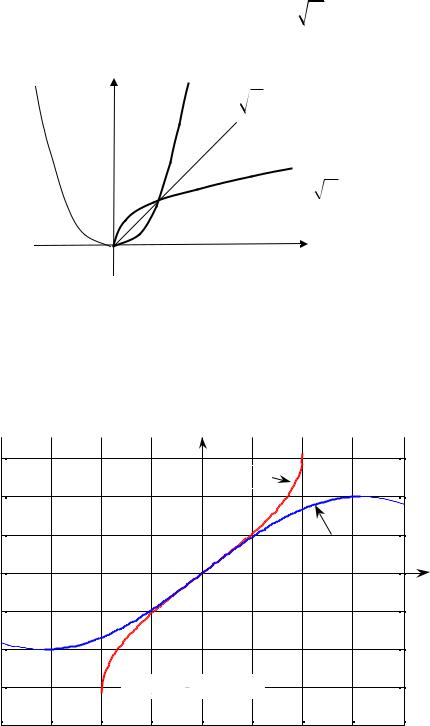
Интуитивно ясно, что не любые функции имеют обратные, а только те, у которых различным элементам x1 ¹ x2 соответствуют различные элементы f (x1 ) ¹ f (x2 ) , т.е. не должно быть ситуации, показанной на рис. 15.1. Если функция не имеет обратной функции во всей области определения, то она может иметь обратную функцию на некотором подмножестве области определения. Так, функция y = x2 не имеет обратной во всей об-

ласти определения, но имеет обратную функциюx = y в области неотри-

цательных чисел (см. рис. 15.3).

x = y

y = x

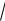y = x

x

Рис. 15.3

Ясно, что график обратной функции, у которой аргументом является y , а значением – x , совпадает с графиком данной функции. Однако при построении графика привычно считать аргументом x , а значением – y .

[Введите текст]

В этом случае график обратной функции окажется симметричным графику исходной функции относительно прямой y = x . В качестве при-

y = arcsin x , ее график представлен на рис. 15.4.

15.3. Предел последовательности. Рассмотрим важное понятие предела функции и введем его сначала для функции натурального аргумента, т.е. для последовательности.

Пределом последовательности { xn } называется конечное число a ,

если для любого сколь угодно малого числа ε > 0 существует такое натуральное число N , что для всех членов последовательности с номерами n > N выполняется неравенство xn − a < ε . В краткой символической за-

писи это выглядит так:

lim xn = a ( ε > 0) ( N ) ( n > N ) (| xn − a |< ε) .

n→∞

Обозначение предела ввёл И. Ньютон в 1686г. Символ lim является сокращением латинского слова limes – граница, граничный камень.

Определим ε -окрестность точки a как множество всех x , удовлетворяющих неравенству x − a < ε, что эквивалентно двойному неравенст-

ву (см. рис. 15.5 )

a − ε < x < a + ε

Тогда понятие предела геометрически означает, что какую бы малую ε -окрестность точки a мы не взяли, найдется такой номер N , начиная с которого все последующие члены последовательности будут находиться в этой окрестности (см. рис.15.5). Последовательность, имеющая конечный предел, называется сходящейся или стремящейся к этому пределу, а неимеющая конечного предела – расходящейся. Часто «стремление» последовательности {xn } к своему пределу a мы будем обозначать более краткой записью xn → a .

107

[Введите текст]

Заметим, что

т.е. последовательность модулей отклонения члена последовательности xn от своего предела a стремится к нулю с увеличением номера n (модуль – лат. modulus – мера).

Примером сходящейся последовательности служит xn = 1/ n . Дейст-

вительно, для любого ε > 0 имеем 1n − 0 < ε , когда n > N = E(1/ ε ). Зна-

чит,

lim 1 = 0 .

n→ ∞ n

Примером расходящейся последовательности служит последовательность xn = (−1)n .

Выше было дано определение предела как некоторого числа, к которому сходится последовательность. Определим так называемые бесконечные пределы. Последовательность называется бесконечно большой, если для любого сколь угодно большого числа M > 0 существует такое нату-

Среди бесконечно больших последовательностей будем различать последовательности, стремящиеся к бесконечности определённого знака.

Дадим в краткой символической форме определения таких последовательностей:

lim xn = + ∞ ( M > 0)( N )( n > N ) (xn > M ) ,

n→∞

lim xn = −∞ ( M > 0)( N) ( n > N)( xn < −M ) .

n→∞

Здесь для краткости употребляется тот же символ lim и слово «пре-

n→∞

дел», хотя следует всегда помнить, что символы + ∞, − ∞ не являются числами, а введены лишь для упрощения записи.

Последовательность, стремящуюся к бесконечности, принято называть бесконечно большой, а последовательность, сходящуюся к нулю, –

бесконечно малой.

108

[Введите текст]

Лекция 16. Свойства пределов. Второй замечательный предел

16.1. Свойства сходящихся последовательностей. Определение предела последовательности не даёт способа его нахождения. Поэтому мы сейчас изучим основные свойства сходящихся последовательностей, которые значительно упростят задачу нахождения пределов.

1. Если последовательность имеет предел, то он единственный.

Действительно, если предположить обратное, т.е. существуют два предела a1 и a2 , и взять непересекающиеся ε -окрестности этих точек (см. рис. 16.1), то, начиная с некоторого номера, все члены последовательности должны одновременно находиться в обеих ε -окрестностях, что невозможно.

2. Сходящаяся к конечному пределу последовательность – огра-

ничена. Это следует из того, что начиная с некоторого N все последующие члены последовательности лежат в ε -окрестности точки a , поэтому | xn |< a + ε n > N , а среди конечного числа первых N членов последовательности, не входящих в эту окрестность, есть наиболее удалённый от

Рис. 16.2

3. В неравенствах для членов двух сходящихся последовательностей можно переходить к пределу, т.е.