
9633
.pdfи потому |
Sn . Но |
при n>2 выполняется неравенство Sn Sn . |
|
Отсюда |
следует, что |
последовательность Sn |
также стремится к |
бесконечности и, следовательно, гармонический ряд расходится. |
|||
При изучении рядов решаются в основном две задачи. Первая задача |
|||
состоит в исследовании |
ряда на сходимость. Вторая задача состоит в |
||
нахождении суммы ряда в случае, если ряд сходится. Вторая задача гораздо сложнее первой, но в некоторых случаях и она поддается решению.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Пример. Найти сумму ряда |
|
|
|
|
|
|
|
|
|
|
, |
если он сходится. |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 n(n 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Так как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n(n 1) |
n |
|
(n 1) |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
то для частичной суммы |
|
Sn |
этого ряда будем иметь: |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
1 |
|
|
1 |
|
|
|
|
1 |
|
... |
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
1 |
|
|
1 |
|
|
1 |
|
||||||||
S n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1 |
2 |
2 3 |
3 |
|
4 |
(n 1)n |
n(n |
1) |
1 |
2 |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
3 |
. |
||||||||||||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
1 |
|
1 |
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
3 |
|
|
4 |
|
|
|
|
n |
1 |
|
|
n |
|
|
n |
|
|
|
(n 1) |
|
|
|
|
n |
1 |
|
|
|||||||||||||||||||
Отсюда следует, что |
|
|
lim Sn 1 lim(1 |
|
1 |
|
|
) 1 |
, |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
n |
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
и, таким образом, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n(n 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
57.2. Простейшие свойства рядов. Непосредственно из элементарных свойств пределов достаточно просто устанавливаются следующие свойства рядов.
1) Сходимость ряда сохранится, если в нем изменить, убрать или добавить конечное число членов.
2) Если все члены ряда uk умножить на число C , то получится
k 1
новый ряд Сuk . Нетрудно видеть, что, если исходный ряд сходится и
k 1
его сумма равна S , то и новый ряд сходится и его сумма равна CS .
|
|
Пусть имеются два ряда uk и |
vk . Суммой (разностью) этих |
k 1 |
k 1 |
|
|
рядов называется ряд (uk vk ) , |
элементы которого получены в |
k 1
результате сложения (вычитания) соответствующих элементов исходных рядов.
Опять-таки из свойств пределов устанавливается следующий факт.
|
|
|
|
3) Если ряды |
uk и |
vk сходятся и их суммы равны |
|
|
k 1 |
k 1 |
|
|
|
|
|
соответственно S1 и |
S2 , то ряд |
(uk |
vk ) также сходится и его сумма |
|
|
k 1 |
|
равна S1 S2 .
Если один из рядов сходится, а другой расходится, то сумма и разность этих рядов будет расходящимся рядом. Если оба ряда расходятся, то никакого общего утверждения о сходимости суммы или разности этих рядов сделать нельзя.
57.3. Признаки сходимости рядов. Рассмотрим ряд признаков,
позволяющих устанавливать сходимость или расходимость ряда. Различают необходимые признаки и достаточные признаки сходимости. Отсутствие необходимого признака позволяет сделать вывод о расходимости ряда. Наличие достаточного признака позволяет сделать вывод о сходимости
ряда.
Наиболее легко проверяемый необходимый признак сходимости ряда состоит в следующем.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если ряд un сходится, |
то |
limun 0. Т.е. в сходящихся рядах |
||||||||||||
n 1 |
|
|
|
n |
|
|
|
|
|
|
|
|
||
общий член обязательно стремиться к нулю. |
|
|
|
|
|
|
|
|||||||
Действительно, можно |
записать, |
что |
un Sn Sn 1 . |
Если ряд (57.1) |
||||||||||
сходится и S его сумма, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim un lim Sn |
lim Sn 1 S S 0 . |
|||||||||||||
n |
n |
|
|
n |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
2n |
|
|
|||
Пример. Исследовать на сходимость ряд |
|
|
. Так как |
|||||||||||
3n 1 |
||||||||||||||
|
|
|
|
|
|
|
|
n 1 |
|
|||||
lim |
2n |
|
lim |
|
2 |
|
|
2 |
|
0 , |
|
|||
|
|
|
|
|
|
|
||||||||
n |
3n 1 |
n 3 1/ n 3 |
|
|
|
|||||||||
то необходимый признак сходимости не выполняется и ряд расходится. Пример с гармоническим рядом показывает, что стремление общего
члена ряда к нулю не является достаточным условием для сходимости
ряда. Действительно, для гармонического ряда lim un |
lim |
1 |
0 . Но |
|
|||
n |
n n |
|
|
ранее было показано, что гармонический ряд расходится.
При изложении достаточных признаков сходимости рядов остановимся сначала на рассмотрении знакоположительных рядов. Такими называются ряды, все члены которых положительны. Рассмотрение
рядов с произвольными по знакам членами отложим до следующего раздела.
Если все члены ряда положительны, то последовательность его частичных сумм монотонно возрастающая и поэтому возможны лишь две ситуации:
1) эта последовательность стремится к бесконечности и ряд является расходящимся;
2) эта последовательность ограничена сверху, а потому имеет предел, и ряд является сходящимся.
Таким образом, для сходимости знакоположительного ряда достаточно доказать ограниченность сверху последовательности его частичных сумм. Именно этот факт гарантируют достаточные признаки сходимости знакоположительных рядов. Наиболее легко проверяемыми из них являются следующие:
почленный признак сравнения;
предельный признак сравнения;
признак Даламбера;
радикальный признак Коши;
интегральный признак Коши.
Остановимся |
на |
рассмотрении |
каждого |
из |
перечисленных |
||||
признаков. |
|
|
|
|
|
|
|
|
|
Почленный признак |
сравнения. |
Пусть |
|
имеются |
два |
||||
знакоположительных ряда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(u) : un , v) : vn |
||||
|
|
|
|
|
|
n 1 |
n 1 |
||
и пусть, начиная с некоторого натурального числа |
N , для |
всех n |
|||||||
справедливо неравенство un vn . Тогда, если ряд |
(v) |
сходится, то ряд |
|||||||
(u) также сходится, |
если |
же |
ряд (u) |
расходится, |
то и |
ряд |
(v) |
||
расходится.
Действительно, так как удаление конечного числа членов ряда не
влияет |
на его сходимость, |
то |
можно считать, |
что |
N 1. Пусть |
||
|
|
|
|
|
|
|
|
S1, S2 ,...,Sn ,...и S1, S2 ,..., Sn ,... частичные суммы ряда (v). Очевидно, что |
|||||||
справедливо неравенство |
Sn |
Sn . |
Поэтому из сходимости ряда (v) |
||||
следует |
ограниченность |
последовательности Sn |
и, |
следовательно, |
|||
сходимость ряда (u) . Если ряд (u) расходится, то последовательность Sn , а, следовательно, и последовательность Sn неограничены, а потому ряд
(v) расходится.
Пример. Исследовать на сходимость ряд
1 |
1 |
|
1 ... |
1 ... |
||||
|
|
|
|
|
|
|
|
|
n 2 ln n |
|
ln 2 |
|
ln 3 |
ln n |
|||

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
||||||
Так как при |
|
n 2 верно, |
что |
|
|
|
|
|
|
|
|
|
|
|
, |
|
а гармонический ряд |
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
ln n |
|
n |
|
n |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
||||||||||||
расходится, то расходится и исследуемый ряд. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
Пример. Исследовать на сходимость ряд |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
... |
..... |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
n 1 |
n |
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Так как |
1 |
|
|
|
1 |
|
, а ряд |
|
|
|
|
|
|
1 |
|
|
|
|
|
сходится, то и исследуемый ряд |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
(n 1) |
2 |
n(n 1) |
n(n 1) |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
сходится. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Предельный признак сравнения. Пусть имеются два |
|||||||||||||||||||||||||||||||||||||||||||||||||
знакоположительных ряда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(u) : un , v) : vn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
и пусть существует lim un |
|
A 0 , |
тогда или оба ряда сходятся, или |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
n v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
оба ряда расходятся. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Доказательство. Пусть ε 0 и такое, |
что A ε 0. Тогда найдется целое |
||||||||||||||||||||||||||||||||||||||||||||||||
положительное N , начиная с которого будет выполняться неравенство |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
A ε |
un |
|
A ε |
или |
|
( A ε)v |
|
u |
|
|
( A ε)v . |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
n |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
vn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Из почленного признака сравнения следует, что, если ряд (u) |
сходится, |
|||||||||||||||||||||||||||||||||||||||||||||||||
то сходится ряд (A ε)(v) , если же ряд (u) |
|
|
расходится, |
то расходится ряд |
||||||||||||||||||||||||||||||||||||||||||||||
(A ε)(v) . Но сходимость |
|
или |
|
|
расходимость |
рядов |
|
(A ε)(v) , (A ε)(v) |
||||||||||||||||||||||||||||||||||||||||||
означает сходимость или расходимость ряда (v). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
При |
применении признаков |
|
сравнения |
|
|
полезно |
|
использовать |
в |
||||||||||||||||||||||||||||||||||||||||
качестве эталонных обобщенные гармонические ряды. Это ряды вида |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
... |
|
|
|
... , |
|
|
|
|
(57.7) |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
k |
k |
|
|
|
|
k |
|
|
k |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
n 1 |
n |
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
где |
k есть постоянное положительное число. |
|
При |
k 1 данный ряд |
||||||||||||||||||||||||||||||||||||||||||||||
совпадает с гармоническим рядом. |
|
Относительно таких рядов справедлив |
||||||||||||||||||||||||||||||||||||||||||||||||
следующий факт (который далее будет доказан): при |
|
k 1 ряд (57.7) |
||||||||||||||||||||||||||||||||||||||||||||||||
сходится, а при k 1 ряд (57.7) расходится. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
Из этого факта следует, например, что обобщенный гармонический |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
||
ряд |
|
|
|
сходится, а |
обобщенный |
|
гармонический |
|
ряд |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
3 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
3 |
|
|
|
2 |
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
n 1 |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
n |
|||||
расходится. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 5 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Пример. Исследовать на сходимость ряд |
|
(u) : |
|
|
|
|
|
. |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
5n |
6 |
n 1 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||

В числителе общего члена данного ряда стоит многочлен 1-ой степени относительно n, а знаменатель при больших n ведет себя, как многочлен третьей степени от n. Поэтому в качестве ряда сравнения берем
|
1 |
|
|
обобщенный гармонический ряд (v): |
с показателем k=2 (равным |
||
2 |
|||
n 1 |
n |
|
|
|
|
разности между степенью многочлена в знаменателе и степенью многочлена в числителе). Найдем
lim |
un |
lim |
|
(n 5)n2 |
|||
|
|
|
|
|
|
||
n vn |
n 5n6 |
n 1 . |
|||||
Если теперь числитель и знаменатель разделить на n3 , то будем иметь
lim un lim |
|
1 5 / п |
|
|
|
1 |
|
0 |
||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
5 |
||||||||
n v |
n |
5 1/ n |
5 |
1/ n |
6 |
|
|
|
|
|||
n |
|
|
|
|
|
|
|
|
|
|
||
Таким образом, предел отношения общих членов этих рядов стремится к пределу, отличному от нуля. А так как ряд ( ) сходится, то и ряд (u)
сходится.
Признак Даламбера. (Жан Даламбер (1717 – 1783) – французский
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
математик). Пусть дан ряд |
|
un с положительными членами и пусть |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
существует |
lim |
un 1 |
q . Тогда: если q 1, то ряд сходится; если q 1, |
|||||||||||||||||||
|
n |
|
un |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
то ряд расходится; если q 1, то ничего определенного сказать нельзя |
||||||||||||||||||||||
(нужны другие методы исследования). |
|
|
|
|
|
|
|
|
||||||||||||||
Доказательство. Пусть |
|
q 1 и пусть ε 0 и такое, |
что q ε 1. Тогда |
|||||||||||||||||||
найдется целое положительное N , |
начиная с которого будет выполняться |
|||||||||||||||||||||
неравенство |
q ε |
un 1 |
q ε , |
|
|
или |
un 1 (q ε)un |
q1un (здесь |
||||||||||||||
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
un |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q1 q ε 1). |
Не теряя общности, можно считать, |
что |
N 1. Тогда будем |
|||||||||||||||||||
иметь |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
2 |
u q |
, |
u |
3 |
u |
q |
1 |
u q2 , ... ,u |
n 1 |
u |
q |
1 |
u qn ,..... |
|||||||
|
|
|
|
|
1 1 |
|
|
|
2 |
|
1 1 |
|
|
n |
|
|
1 1 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Это означает, что члены исследуемого ряда меньше членов ряда u1q1n . |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
Но последний ряд |
представляет |
собой |
сумму |
членов |
геометрической |
|||||||||||||||||
прогрессии со знаменателем |
q1 1 |
|
и потому является сходящимся. По |
|||||||||||||||||||
признаку сравнения таковым является и исследуемый ряд. Аналогично доказывается и случай, когда q 1.
Признак Даламбера можно применять в тех случаях, когда переменная n в записи общего члена ряда стоит или в показателе степени, или вместе со знаком факториала.
Пример. Исследовать на сходимость ряд |
|
n! |
|
|
(u) : |
. |
|||
n |
||||
|
n 1 |
n |
||
Применяя признак Даламбера, имеем: |
|
|
|
|
|
un 1 |
(n 1)!nn |
|
(n 1)nn |
|
nn |
|
1 |
|
1 |
|
|||||
|
un |
|
(n 1)n 1 n! |
|
(n 1)n 1 |
|
(n 1)n |
|
(1 1/ n)n |
n |
e |
. |
||||
(Здесь мы вспомнили второй замечательный предел). |
Т.к. |
|
1 |
|
|
1 то |
||||||||||
|
e |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
исследуемый ряд сходится. |
|
|
|
|
|
|
|
|
|
|
|
|
||||
В тех случаях, когда переменная n в записи общего члена ряда стоит в показателе степени, можно для исследования сходимости применять также радикальный признак Коши, доказательство которого похоже на доказательство признака Даламбера.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Признак Коши |
(радикальный). |
Пусть |
дан |
|
ряд un |
с |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
положительными членами и пусть |
|
существует |
lim n |
un |
|
|
q . Тогда: если |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|||
q 1, то ряд сходится; если q 1, то ряд расходится; если |
q 1, то ничего |
|||||||||||||||||||||||
определенного сказать нельзя (нужны другие методы исследования). |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
При применении признака Коши полезно помнить, что lim n n 1. |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
||
Более того, если Pk (n) есть многочлен степени k относительно n , с |
|
|||||||||||||||||||||||
положительным коэффициентом при старшей степени, то |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
lim n P (n) 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
n |
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n2 |
|
|||||
Пример. Исследовать на сходимость ряд (u) : |
2 |
n . Имеем: |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
n2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
( n n )2 |
|
1 |
|
|
|
|
|
|
|||||||||||
|
un lim n |
|
|
|
|
|
|
|
||||||||||||||||
lim n |
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
1. |
|
|||||||
2 |
|
|
2 |
|
|
2 |
|
|
||||||||||||||||
n |
|
n |
n |
n |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Поэтому исследуемый ряд сходится. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Интегральный признак Коши. |
Пусть |
|
дан ряд |
|
(u) : un |
с |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
||
положительными членами и пусть непрерывная, |
убывающая на участке |
|||
[1; ) функция y f (x) такова, |
что f(n)=un. Тогда, |
если |
несобственный |
|
|
|
|
|
|
интеграл f (x)dx сходится |
(расходится), |
то |
и ряд |
(u) сходится |
1 |
|
|
|
|
(расходится).
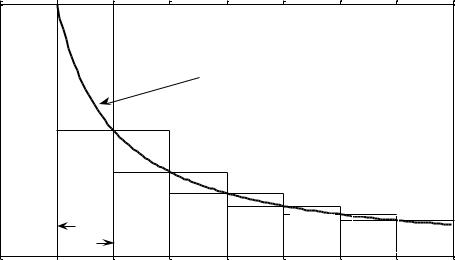
Рассмотрим |
рис. |
57.2. |
Cравнив площади «выступающей» из |
||||||||||||
криволинейной трапеции ступенчатой фигуры и аналогичной фигуры, в ней |
|||||||||||||||
содержащейся, мы получаем неравенства |
|
|
|
|
|
|
|
||||||||
Sn u1 u2 u3 |
... un Jn |
u1 u2 ... un 1 Sn |
un , |
(57.8) |
|||||||||||
где интеграл |
Jn n |
f (x)dx равен значению площади под кривой |
y f (x) |
||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в промежутке [1,n]. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пусть несобственный интеграл сходится, т.е. существует предел |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim J |
n |
J lim |
|
f (x)dx . |
|
|
||||||
|
|
|
n |
|
n |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
Из левой части неравенства (57.8) |
следует |
J n un |
J u1 |
. |
|
||||||||||
|
|
|
|
|
|
y=f(x), f(n)=un |
|
|
|
||||||
|
|
u1 |
u2 |
|
u3 |
|
|
|
|
|
un-2 |
un-1 |
|
|
|
|
|
u2 |
u3 |
|
u4 |
|
|
|
|
|
un-1 |
un |
|
|
|
0 |
1 |
|
2 |
|
3 |
|
4 |
|
|
|
... |
n-1 |
n |
|
|
|
|
|
|
|
|
Рис. 57.2 |
|
|
|
|
|
|
|||
Значит, последовательность Sn |
частичных сумм ряда ограничена сверху и |
||||||||||||||
возрастает, |
т.е. существует |
предел |
lim S |
n |
S . |
Итак, |
из сходимости |
||||||||
|
|
|
|
|
|
|
n |
|
|
|
|
|
|||
интеграла следует сходимость ряда. |
|
|
|
|
|
|
|
|
|
||||||
Пусть теперь несобственный интеграл расходится, т.е. |
|
|
|||||||||||||
|
|
|
n |
|
lim J |
n |
lim |
|
f (x)dx . |
n |
n |
|
||
|
|
|
1 |
|
Тогда правая часть неравенства |
|
(57.8) |
|
показывает, что Sn J n un , т.е. |
частичные суммы ряда не ограничены и, следовательно, ряд расходится.

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
. |
|
|||
Рассмотрим |
обобщенный |
гармонический |
ряд |
Нетрудно |
|||||||||||||||||
|
|
k |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
n |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
видеть, что функция (x) 1 |
xk |
при k 0 |
удовлетворяет перечисленным |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
||||||
выше требованиям. Рассмотрим несобственный интеграл |
|
|
|
при k 1 |
|||||||||||||||||
x |
k |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
dx |
b |
dx |
|
|
x1 k |
|
b |
|
|
b1 k |
|
1 |
|
||||||||
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
||||||||||||||||
|
k |
lim |
|
k lim |
|
|
|
|
lim |
|
|
|
|
|
|
. |
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
1 x |
|
b 1 |
x |
|
b |
1 k |
|
1 |
b |
1 k |
|
1 k |
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
Если k 1, |
то первое |
слагаемое |
|
при |
b |
|
стремится к |
||||||||||||||
бесконечности и, следовательно, несобственный интеграл и, вместе с ним, исследуемый ряд расходится.
Если же k 1, то первое слагаемое при b стремится к 0 и, следовательно, несобственный интеграл сходится к числу 1 (k 1) , а, значит, исследуемый ряд сходится. Таким образом, мы получили те выводы относительно сходимости обобщенных гармонических рядов, которые были декларированы ранее.
Лекция 58. Знакопеременные ряды
58.1. Знакопеременные ряды. Далее будем рассматривать ряды, члены которых могут быть как положительными, так и отрицательными. Прежде всего, остановимся на знакочередующихся рядах. Для удобства будем предполагать, что первый член знакочередующегося ряда положителен. Тогда такой ряд можно записать в виде
|
|
|
|
( 1)n 1un u1 |
u2 |
u3 u4 ... ( 1)n 1un |
... (58.1) |
n 1 |
|
|
|
Для таких рядов при выполнении некоторого дополнительного условия необходимый признак сходимости ряда оказывается и достаточным. Об этом говорит следующая теорема.
Признак Лейбница. Если в знакочередующемся ряде ( 1)n 1un
n 1
члены u монотонно убывают и |
lim u |
n |
0 , |
то ряд сходится и его сумма |
n |
n |
|
|
|
|
|
|
|
|
S удовлетворяет неравенству | S | | u1 | . |
|
|||
Действительно. Пусть Sn сумма первых |
n членов ряда (58.1). Если |
|||
n = 2k, то, с одной стороны, можно записать, что |
||||
S2 k (u1 u2 ) (u3 u4 ) .... (u2 k 1 u2 k ). |
||||
С другой стороны, можно записать, что |
|
|
||
S2k u1 (u2 u3 ) (u4 |
u5 ) .... (u2k 2 u2 k 1 ) u2 k u1 . |
|||
Если n = 2k+1, то, с одной стороны, можно записать, что |
||||
S2k 1 (u1 u2 ) (u3 |
u4 ) .... (u2k 1 u2 k ) u2k 1 . |
|||
С другой стороны, можно записать, что
S2k 1 u1 (u2 u3 ) (u4 u5 ) .... (u2 k 2 u2 k 1 ) (u2 k u2 k 1 ) u1.
Ввиду того, что члены ряда монотонно убывают, эти соотношения показывают, что обе последовательности S2k и S2k 1 , с одной стороны,
монотонно возрастают, а, с другой стороны, обе они ограничены числом u1. Следовательно, эти последовательности имеют пределы S´ и S´´. Но т.к.
lim un 0 |
и |
S2k 1 |
S2k u2k 1 , то S´ =S´´. Отсюда следуют утверждения |
n |
|
|
|
теоремы. |
|
|
|
Вторая |
часть |
утверждения, содержащегося в признаке Лейбница, |
|
очень существенна, ибо она, в случае сходимости ряда, позволяет оценивать
разность между S и Sn , |
где Sn есть сумма первых n членов данного ряда. |
||||||||||||||||||||||||
Действительно, пусть |
есть сумма всех членов ряда, начиная с (n+1)-го. |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
По признаку Лейбница |
|
Rn |
|
un 1 . Но очевидно, что S |
Sn |
Rn или |
|||||||||||||||||||
|
|
||||||||||||||||||||||||
|
S - Sn |
|
|
|
Rn |
|
. Таким образом, |
|
S - Sn |
|
un 1 . |
Иначе говоря, |
сохранив |
||||||||||||
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||
только сумму |
первых |
|
n |
|
|
членов, |
|
мы |
совершаем |
ошибку, не |
|||||||||||||||
превосходящую по модулю модуля первого отброшенного члена. |
|||||||||||||||||||||||||
|
Пример. Исследовать на сходимость ряд |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
n 1 1 |
|
|
|
1 |
|
1 |
|
|
|
n 1 1 |
|
|
|
||||||||
|
|
|
( 1) |
1 |
|
... ( 1) |
... |
(58.2) |
|||||||||||||||||
|
|
|
|
n |
2 |
3 |
|
n |
|||||||||||||||||
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||

Так как последовательность un 1n , монотонно убывая, стремится к 0,
то данный ряд по признаку Лейбница сходится, и из вышесказанного
следует, что |
|
S Sn |
|
|
1 |
|
. |
|
|
||||||
|
|
|
|
||||
|
|
n 1 |
|||||
|
|
|
|
|
|
||
58.2. Абсолютная и условная сходимость рядов. Как подходить к анализу рядов на сходимость в случаях, когда никакой закономерности в чередовании положительных и отрицательных членов в числовом ряде не наблюдаются? В таких случаях может оказаться полезным рассматривать ряды, составленные из абсолютных членов исследуемого ряда.
Пусть дан ряд
u1 u2 ... un ... un (58.3)
n 1
с произвольными по знакам членами. Наряду с ним рассмотрим ряд, составленный из абсолютных величин его членов, т. е. ряд
| u1 | | u2 | ... | un | ... | un | . |
(58.4) |
|
|
n 1 |
|
С точки зрения сходимости этих двух рядов оказывается справедливым следующий факт.
Если ряд (58.4) сходится, то ряд (58.3) также сходится. В этом случае ряд (58.3) называется абсолютно сходящимся рядом.
Если ряд (58.4) расходится, то ряд (58.3) может сходиться, а может расходиться. В тех случаях, когда ряд (58.3) сходится, а ряд (58.4) расходится, ряд (58.3) называется условно сходящимся рядом.
Рассмотренный выше ряд (58.2) является условно сходящимся, так как по признаку Лейбница он сходится, но ряд, составленный из его абсолютных величин, является гармоническим рядом, который (как уже много раз повторялось) расходится. Рассмотрим ряд
( |
1 |
|
1 |
) ( |
1 |
|
|
|
1 |
|
) ( |
|
1 |
|
|
|
1 |
) ( |
1 |
|
|
1 |
) ( |
1 |
|
|
|
1 |
) ( |
1 |
|
|
1 |
) ... |
||||||||||||||||||||||
2 |
2 |
2 |
|
2 |
|
|
2 |
|
2 |
2 |
2 |
2 |
2 |
2 |
2 |
|||||||||||||||||||||||||||||||||||||||||
1 |
|
2 |
|
|
|
3 |
|
|
4 |
|
|
5 |
|
6 |
|
7 |
|
|
|
8 |
|
|
|
9 |
|
|
10 |
|
|
11 |
|
|
|
12 |
|
|
||||||||||||||||||||
Ряд, составленный из абсолютных величин его членов |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
1 |
|
|
|
1 |
|
1 |
|
|
|
1 |
|
|
1 |
|
1 |
|
|
1 |
|
|
1 |
|
|
|
|
1 |
|
|
1 |
|
|
|
1 |
... |
||||||||||||||||
|
|
|
|
2 |
2 |
|
2 |
2 |
|
2 |
|
2 |
2 |
2 |
2 |
|
|
2 |
2 |
|
2 |
|||||||||||||||||||||||||||||||||||
|
|
|
1 |
|
2 |
|
|
3 |
|
|
4 |
|
|
|
|
5 |
|
|
|
|
6 |
|
|
7 |
|
8 |
|
9 |
|
|
10 |
|
|
11 |
|
|
12 |
|
|
|||||||||||||||||
является обобщенным гармоническим рядом с показателем k =2, и
потому он сходится. Следовательно, рассматриваемый ряд сходится
абсолютно.
Принципиальную разницу между абсолютно сходящимися и условно сходящимися рядами дает следующая теорема.
Теорема. При любой перестановке членов абсолютно сходящегося
ряда (при этом можно переставлять как конечное, так и бесконечное число
