
9400
.pdf46.1. Метод неопределенных коэффициентов. Перейдем к нахождению частного решения неоднородного дифференциального уравнения
|
|
|
y′′ + a1 y′ + a2 y = |
f (x) , |
(46.1) |
|||||
когда правая часть |
f (x) |
имеет специальный вид |
|
|||||||
f ( x) = P ( x)eα x |
cosβx |
|
или |
|
|
f ( x) = P ( x)eα x sin βx , |
|
|||
|
n |
|
|
|
|
|
|
n |
|
|
где P (x) = p |
xn + p xn−1 + K + p |
n−1 |
x + p |
n |
– |
заданный многочлен степени n . |
||||
n |
0 |
1 |
|
|
|
|
|
|
||
Характеристикой |
правой |
части |
уравнения (46.1) |
назовем |
||||||
комплексное число α + iβ. Рассмотрим для начала случай действительной характеристики, т.е. когда правая часть имеет вид
f (x) = Р ( x)eαx . |
(46.2) |
n |
|
Будем искать решение в таком же виде, что и правая часть уравнения, т.е.
|
(x) = Q (x)eαx = ( A xn + A xn−1 |
+ K + A |
x + A )eαx |
(46.3) |
||
y |
||||||
|
n |
0 |
1 |
n−1 |
n |
|
где Qn (x) – многочлен, коэффициенты которого подлежат определению
(отсюда происходит и название метода – метод неопределённых коэффициентов). Искомое решение (46.3) должно удовлетворять уравнению с заданной правой частью. Выполнив соответствующую
подстановку |
|
(x) |
в уравнение |
|
(46.1), |
получим |
равенство двух |
||
y |
|
||||||||
многочленов |
|
|
|
|
|
|
|||
′′ |
′ |
2 |
|
|
|
|
|||
Qn (x) + (2α + a1 )Qn ( x) + (α |
+ a1α + a2 )Qn (x) = Pn |
(x) . |
(46.4) |
||||||
|
|||||||||
Справа находится многочлен Pn ( x) |
степени |
n с заданными |
коэффици- |
||||||
ентами. Успех в нахождении коэффициентов многочлена |
Qn (x) зависит от |
||||||||
соотношения между характеристикой правой части α и корнями характеристического уравнения
λ 2+ a1λ + a2 = 0.
∙ Пусть α не совпадает с корнями характеристического уравнения. Тогда в равенстве (46.4) слева многочлен тоже степени n , как и справа. Приравнивая коэффициенты при одинаковых степенях, получим систему
41
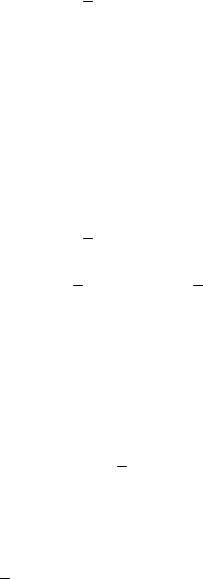
n + 1 |
уравнений |
для нахождения n + 1 |
неизвестных коэффициентов |
A0 , A1 , K, An . |
|
|
|
∙ |
Если α |
простой (однократный) |
корень характеристического |
уравнения, то в левой части равенства (46.4) будет многочлен степени n −1. В этом случае умножим искомый многочлен на x . Степень многочлена увеличится, а число неизвестных коэффициентов не изменится. Задача свелась к предыдущей.
∙ И, наконец, если характеристика α совпадёт с двукратным корнем характеристического уравнения, то искомый многочлен умножаем на x2 .
Итак, если правая часть неоднородного уравнения имеет вид (46.2), то его частное решение отыскиваем в виде
y ( x) = xmQn ( x)eαx ,
где m = 0,1, 2 число совпадений корней характеристического уравнения с характеристикой правой части α , а Qn (x) – многочлен степени n с неопределёнными коэффициентами, которые определяются подстановкой
|
|
(x) в уравнение. |
|
|
|
y |
|
|
|
|
|
Пример. Найти частное решение уравнения y′′ − 3 y′ = x . |
|
|
|
|
Корни характеристического |
уравнения равны λ1 = 0 и |
λ2 = 3 , а |
характеристика правой части – |
α = 0 . Следовательно, m = 1 |
и частное |
||
решение ищем в виде
y (x) = x( A1x + A2 ) .
Найдем
y′ = 2 A1x + A2 , y′′ = 2 A1
и подставив в уравнение, получим тождество
−6 A1x + (2 A1 − 3A2 ) ≡ x .
Приравнивая теперь коэффициенты многочленов справа и слева, получим A1 = −1/ 6 , A2 = 1/ 9 и в результате
y (x) = −(1/ 6)x2 + (1/ 9) x .
В случае комплексной характеристики частное решение неоднородного уравнения ищем в виде
y ( x) = xmeα x (Qn ( x) cos βx + Rn (x) sin βx) ,
где m – число |
совпадений корней |
характеристического |
уравнения с |
характеристикой |
правой части α + βi , |
а Qn (x) и Rn (x) – |
многочлены |
|
42 |
|
|

степени n , коэффициенты которых подлежат определению. Заметим, что в решение входит «полный» тригонометрический многочлен, содержащий как синус, так и косинус, и что перед каждой тригонометрической функцией в качестве множителя находится «свой» многочлен.
В заключение этого раздела подчеркнем, что если правая часть уравнения (46.1) представляет собой сумму двух функций
|
|
f (x) = f1 (x) + f2 (x) , |
||||
то следует найти |
частные |
решения |
|
|
|
|
y1 ( x) и y2 (x) уравнения (46.1) с |
||||||
правыми частями |
f1 ( x) и |
f2 (x) , соответственно. Тогда частное решение |
||||
исходного уравнения (46.1) |
равно сумме этих частных решений |
|||||
y (x) = y1 (x) + y2 (x) .
Это легко проверяется подстановкой y (x) в уравнение
( y1 + y2 )′′ + a1 ( y1 + y2 )′ + a2 ( y1 + y2 ) =
=y1′′ + a1 y1′ + a2 y1 + y2′′ + a1 y2′ + a2 y2 = f1 + f2 .
46.2.Метод вариаций произвольных постоянных – это метод
нахождения частного решения |
|
(x) линейного неоднородного |
y |
дифференциального уравнения второго порядка с постоянными коэффициентами
y′′ + a1 y′ + a2 y = f (x)
с помощью известного общего решения однородного уравнения
y′′ + a1 y′ + a2 y = 0 .
Если метод неопределённых коэффициентов применим для правых частей, имеющих специальный вид, то рассматриваемый метод является
общим. В соответствии с ним частное решение |
|
|
(x) будем |
искать |
||
|
y |
|||||
«похожим» на решение однородного уравнения |
|
|
|
|
|
|
|
y0 (x) = C1 y1 (x) + C2 y2 (x) , |
|
|
|||
где y1(x) и y2 (x) – |
два каких-либо линейно |
независимых |
решения |
|||
соответствующего однородного уравнения, а вместо постоянных |
C1 |
и C2 |
||||
стоят функции u1 (x) и |
u2 (x) , т.е. в виде |
|
|
|
|
|
|
43 |
|
|
|
|
|

y (x) = u1 (x) y1 (x) + u2 (x) y2 (x) .
Задача состоит в нахождении этих функций. Отсюда название – метод вариаций постоянных (постоянные варьируются, изменяются). В дальнейшем, для краткости будем опускать аргументы функций.
Вычисляем производную
|
′ |
( x ) = u |
′ |
+ u |
′ |
+ u |
′ |
|
|||||||
y |
1 y1 |
1 y1 |
2 |
||||
Перед вычислением второй производной, чтобы
′ |
′ |
= 0 . |
u1 y1 |
+ u2 y2 |
y 2 + u 2 y 2′ .
потребуем дополнительно,
(46.5)
Далее мы увидим, что это ограничение поможет нам найти требуемые функции. Тогда
|
|
|
|
|
|
|
|
′ |
|
|
|
′ |
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
y (x) = u1 y1 |
+ u2 y2 |
|
|
|
||||||
и |
|
|
|
′′ |
|
|
|
|
′ |
′ |
|
|
′′ |
′ ′ |
′′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
y (x) = u1 y1 + u1 y1 |
+ u2 y2 |
+ u2 y2 . |
|
|
||||||||||
Подставляя в уравнение |
|
′′ + a1 |
|
+ a2 |
|
= f (x) |
и группируя |
слагаемые, |
|||||||||
y |
y |
y |
|||||||||||||||
получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′′ |
′ |
+ a2 y1 ) + u2 |
′′ |
|
|
|
′ |
′ ′ |
′ ′ |
= f (x) . |
|||||||
u1 ( y1 |
+ a1 y1 |
( y2 |
+ a1 y2 + a2 y2 ) + u1 y1 |
+ u2 y2 |
|||||||||||||
Отсюда, наряду с условием (46.5), получаем ещё одно условие |
|
||||||||||||||||
|
|
|
|
|
|
′ ′ |
+ u |
′ ′ |
|
|
|
|
|||||
|
|
|
|
|
|
u1 y1 |
2 y2 = f ( x) . |
|
|
||||||||
Таким образом, мы имеем линейную систему уравнений относительно производных искомых функций
u′y + u′ y |
2 |
= 0 |
|
|||
1 |
1 |
2 |
|
|
||
′ |
′ |
′ |
′ |
|
. |
|
u1 y1 + u2 y2 = f (x) |
||||||
|
||||||
Так как определитель этой системы есть определитель Вронского для
линейно независимых функций y1(x) и |
y2 (x) , то он не равен нулю и эта |
система имеет единственное решение |
|
′ |
′ |
u1 = ϕ1 (x) , |
u2 = ϕ2 (x) . |
Проинтегрируем найденные функции |
|
u1(x) = ∫ϕ 1(x)dx , |
u2 (x) = ∫ϕ 2(x)dx |
44 |
|

и запишем частное решение неоднородного уравнения
y(x) = ∫j1(x)dx × y1(x) + ∫j2 (x)dx × y2 (x) .
Пример. |
Найти общее решение уравнения y′′ + y = 1 sin x . |
||
Решаем |
соответствующее |
однородное |
уравнение y′′ + y = 0 . Его |
характеристическое уравнение |
λ 2 + 1 = 0 |
имеет комплексные корни |
|
λ1,2 = ±i . Поэтому общее решение однородного уравнения имеет вид
yодн = C1 cos x + C2 sin x .
Применяя метод вариаций, будем искать частное решение неоднородного уравнения в виде
y(x) = u1(x)cos x + u2 (x)sin x .
Для производных искомых функций составляем систему
u′ cos x + u′ sin x = 0 |
. |
||
1 |
2 |
′ |
|
|
′ |
|
|
−u1 sin x + u2 cos x = 1 sin x |
|
||
Умножим первое из уравнений системы на cos x , второе – на ( − sin x ) и сложим. Тогда получим
′ |
(x) = −1 |
′ |
(x) = cos x sin x |
u1 |
, u2 |
и после интегрирования
u1 (x) = −x , u2 ( x) = ln sin x .
Итак, общее решение уравнения
y = C1 cos x + C2 sin x - x cos x + sin x × ln sin x .
Лекция 47. Биения и резонанс
45
Рассмотрим теперь случай, когда на колебательную систему воздействует периодическая внешняя сила. Этот случай встречается наиболее часто: давление газа на поршень в двигателе внутреннего сгорания, удары рельса на стыке по колесу железнодорожного вагона, действие струи газа или пара на лопатку турбины, удары волн о корпус судна и т.д. Для простоты анализа будем предполагать, что сопротивление среды отсутствует. В этом случае уравнение линейного осциллятора y′′ + a1 y′ + a2 y = f (t) , примет вид
y′′ + ω 2 y = Asin ω1t, |
(47.1) |
где ω1 – частота колебаний вынуждающей силы.
Решение однородного уравнения приведено (см.45.4). Это
гармонические колебания с частотой |
|
ω . |
При нахождении частного |
решения неоднородного уравнения |
|
(x) |
будем различать два случая. |
y |
Сначала пусть частота вынуждающей силы не совпадает с частотой
собственных |
колебаний, |
|
т.е. |
w1 ¹ w . |
Тогда, |
применяя метод |
|||||
неопределенных коэффициентов, |
решение |
|
(x) будем искать в виде |
||||||||
y |
|||||||||||
|
|
|
(t) = M cos w1 t + N sin w1 t . |
|
|
||||||
|
|
y |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
′′ |
Дважды дифференцируя |
y(x) и подставляя |
|
y(x) и |
|
|||||||
|
y (x) в уравнение |
||||||||||
(47.1), найдём |
M = 0, N = A/(ω 2− ω12). Таким образом, |
||||||||||
|
(t) = |
A |
sin ω1 t , |
y |
|
||
ω 2− ω 2 |
|||
|
|
1 |
|
и общее решение уравнения (47.1) представляет собой сумму двух гармонических колебаний с разными частотами
y(t) = A1 sin(ω t + γ0 ) + |
A |
sin ω1t . |
ω2 − ω12 |
Посмотрим, что произойдет, когда частота вынуждающей силы и собственная частота близки, т.е. ω ≈ ω1 . Вернемся к записи общего решения уравнения (47.1) в виде
y(t) = C1 cos ω t + C2 sin ω t + |
A |
sin ω1t . |
ω2 − ω2 |
||
|
1 |
|
46

Для простоты возьмем |
частное |
решение, |
удовлетворяющее |
нулевым |
|||
начальным условиям: |
|
′ |
|
|
|
что ему |
|
y(0) = 0, y (0) = 0 . Нетрудно проверить, |
|||||||
отвечают значения постоянных C1 = 0, C2 = - |
Aω1 |
|
|
||||
|
. |
Таким образом, |
|||||
(w2 - w21 )w |
|||||||
частное решение имеет вид |
|
|
|
|
|
|
|
|
y(t) = |
A |
(wsin w1t - w1 sin wt) . |
|
|||
|
|
|
|||||
|
(w2 - w12)w |
|
|
||||
В случае близости частот выражение в скобках можно преобразовать к следующему виду:
ωsin ω1t − ω1sin ω t ≈ ω (sinω1t − sinω t) =
=w 2cos ω1+ ω t ×sin ω1− ω t » 2w sin ω1− ω t × cos w t .
|
|
2 |
2 |
2 |
Первый множитель |
ω |
1− ω |
медленно меняющаяся функция времени, а |
|
sin |
t |
|||
|
|
2 |
|
|
второй – cos ωt быстро изменяющаяся функция. В приближённом решении уравнения
y(t) » |
2 A |
sin |
ω 1− ω |
t × cos wt |
w 2- w12 |
2 |
множитель перед быстро изменяющимся косинусом можно рассматривать как «амплитуду» этого сложного колебания, называемого биением.
Пример «сложения» таких колебаний приведён на рисунке 47.1. Теперь пусть частота внешней вынуждающей силы и собственная
частота совпадают, т.е. ω = ω1 . Найдем решение уравнения
y′′ + ω2 y = Asin ωt .
Характеристика правой части уравнения совпадает с корнем характеристического уравнения, поэтому частное решение неоднородного уравнения ищем в виде
y(t) = t(M cosωt + N sinωt) .
47
|
Y |
|
|
|
16 |
|
y(x)=8sin9x-9sin8x |
|
|
|
|
|
|
|
12 |
|
|
|
|
8 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
X |
0 |
5 |
10 |
15 |
20 |
|
||||
-4 |
|
|
|
|
-8 |
|
|
|
|
-12 |
|
|
|
|
-16 |
|
|
|
|
|
|
Рис. 47.1 |
|
|
В результате (проверьте это!) находим |
|
|
||
|
|
|
y(t) = - A |
t × cos wt . |
|
|
|
|||
|
|
|
|
|
2w |
|
|
|
|
|
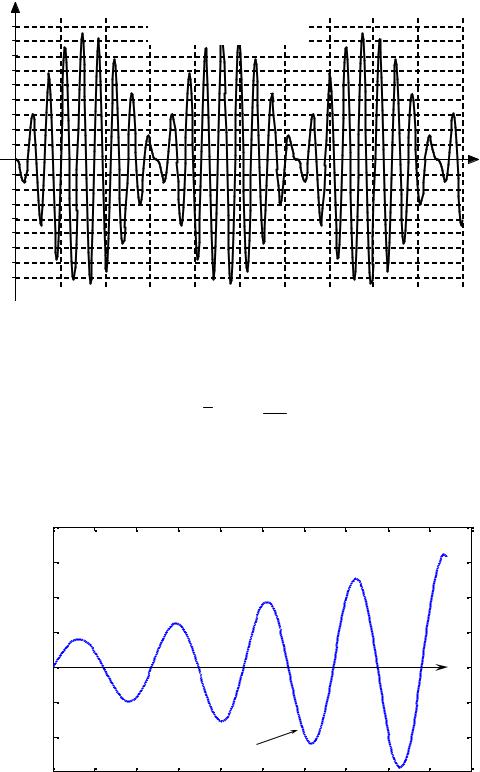
Эта функция описывает колебания частоты ω с неограниченно |
||||||||||
возрастающей «амплитудой» (см. рис. 47.2), а рассматриваемое явление |
||||||||||
называется резонансом. |
|
|
|
|
|
|
|
|
||
2 |
|
|
|
|
|
|
|
|
|
|
1.5 |
|
y''+ 9y=sin3t, |
|
|
|
|
|
|
|
|
|
|
y(0)=0,y'(0)=1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
0.5 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
-0.5 |
|
|
|
|
|
|
|
|
|
|
-1 |
y(t)=7/18sin3t-1/6tcos3t |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||||
-1.5 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
0 |
||||||||||
Рис. 47.2
Итак, мы выяснили, что при отсутствии сопротивления среды и при совпадении частоты приложенной силы с частотой собственных колебаний возникает колебательное движение той же частоты, но с неограниченно возрастающей амплитудой. В более реалистичном случае
48

учета сопротивления среды при совпадении частот |
явление резонанса |
||||||||
происходит в более «мягком» виде. |
|
|
|
|
|
||||
Рассмотрим пример |
|
|
|
|
|
|
|
||
y |
′′ |
+ 0, 2 y |
′ |
+ 1,01y = 0,5sin t, y(0) |
= 0, |
′ |
|
||
|
|
y (0) = 1. |
|
||||||
Корни характеристического уравнения комплексные |
r = −0,1 ± i , поэтому |
||||||||
решение соответствующего однородного уравнения |
|
|
|||||||
|
|
|
|
y′′ + 0, 2 y′ + 1,01y = 0 |
|
|
|
||
с заданными начальными условиями определяется функцией (см. рис. 47.3) |
|||||||||
|
|
|
|
y(t) = e−0,1t |
sint |
|
|
|
|
1 Y |
|
|
|
|
|
|
|
|
|
0.8 |
|
|
|
|
|
|
|
|
|
0.6 |
|
|
|
|
|
|
|
|
|
0.4 |
|
|
|
|
|
|
|
|
|
0.2 |
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
0 |
|
5 |
|
10 |
15 |
20 |
25 |
30 |
35 |
|
|
|
|||||||
-0.2 |
|
|
|
|
|
|
|
|
|
-0.4 |
|
|
|
|
|
y(t)=exp(-0.1t)sint |
|
||
|
|
|
|
|
|
|
|
|
|
-0.6 |
|
|
|
|
|
|
|
|
|
-0.8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 47.3 |
|
|
|
|
Решение соответствующего неоднородного уравнения с нулевыми |
|||||||||
начальными условиями имеет вид |
|
|
|
|
|
||||
y(t) = e−0,1t ( 451sin t + 1000 cost) + 50 sin t − 1000 cost 401 401 401 401
или
y(t) ≈ e−0,1t (9 /8sin t + 5/ 2cost) +1/8sin t − 5/ 2cost .
49
3 |
Y |
|
|
|
|
|
2 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
t |
0 |
10 |
20 |
30 |
40 |
50 |
60 |
|
||||||
-1 |
|
|
|
|
|
|
-2 |
|
|
|
|
|
|
-3 |
|
|
|
|
|
|
|
|
|
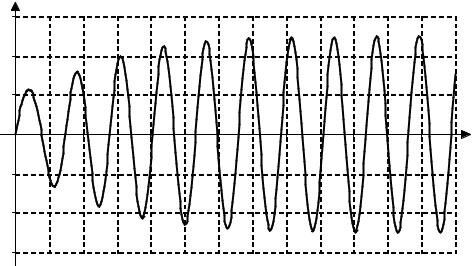
Рис. 47.4 |
|
|
|
Как видим, хотя амплитуда внешнего воздействия на колебательную систему всего 0,5, тем не менее эта внешняя сила «раскачала» систему до колебаний с амплитудой примерно 2,5. В дальнейшем система будет колебаться с частотой вынуждающей силы, а амплитуда колебаний расти не будет (см. рис. 47.4).
50
