9177

на 1-м и 2-м участках, поскольку тангенс угла ее наклона равен нагрузке q2, которая имеет другой знак и больше по величине, чем q1.

=

= ;

;

.

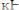
На стыке 2-го и 3-го участков к балке не приложены сосредоточенные силы и мо-

менты. Поэтому в данном сечении эпюра Мх не имеет разрыва и излома, то есть гладкая.

Квадратная парабола выпуклостью вверх и имеет экстремум в том сечении, где эпюра Qy

пересекает ось (Qy= 0). Для построения параболы в данном случае следует третье значение

считать не в середине участка (как на участке 2), а в месте экстремума.

Экстремальные значения усилий принято вычислять, поскольку часто они явля-

некотором участке, следует сначала найти его расположение, то есть положение сече-

Экстремальное значение равно:

Проводим квадратную параболу через три точки.

Эпюры Qy и Мх построены.

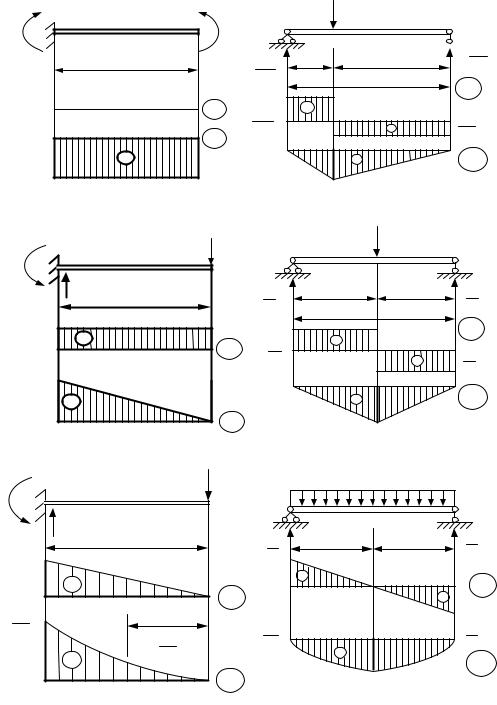
Эпюры усилий в простейших балках

Очень часто в конструкциях встречаются балки, имеющие простую расчетную схему и нагрузку. Характер усилий для ряда таких балок грамотный инженер должен помнить наизусть. Эти балки вместе с эпюрами Qy и Mx приведены на рис. 3.15 – 3.20.

Fa

Рис. 3.19 Рис. 3.20

4. ЦЕНТРАЛЬНОЕ РАСТЯЖЕНИЕ–СЖАТИЕ (ЦРС)

4.1. Напряжение в поперечных сечениях стержня

Нормальная сила N приложена в центре тяжести сечения, является равнодействую-

щей внутренних сил в сечении и, в соответствии с этим, определяется следующим образом:

(4.1)

Считается, что при ЦРС нормальное напряжение в любом сечении стержня посто-

янно, то есть поперечные сечения перемещаются параллельно друг другу, а все поверхно-

стные и внутренние продольные волокна удлинятся одинаково, что соответствует гипо-

тезе плоских сечений. Гипотеза плоских сечений была установлена Я. Бернулли в результате экспериментов: при растяжении стержня продольные и поперечные риски, на-

несенные на его поверхности до деформации, остаются прямолинейными и взаимно пер-

пендикулярными, изменяются лишь расстояния между ними (между поперечными риска-

где A − площадь поперечного сечения стержня.

В сечениях, близких к месту приложения внешних сил, гипотеза Бернулли наруша-

ется: сечения искривляются, и напряжения в них распределяются неравномерно. По мере удаления от сечений, в которых приложены силы, напряжения выравниваются, и в сече-

ниях, удаленных от места приложения сил на расстояние, равное наибольшему из разме-

ров поперечного сечения, напряжения можно считать распределенными по сечению рав-

номерно. Это положение, называемое принципом СенВенана, позволяет при опре-

делении напряжений в сечениях, достаточно удаленных от мест приложения внешних сил,

не учитывать способ их приложения, заменять систему внешних сил статически эквива-

лентной системой.

Рис. 4.1

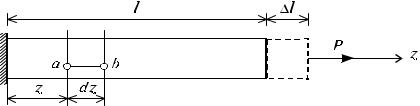
Высказанное предположение о равномерном распределении нормальных напряже-

ний в поперечном сечении справедливо для участков, достаточно удаленных от мест: рез-

кого изменения площади поперечного сечения (рис. 4.1, в); скачкообразного изменения внешних нагрузок; скачкообразного изменения физико-механических характеристик кон-

струкций.

Нормальные напряжения при сжатии определяют так же, как и при растяжении, но считают отрицательными.

В инженерных сооружениях встречаются растянутые или сжатые элементы,

имеющие отверстия. В сечениях с отверстием определяют осредненные нормальные на-

пряжения по формуле:

где Ант − площадь поперечного сечения нетто с учетом ослабления.

4.2. Деформации и перемещения. Закон Гука

Рассмотрим однородный стержень с одним концом, жестко заделанным, и другим -

свободным, к которому приложена центральная продольная сила Р (рис. 4.2). До нагру-

жения стержня его длина равнялась l - после нагружения она увеличилась на ℓ (рис.4.2).

Величину ℓ называют абсолютной продольной деформацией (абсолютным удли-

нением) стержня. В большинстве случаев оно мало по сравнению с его первоначальной длиной l (∆l<<l).

Рис.4.2

Согласно гипотезе плоских сечений все участки стержня находятся в одинаковых

условиях. Бесконечно малый элемент ab длиной dz при растяжении увеличивает свою длину на величину dz и его относительная деформация будет составлять:

В пределах малых деформаций при простом растяжении или сжатии закон Гука за-

писывается в следующем виде (нормальные напряжения в поперечном сечении прямо

пропорциональны относительной линейной продольной деформации ):

Величина Е представляет собой коэффициент пропорциональности, называемый

модулем упругости материала первого рода (модуль продольной упругости). Его вели-

чина постоянна для каждого материала. Он характеризует жесткость материала, т.е. спо-

собность сопротивляться деформированию под действием внешней нагрузки, определяет-

ся экспериментальными исследованиями материала конструкции.

В поперечных направлениях стержень деформируется, возникают поперечные де-

формации ε’ . Отношение относительной поперечной деформации ε' к относительной продольной деформации ε, взятое по модулю, есть для каждого материала величина по-

стоянная и называется коэффициентом Пуассона:

4.3. Физико-механические свойства металлов

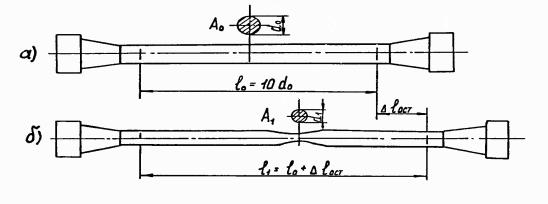
Испытания образцов на растяжение проводятся с целью экспериментального опре-

деления механических характеристик материалов . Наиболее распространенными в на-

стоящее время являются испытания цилиндрических и плоских образцов в условиях од-

ноосного растяжения.

Широкому применению этого вида испытаний способствует относительная про-

стота их осуществления, так как имеется большой парк разрывных и универсальных ис-

пытательных машин (например, УММ-20 или МИ-40КУ). Испытание на растяжение за-

ключается в плавном деформировании закрепленного в захватах испытательной машины образца из исследуемого материала до наступления его разрушения. При этом специаль-

ные приборы фиксируют зависимость абсолютного удлинения образца от прикладывае-

мой к нему продольной растягивающей нагрузки.

Рис.4.3

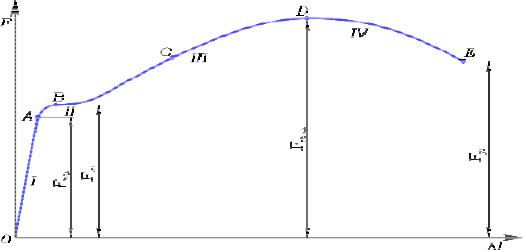
В процессе испытаний измеряются сила, действующая на образец, и удлинение его расчетного участка. Результатом испытаний является графическая диаграмма растяже-

ния.

Рис.4.3. Диаграмма растяжения образца из малоуглеродистой стали

Как видно из рисунка, диаграмма имеет четыре характерных участка: I - участок пропорциональности;

II - участок текучести;

III - участок самоупрочнения; IV - участок разрушения.

Рассмотрим подробнее процесс построения диаграммы.

В самом начале испытания на растяжение, растягивающая сила F, а следовательно, и де-

формация l стержня равны нулю, поэтому диаграмма начинается из точки пересечения соответствующих осей (точка О).

На участке I до точки A диаграмма вычерчивается в виде прямой линии. Это говорит о том, что на данном отрезке диаграммы, деформации стержня l растут пропорционально увеличивающейся нагрузке F. На этом участке выполняется закон Гука – математическая линейная зависимость между напряжениями и деформациями: ε Е = σ, где Е – модуль уп-

ругости (Юнга) равный тангенсу угла наклона прямого участка диаграммы к оси абсцисс.

После прохождения точки А диаграмма резко меняет свое направление и на участке II на-

чинающемся в точке B линия какое-то время идет практически параллельно оси l, то есть деформации стержня увеличиваются при практически одном и том же значении на-

грузки. Этот участок диаграммы называется площадкой текучести. В этот момент в ме-

талле образца начинают происходить необратимые изменения. Перестраивается кристал-

лическая решетка металла. При этом наблюдается эффект его самоупрочнения.

При дальнейшем повышении нагрузки диаграмма снова "идет вверх" (участок III) и в точ-

ке D растягивающее усилие достигает максимального значения. В этот момент в рабочей

части испытуемого образца появляется локальное утоньшение, так называемая "шейка",

вызванное нарушениями структуры материала (образованием пустот, микротрещин и т.д.).

Рис.4.4. Стальной образец с "шейкой"

Вследствие утоньшения, и следовательно, уменьшения площади поперечного сечения об-

разца, растягивающее усилие необходимое для его растяжения уменьшается, и кривая диаграммы "идет вниз".

В точке E происходит разрыв образца. Разрывается образец в сечении, где была образова-

на "шейка"

По диаграмме также можно определить величину упругих и остаточных деформаций в

любой момент процесса испытания.

Для получения непосредственно механических характеристик металла образца диаграмму растяжения необходимо преобразовать в диаграмму напряжений.

Для полученных значений точек диаграммы определяются соответствующие им нормальные напряжения σ, по формуле:

σi=Fi / A0

где: Fi - значение растягивающей силы в характерной точке диаграммы;

A0 - площадь поперечного сечения рабочей части образца,

и относительные деформации ε:

εi= l / l0

где l0 - начальная длина рабочей части испытуемого образца

По полученным данным в системе координат σ-ε строится диаграмма напряжений (рис.4.5)

Рис. 4.5. Условная и истинная диаграмма напряжений для малоуглеродистой стали

По этой диаграмме определяются следующие механические характеристики материала:

∙Предел пропорциональности σпц - максимальное напряжение, при котором вы-

полняется закон Гука. Определяется как крайняя верхняя точка начального прямо-

линейного участка диаграммы.

∙Предел текучести материала σт – наименьшее напряжение, при котором деформа-

ция увеличивается без заметного увеличения нагрузки. На диаграмме – точка, по-

сле которой линия диаграммы некоторое время движется параллельно оси дефор-

маций ε. Практически горизонтальный участок диаграммы, следующий за преде-

лом текучести, называется площадкой текучести.

∙Предел прочности (временное сопротивление) σВ (σпч) - напряжение, соответст-

вующее максимальной нагрузке, предшествующей разрушению образца. При от-

сутствии площадки текучести (что характерно для диаграмм растяжения большин-

ства материалов, после предварительной пластической деформации) определяют условный предел текучести 0,2σв, который называется техническим пределом

прочности. Условным пределом текучести напряжение, при котором остаточная

(пластическая) деформация составляет 0,2 %.

Конечная точка диаграммы, при которой происходит разрыв образца: - условное напряжение разрыва

σру = Fр / A0 ; - истинное напряжение при разрыве

σри = Fр / Aш ;

здесь Aш - площадь поперечного сечения в области "шейки" образца.

При более тонких испытаниях по данной диаграмме можно определить предел уп-

ругости стали. Пределом упругости σупр называют максимальное напряжение, при ко-

тором не возникают остаточные деформации. Принято считать за максимальное то на-

пряжение, при котором в испытуемом образце появляются деформации 0,05%.

На рисунке штриховой линией показан фрагмент истинной диаграммы напряже-

ний. Возрастание напряжений после прохождения предела прочности объясняется тем,

что в этот момент в рабочей части образца образуется локальное утоньшение ("шейка")

уменьшающая его площадь поперечного сечения A, что в свою очередь приводит к увели-

чению напряжений при уменьшении растягивающей силы.

Кроме того, по диаграмме напряжений можно приближенно определить величину

он определяется как отношение напряжений и относительных деформаций, для любой точки диаграммы, расположенной от ее начала до предела пропорциональности, либо как тангенс угла наклона начального участка диаграммы к оси ε.

Еще одна важная характеристика материала – это оценка интенсивности дефор-

мации εи, где применяют такие понятия как: относительная продольная деформации εпр,

приходящиеся на единицу длины или ε′ относительная поперечная, приходящаяся на

единицу параметра сечения (высота, ширина). Продольная и поперечная деформации свя-

заны соотношением (закон Пуассона) ν = ε′/εпр, где μ – коэффициент Пуассона – по-

стоянная материала в пределах упругости.

Предел пропорциональности, предел упругости, предел текучести, модуль упругости и коэффициент поперечной деформации (коэффициент Пуассон) харак-

теризуют упругие свойства материала необходимые для создания прочных и надеж-

ных конструкций.

4.4. Расчеты на прочность при ЦРС по методу допускаемых нагрузок

Метод расчета строительных конструкций и их элементов по допускаемым напря-

жениям основан на предположении, что критерием надежности конструкции будет вы-

полнение следующего условия прочности:

где σmax – наибольшее напряжение, возникающее в одной из точек опасного сече-

ния и определяемое расчетом; [σ] – допускаемое (предельное) для данного материала на-

пряжение, полученное на основании экспериментальных исследований.

Допускаемое напряжение определяется по формуле:

[σ] = σ0 , n

где σ0 – опасное напряжение; n – коэффициент запаса прочности.

Для пластичных материалов за опасное напряжение σ0 принимается предел теку-

чести σт ; для хрупких материалов – временное сопротивление (предел прочности) σв.

Значение коэффициента запаса прочности, а следовательно, и допускаемого на-

пряжения зависит от многих факторов. Основными факторами, которые влияют на выбор его значения, являются:

1) соответствие механических свойств материала конструкции и отдельно испытан-

ных образцов;

2)учет конкретных условий работы рассчитываемой конструкции;

3)метод определения напряжений (степень точности этого метода);

4)неточность задания внешней нагрузки;

5)долговечность и значимость проектируемого сооружения или машины.

Значения допускаемых напряжений или коэффициентов запаса прочности устанав-

ливаются техническими условиями и нормами проектирования. Для строительных сталей значение коэффициента запаса прочности принимается n = 1,4÷1,6; для хрупких материа-

лов n = 2,5÷3,5; для древесины n = 3,5÷6.

При центральном растяжении-сжатии нормальные напряжения в поперечных сече-

ниях, достаточно удаленных от места приложения сил, постоянны (принцип Сен-Венана)

и определяются по формуле:

где σ – нормальное напряжение; А – " чистая" площадь поперечного сечения бруса после вычета возможных ослаблений сечения отверстиями, т.е. А = Аnetto.

Если площадь поперечного сечения бруса постоянна по длине, то условие прочно-

сти для пластичного материала имеет вид:

где |max N| – наибольшее значение продольной силы по абсолютной величине бе-

рется из эпюры N (сечение, где имеется |max N|, является опасным); [σ] – расчетное со-

противление материала по пределу текучести.

Если брус выполнен из хрупкого материала, т.е. когда расчетные сопротивления на растяжение и сжатие различны [σ]с ≠ [σ]р , то условие прочности имеет следующий вид:

max σр = max Nр / А ≤ [σ]р

(4.15)

|max σс| = |max Nс| / А ≤ [σ]с

где maxNр – наибольшая растягивающая продольная сила (на эпюре N имеет знак

"плюс"); |max Nс| – наибольшая по абсолютной величине сжимающая продольная сила