9070

Кулагин Юрий Михайлович

Лихачева Светлана Юрьевна

Страхов Вячеслав Петрович

Сухов Михаил Фёдорович

Геометрические характеристики плоских сечений

Методические указания к расчётно-проектировочной работе №1

по курсу «Сопротивление материалов» для студентов направления – «Строительство»

- 3 -

При расчётах стержней на прочность и жёсткость используется не только площадь поперечного сечения стержней, но и более сложные геометрические характеристики сечений, которые необходимо ввести и научиться пользоваться ими.

1. Статические моменты плоских фигур. Центр тяжести

Рассмотрим интегральное определение статических моментов плоских фигур.

Разбиваем заданную фигуру на элементарные площадки dA (рис. 1).

Умножаем площадь каждой площадки на координаты их центра тяжести х и у. Интегрируя по площади сечения, в итоге получим следующие результаты:

Sx и Sy являются статическими моментами плоской фигуры относительно осей х и у.

Статические моменты выражаются в см3, мм3 и т. д. и могут принимать любые значения, т. е. могут быть положительными, отрицательными и равными нулю.

Если положение центра тяжести фигуры (точка С) и её площадь А известны, то статические моменты определяются по формулам

Sx = уС · А, Sу = хС · А.

Из формул следует, что статические моменты равны нулю относительно

центральных осей. Оси симметрии являются центральными осями.

Если сечение можно разбить на ряд простых фигур (прямоугольники,

треугольники, круг, полукруг и т. д.), площади и центры тяжести которых

- 4 -

известны, координаты центра тяжести сечения определяются по формулам,

полученным ранее:

Рассмотрим общую схему вычисления координат центра тяжести на примере плоской, однородной фигуры:

1)Относим фигуру (сечение) к произвольно выбранной системе координат х, у.

2)Разбиваем заданную фигуру на простейшие фигуры, площади Аi и

координаты центра тяжести хi, уi которых известны (прямоугольник,

квадрат, круг, треугольник и т.д.). Если заданная фигура имеет вырезы, то площадь выреза можно принимать со знаком минус.

3)Подставляя площади и координаты центра тяжести в формулы для

хС и уС, найдём положение относительно осей х и у центра тяжести

(точка С) заданной фигуры (сечения).

2. Моменты инерции сечений

Для фигуры (сечения), показанной на рис. 1, вводим следующие новые

Введённые моменты инерции имеют размерность мм4, см4 и т. д.

Осевые моменты инерции и полярный момент инерции всегда положительны и не равны нулю.

Складывая осевые моменты инерции и учитывая, что 2 х2 у2 (см.

рис. 1), получим следующее равенство

Jx Jy J ,

- 5 -

т.е. сумма осевых моментов инерции относительно двух взаимно перпендикулярных осей равна полярному моменту инерции относительно точки пересечения этих осей.

Центробежный момент инерции может быть положительным,

отрицательным и равным нулю.

Оси, относительно которых центробежный момент инерции равен нулю:Jxy 0, называют главными осями инерции.

Если оси х и у являются осями симметрии, то центробежный момент инерции фигуры относительно этих осей будет равен нулю.

Следовательно, оси симметрии – главные, центральные оси сечения.

Осевой момент инерции сложной фигуры относительно некоторой оси равен сумме осевых моментов инерции составляющих её частей относительно этой же оси. Аналогичное свойство справедливо для полярного и центробежного моментов инерции.

3. Моменты инерции простейших фигур

1). Моменты инерции прямоугольного сечения шириной b и высотой h.

- 6 -

Выделим линиями, параллельными оси х, элементарную полоску высотой dy и шириной b (рис. 2). Площадь этой полоски dA = b dy, а координата её центра тяжести – у. Пределы интегрирования: от y = - h/2 до y = + h/2.

Вычислим осевой момент инерции прямоугольника относительно оси симметрии х:

Оси х и у – оси симметрии фигуры, поэтому Jxy = 0.

Для прямоугольного сечения (рис. 42) моменты инерции равны разности моментов инерции большого прямоугольника и малого прямоугольника:

- 7 -

В строительстве широкое применение находит прокатная сталь. Сечения прокатных профилей показаны на рис. 4:

- 8 -

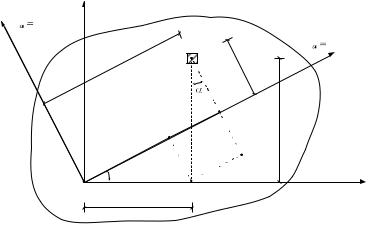
Но Sxc 0, т.к. статические моменты фигур относительно центральных

осей равны нулю. Окончательно получаем

Jx JxC a2 A.

Для оси у аналогично получим

Jy JyC b2 A.

Проведя вычисления для центробежного момента инерции, получим

Из формул для осевых моментов инерции следует, что для всех параллельных осей наименьшее значение осевые моменты инерции имеют относительно центральных осей хс и ус.

Если заданную фигуру можно разбить на простейшие фигуры, то полученные формулы вычисления моментов инерции при параллельном переносе осей можно записать в следующем виде

заданной системы координат х, у известны. Повернём заданную систему

- 9 -

координат вокруг начала координат на произвольный угол ά (рис. 6).

Положительным будем считать угол поворота от положительного значения х к положительному значению у. На рис. 6 показан положительный угол поворота для заданной системы координат.

Формулы, связывающие координаты центра тяжести элементарной площадки dA в новой (повёрнутой) и старой системах координат, приведены на рис. 6.

Момент инерции сечения относительно оси u будет равен:

Ju Jx cos2 y2 dA 2sin cos xydA sin2 x2 dA.

A A A

Первый и третий интегралы представляют собой моменты инерции Jx и

Jy относительно старых осей, второй интеграл – центробежный момент инерции Jxy. Выполняя аналогичные вычисления для другой оси и для центробежного момента сопротивления, получим следующие формулы:

Складывая формулы для осевых моментов инерции, получим следующее равенство:

Ju + Jv = Jx + Jy = Jp const ,

т.е. при повороте осей значения осевых моментов инерции относительно этих осей изменяются, но их сумма остаётся постоянной, поскольку равна полярному моменту инерции.

6. Главные оси инерции. Главные моменты инерции

Если оси координат поворачивать в своей плоскости вокруг начала координат, то полярный момент инерции останется неизменным, а осевые моменты инерции будут изменяться, причём Jx + Jy = const.

- 10 -