Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Нижегородский Государственный Архитектурно-Строительный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

9014

.pdf

Скачиваний:

Добавлен:

25.11.2023

Размер:

2.13 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 98 9 > Следующая >>>

Задания для самостоятельной работы:

В задачах 1 - 31 построить кривые. Там, где необходимо, преобразовать уравнения кривых параллельным переносом осей координат. Построить новые и старые оси координат.

		2		2								2 2
1.	4x		3y 24						17.	x y 6y70
1.					.				17.									.
		2		2									2
2.	4x 3y 600								18.		x 4x8y120
2.						.			18.									.
		2 2									2x 3xy4y 0
3.	2x y 4x80								19.		2x 3xy4y 0
3.							.		19.									.
		2											2 2
4.	8x 9y 110								20.			x y 2x10y260
4.					.				20.											.
	x 2xy3y 4												2
5.	x 2xy3y 4								21.				x 2x 3y 0
5.					.				21.								.
		2		2									2		2
6.	x 3y 2x 0								22.			x 2y 4y20
6.						.			22.										.
		2											2		2
7.	x 2x5y10								23.		3x 10y 2 0
7.							.		23.									.
	3x xy3y 20												2
8.	3x xy3y 20								24.				x x y 2 0
8.						.			24.									.
		2		2									2 2
9.	x 3y 2x 0								25.				y x 6y50
9.						.			25.									.
		2											2		2
10.		y 2x2y70							26.			3x		5y		0
10.							.		26.								.
		xy0,5y 2x 3											2
		xy0,5y 2x 3											y 2x 4y 0
11.						.			27.				y 2x 4y 0
11.						.			27.								.
		x 23xy3y 0											2
		x 23xy3y 0											x 9y 4 0
12.							.		28.				x 9y 4 0
12.							.		28.								.
		2		2										2 2
13. x 4y 0.									29.				16x 9y 90y810
13. x 4y 0.									29.											.
			2										2 2
14.		x 8x2y160							30.				x y 2x6y80
14.							.		30.											.
		2 2													2 2
15.		x y 2x4y60							31.				36x4y72x40y41
15.								.	31.												.
		2
16.		y 8x2y160
16.							.

Элементы аналитической геометрии в пространстве

Поверхность в пространстве, как правило, можно рассматривать как геометрическое место точек, удовлетворяющих какому либо условию.

Прямоугольная система координат в Oxyz пространстве позволяет установить взаимно однозначное соответствие между точками пространства и

тройками чисел x, y и z – их координатами. Свойство, общее всем точкам поверхности, можно записать в виде уравнения, связывающего координаты всех точек поверхности.

Уравнением данной поверхности в прямоугольной системе координат

Oxyz называется такое уравнение F(x, y, z) 0 с тремя переменными x, y и z

, которому удовлетворяют координаты каждой точки, лежащей на поверхности,

и не удовлетворяют координаты точек, не лежащих на этой поверхности.

Простейшей поверхностью является плоскость. Плоскость в пространстве

Oxyz можно задать разными способами. Каждому из них соответствует определенный вид ее уравнения.

§1. Плоскость в пространстве

1.Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору

Пусть в пространстве Oxyz плоскость задана точкой				M 0 (x0 , y0 , z0 ) и вектором

n A, B,C , перпендикулярным этой плоскости.

	n A, B, C
M 0			Рис.1
M 0		M
		M


Возьмем на плоскости произвольную			точку M (x, y, z) и рассмотрим вектор

M 0 M x x0 ; y y0 ; z z0 . Так как векторы n и M 0 M				перпендикулярны, то их

скалярное произведение равно нулю: n			M 0 M 0 , то есть
	A x x0 B y y0 C (z z0 ) 0 .			(1)

Уравнение (1) называется уравнением плоскости, проходящей через заданную точку перпендикулярно заданному вектору.

Отметим, что вектор перпендикулярный данной плоскости называется

нормальным вектором этой плоскости или вектором нормали.

2. Общее уравнение плоскости
Если в уравнении (1) раскрыть скобки и обозначить	C Ax0 By0 Cz0 , то
получим общее уравнение плоскости:
Ax By Cz D 0.	(2)

Пример 1. Составить уравнение плоскости, проходящей через точку M 0 1; 2;3 и

перпендикулярной вектору PQ , если P 0;1;4 и Q 1; 2;6 .

Решение. Находим координаты вектора PQ , являющегося вектором нормали


плоскости n PQ 1;1; 2 .
Подставляя в уравнение (1) координаты точки M 0 1; 2;3 и координаты вектора

n 1;1;2 , находим искомое уравнение плоскости
1 x 1 1 y 2 2(z 3) 0 или		x 1 y 2 2z 6 0
или x y 2z 7 0 .
3. Уравнение плоскости в отрезках
Из (2) следует	Ax By Сz D и далее, предполагая, что		D 0 (т.е. плоскость

не проходит через начало координат) и, разделив обе части этого уравнения на

D , получим уравнение

(3)

в котором

величины отрезков, которые плоскость

«отрезает»

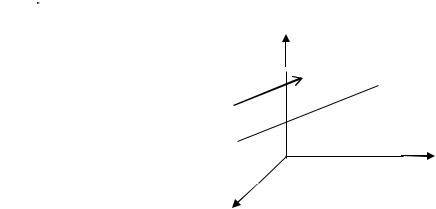
от осей координат (см. рис. 2).

3. Уравнение плоскости, проходящей через три заданные точки

Три точки пространства, не лежащие на одной прямой, определяют единственную плоскость. Уравнение плоскости, проходящей через три

заданные
точки M1 (x1 , y1 , z1 ),	M 2 (x2 , y2 , z2 ), M 3 (x3 , y3 , z3 ),				имеет вид:
		x x1	y y1	z z1
		x x1	y y1	z z1
		x2 x1	y2 y1	z2 z1		0
		x3 x1	y3 y1	z3	z1	(4)
						(4)
Раскладывая	этот определитель по элементам первой строки, приведем
его к линейному уравнению относительно					x, y, z вида (2).

Взаимное расположение двух плоскостей.

Пусть заданы две плоскости П1 и П 2 уравнениями (см. рис. 3).

A1 x B1 y C1z D1 0 ,

A2 x B2 y C2 z D2 0 .


a)		n2			b)	n1
a)		n2			b)	n1
	П 2		n1




П	1				П1
	1
						П	2
				Рис. 3	n2
					n2

Найдем угол между ними в предположении, что они пересекаются.

Пересекаясь, плоскости образуют две пары равных двугранных углов. Углом

между плоскостями

П1

и П2

будем считать меньший из этих двугранных

углов (см. рис. 3).

Выразим угол

между

плоскостями

через

угол

между

A , B ,C и

A , B ,C

Если угол

нормальными к ним векторами

острый, то (как углы с взаимно перпендикулярными сторонами). Если

же угол – тупой, то	(см. рис. 3 b) ), поэтому														cos cos . В
итоге для вычисления угла			между плоскостями имеем формулу
									A A	B B C C

		n	n
cos		1		2					1 2	1	2		1	2
									1 2	1	2		1	2

		n1		n2			A2	B2		C 2		A2	B	2 C 2
						1		1		1	2		2		2
					(5)

В частности, условие перпендикулярности и условие параллельности

двух плоскостей имеют вид

П1 П2

A1 A2 B1 B2 C1C2 0;

П1 || П2

В последнем случае, если дополнительно выполняется равенство

то эти плоскости совпадают.

Расстояние от точки до плоскости

Пусть заданы плоскость уравнением Ax By Cz D 0 и точка

M 0 (x0, y0 , z0 ) . Требуется найти расстояние от точки M 0 до плоскости.

Расстояние d от точки M 0 до плоскости равно модулю проекции вектора M1M 0 ,

где M 0 - произвольная точка плоскости, на направление нормального вектора

. Следовательно, n A; B;C

d | прn M1M 0 |

______

| A(x0 x1 ) B( y0 y1 ) C(z0 z1 ) |

n M1M 0

_______

| n |

A2 B2

| Ax0 By0 Cz0 Ax1 By1 Cz1 |

Так как точка M1 принадлежит плоскости, то Ax1 By1 Cz1 D 0,

т.е.

D Ax1 By1 Cz1. Поэтому

| Ax0

By0

Cz0 D |

(6)

A2 B2 C2

что и требовалось получить.

Пример 12. Найти расстояние от точки M 0 (2, 1, 4) до плоскости

3x 4y 2z 1 0.
Решение. По формуле (7) получаем
	\| 3 2 4 ( 1) 2		4 1 \|
d	\| 3 2 4 ( 1) 2		4 1 \|	5	5 29	.


		9 16 4	29		29

Задания для самостоятельной работы:

1.Найти точки пересечения плоскости 2x3y4z 240с осями координат. Плоскость построить.

2.Построить плоскости:

1)2x 3y 5z 70; 2) 4x 3y z 0; 3) 2x 3z 6;

4)	2y 3z 12 2y 3x 4			6)	2x 5z 0		3x 2y 0
4)		; 5)	;	6)		; 7)		;
8)	y z 0;	9) 2z 7 0;	10)	3y 5 0; 11) 3x 6 0;				12) 2z 0;
13) 3y 0 ;		14) x 0
3.	Дано уравнение плоскости				x 2y 3z 60
3.	Дано уравнение плоскости						. Написать для нее
	уравнение в отрезках. Плоскость построить.
4.	Составить	уравнение	плоскости,			которая	проходит	через точку

M2; 3; 4 и отсекает на координатных осях отрезки одинаковой

величины. Плоскость построить.

b 1; 2;1.

M2; 1;3 и

M3;4; 5

5.	Составить уравнение			плоскости,	которая	проходит через точки
	M 1;4; 1		M 13;2; 10
	1	,	2	и отсекает на осях абсцисс и аппликат
	отрезки одинаковой длины. Плоскость построить.
6.	Плоскость проходит через точку M6; 10;1 и отсекает на оси абсцисс
	отрезок	a 3 ,	а на оси аппликат		отрезок	c 2 . Составить для этой

плоскости уравнение в отрезках. Плоскость построить.

7.Написать уравнение плоскости, проходящей через точку M1; 2;3 и

перпендикулярной вектору OM .

8.Составить уравнение плоскости, проходящей через точку M3;4; 5 параллельно плоскости 2x3y2z10.

9.Установить, какие из следующих пар уравнений определяют параллельные плоскости:

1)2x 3y 5z 70 и 2x 3y 5z 30;

2)4x 2y 4z 50 и 2x y 2z 1 0;

3) x 3z 2 0 и 2x 6z 7 0

10.Составить уравнение плоскости, которая проходит через начало координат параллельно плоскости 5x 3y 2z 30.

11.Составить уравнение плоскости, которая проходит через точку M3; 2; 7 параллельно плоскости 2x 3z 5 0.

12.Даны две точки M3; 1;2 и N4; 2; 1. Составить уравнение

плоскости, проходящей через точку M перпендикулярно вектору MN .

13. Составить уравнение плоскости, проходящей через точку параллельно двум векторам a 3;1; 1 и

14. Составить уравнение плоскости, проходящей через точки N 3;1;2 параллельно вектору a 3; 1;4 .

15.Написать уравнение плоскости, проходящей через точку 0;0; 2 и

перпендикулярной к плоскостям x y z 0 и 2 y x .

16.Составить уравнение плоскости, проходящей через три точки

			77
M 3; 1;2		M 4; 1; 1		M 2;0;2
1	,		и
		2		3 .

17. Установить, какие из следующих пар уравнений определяют перпендикулярные плоскости:

1)3x y 2z 50, x 9y 3z 2 0;

2)2x 3y z 30, x y z 5 0;

	2x 5y z 0		x 2z 3 0
3)		,
			;
4)	x y z 1		2x 3y z 7 0
		,	.
18. Составить		уравнение плоскости, которая проходит через начало

координат перпендикулярно к двум плоскостям: 2x y 3z 1 0и x 2y z 0.

19.Составить уравнение плоскости, которая проходит через точку

M2; 1;1 перпендикулярно плоскости 2x z 1 0 и параллельно

вектору b 1; 2;1 .

20.Установить, что три плоскости x 2y z 7 0, 2x y z 2 0и x 3y 2z 110имеют одну общую точку. Вычислить ее координаты.

21.Составить уравнение плоскости, которая проходит через:

точки

M 0;1;3

M 2;4;5

параллельно оси

;

точки

M 3;1;0

M 1;3;0

параллельно оси

;

точки

M 3;0;3

M 5;0;0

параллельно оси

22.

Написать уравнение плоскости, которая проходит через точку

M2; 4;3 и через :

ось OX ;

2) ось OY ;

3) ось

OZ .

23.

Составить уравнение плоскости, которая проходит:

1) через точку

M2; 3;3 параллельно плоскости

XOY ;

2) через точку

N1; 2;4 параллельно плоскости

XOZ ;

3) через точку

P 5;2; 1 параллельно плоскости

YOZ .

24.

Вычислить расстояние d точки M от плоскости в каждом из следующих

случаев:

1)	M 2; 4;3	2x y 2z 3 0		M2; 1; 1 16x12y 15z 0
1)	,		; 2)	,			;
3)	M1;2; 3 ,	5y 4 0;	4)	M3; 6;7 ,		4x 3z 1 0.
25. Вычислить расстояние d			от точки P 1;1; 2			до плоскости,
	проходящей	через три	точки:	M1; 1;1		M 2;1;3
	проходящей	через три	точки:	1	,	2	,
	M4; 5; 2
	3	.

26.В каждом из следующих случаев вычислить расстояние между двумя параллельными плоскостями:

1)x 2y 2z 120 и x 2y 2z 6 0;

2)2x3y 6z 140и 4x6y12z 210.

27.На оси OY найти точку, отстоящую от плоскости x 2y 2z 2 0на

расстоянии d 4 .

28.На оси OZ найти точку, равноудаленную от точки M1; 2;0 и от плоскости 3x 2y 6z 90.

29.На оси OX найти точку, равноудаленную от двух плоскостей:

12x16y15z10, 2x 2y z 1 0.

§2. Прямая в пространстве

1.Каноническое уравнение прямой

Положение прямой l в пространстве однозначно определено, если задана некоторая точка M 0 x0 ; y0 ; z0 на этой прямой и так называемый

направляющий вектор , параллельный данной прямой. p m, n, p

Возьмем на прямой произвольную точку M (x, y, z) и рассмотрим вектор

M 0 M x x0 ; y y0 ; z z0 .

M 0

Рис. 1

Так как векторы p и M 0 M коллинеарны, то их координаты пропорциональны

x x0	y y0	z z0	.	(1)
m	n
		p

Полученное уравнение называется каноническим уравнением плоскости.

2. Параметрическое уравнение прямой

В уравнении (1) введем обозначение

x x0

y y0

z z0

где t

называется

параметром ( t ), тогда

x x0

x x

y y0

y y

z z0

z z

Отсюда получаем:

x x0

m t

n t

(2)

p t

Это так называемые параметрические уравнения прямой.

3. Уравнение прямой, проходящей через две заданные точки

Пусть прямая l проходит через две точки M1 (x1 , y1 , z1 ) и M 2 (x2 , y2 , z2 ) . Нетрудно понять, что вектор M1M 2 x2 x1; y2 y1 , z2 z1 можно считать направляющим вектором данной прямой. Отсюда, используя уравнение (1),

получим уравнение прямой, проходящей через две заданные точки.

<<< < Предыдущая 1 2 3 4 5 6 78 / 98 9 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
21.11.2023160.72 Кб0901.pdf
#
25.11.20232.13 Mб09010.pdf
#
25.11.20232.13 Mб09011.pdf
#
25.11.20232.13 Mб09012.pdf
#
25.11.20232.13 Mб09013.pdf
#
25.11.20232.13 Mб09014.pdf
#
25.11.20232.13 Mб09015.pdf
#
25.11.20232.14 Mб09016.pdf
#
25.11.20232.14 Mб09017.pdf
#
25.11.20232.14 Mб19018.pdf
#
25.11.20232.14 Mб19019.pdf