8802

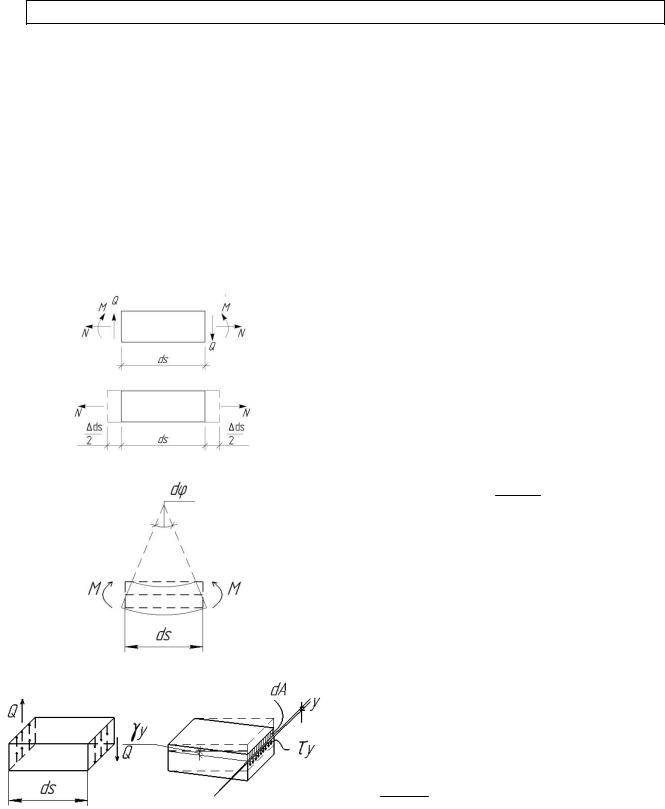
перемещениях, вызванных силами первого состояния (теорема Бетти).

9.2.Работа внутренних сил. Потенциальная энергия деформации системы

Всооружении при его нагружении внешними силами за счет деформаций будет происходить накопление внутренней энергии, которая называется потенциальная энергия деформации системы (V).

Вусловиях идеальной упругости согласно законам сохранения механической энергии, работа внешних сил будет полностью переходить в потенциальную энергию деформации, т.е. A = V. Процесс накопления потенциальной энергии происходит за счет работы сил взаимодействия между частицами материала конструкции. В процессе нагружения внешние силы будут совершать положительную работу, величина которой определяется по теореме Клапейрона, а внутренние силы - отрицательную работу (при разгрузке – наоборот).

Выразим потенциальную энергию деформации в зависимости от возникающих в сечениях внутренних сил. Для этого рассмотрим бесконечно малый элемент под действием усилий M, Q и N , по отношению к которому их можно считать внешними силами.

При действии продольной силы N элемент ds

удлинится на величину ds . По закону Гука

D = N × ds ds ,

E × A

где E – модуль упругости, A – площадь, (E.A)

– жесткость стержня при растяжении (сжатии). Действительная работа внутренних сил N за счет деформации малого элемента ds будет

При действии изгибающего момента элемент ds изогнется (см. рисунок). Нейтральная ось искривится, но длина ее не изменится. Взаимный угол поворота соседних сечений также выражается в соответствии с законом Гука:

ϕ = M × ds

d , где I – момент инерции сече-

E × I

ния, (E.I) – жесткость стержня при изгибе. Действительная работа внутренних сил за счет изгиба от действия момента M бу-

При действии поперечной силы Q касательные напряжения распределены по высоте сечения неравномерно, а следовательно, и сдвиги разных волокон по высоте сечения

55

За счет потенциальной энергии при снятии нагрузки и происходит восстановление размеров и формы разгружаемой системы. При полном снятии нагрузки потенциальная энергия обратится в ноль. Из формулы видно, что потенциальная энергия всегда положительна.

Рассуждая аналогично, запишем выражение возможной (виртуальной) работы внутренних сил:

11.3. Теорема о взаимности удельных перемещений (теорема Максвелла)

Теорема о взаимности перемещений может быть получена как частный случай теоремы о взаимности работ (см. п. 9.1).

Применим теорему о взаимности работ для двух состояний системы при условии, что в обоих состояниях действует лишь по одной единичной силе, приложенной в состоянии (1) в точке “m”, а в состоянии (2) в точке “n” ( см. рисунок).

Применяя теорему о взаимности возможных работ (теорему Бетти), запишем:

Pm × Dmn = Pn × Dnm .

В соответствии с принципом пропорциональности будем иметь:

Dmn = Pn ×δ mn , Dnm = Pm ×δ nm ,

где: δ mn - удельное перемещение точки при-

ложения силы Pm по ее направлению от действия силы Pn = 1 ;

δ nm - удельное перемещение точки при-

ложения силы Pn по ее направлению от действия силы Pm = 1.

Тогда: Pm × Pn ×δ mn = Pn × Pm ×δ nm , или сокращая, окончательно получим:

δ mn = δ nm .

Таким образом: удельное перемещение точки приложения первой единичной силы по ее направлению, возникающее при действии второй единичной силы, равно удельному перемещению точки приложения второй единичной силы по ее направлению, вызванному первой единичной силой.

11.4 Общая формула для определения перемещения от внешней нагрузки

(метод Мора-Максвелла)

Формула Мора-Максвелла, как и теоремы о взаимности возможных работ и о взаимности удельных перемещений, выведена в предположении, что сооружения состоят из идеально упругих и линейно деформируемых тел.

57

Для определения перемещения любой точки системы при действии заданных сил рассмотрим два состояния системы: первое – действительное состояние (a) при действии заданных сил; второе – вспомогательное состояние (b) при действии единичной силы, приложенной в исследуемой точке по заданному направлению (см. рисунок).

Обозначая перемещение точки k при действии сил состояния (a) через Dka и применяя к со-

стояниям (a) и (b) теорему о взаимности возможных работ, получим:

1× Dka = Aab ,

где Aab - работа внешних сил состояния (a)

на перемещениях состояния (b).

Принимая во внимание, что для деформируемых систем в соответствии с принципом воз-

можных перемещений суммарная возможная

работа внешних и внутренних сил на малых возможных перемещениях равна нулю запи-

шем: Aab = - Wab , откуда : Dka = - Wab . Тогда, на основании формулы (в) – см. п. 9.2. получим:

Полученная формула является для определения перемещений в стержневых системах от нагрузки. Заметим, что единичное воздействие прикладывается к системе в том направлении, в котором определяется перемещение. Если после вычислений получим результат со знаком минус, то это значит, что предположение о направлении перемещения оказалось ошибочным. Истинное перемещение в этом случае происходит в сторону, противоположную действию единичной силы.

Таким образом, для определения линейных перемещений во втором состоянии надо в точке, для которой ищется перемещение, приложить силу, равную единице, в направлении искомого перемещения. Если необходимо определить угол поворота сечения, то во втором состоянии прикладывается момент, равный единице.

Полученная в п. 9.4 формула Мора-Максвелла в частных случаях принимает более простой вид, а именно:

А) при расчете ферм, где имеют место лишь осевые усилия N:

58

__

где l – длина стержня фермы, а суммирование выполняется по всем стержням сис-

темы.

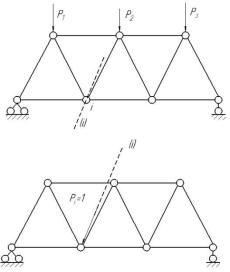
Например, пусть требуется определить перемещение узла i по направлению i от действующей на ферму нагрузки. Для этого:

-определяем усилия во всех стержнях фермы от действующей на нее нагрузки – усилия Np ;

-прикладываем в узел i по направлению i силу P = 1 и определяем от этой силы усилия во

___

всех стержнях фермы – усилия N i ;

- вычисляем для каждого стержня фермы про-

всем “m” стержням получаем искомое пере-

Б) при расчете рам влияние продольных и поперечных сил незначительно и ими можно пренебречь; в этом случае:

При этом, если жесткость EI каждого элемента системы постоянна, то ее можно вынести за знак интеграла

Например, пусть требуется определить перемещение точки i по направлению i от действующей нагрузки. С этой целью:

59

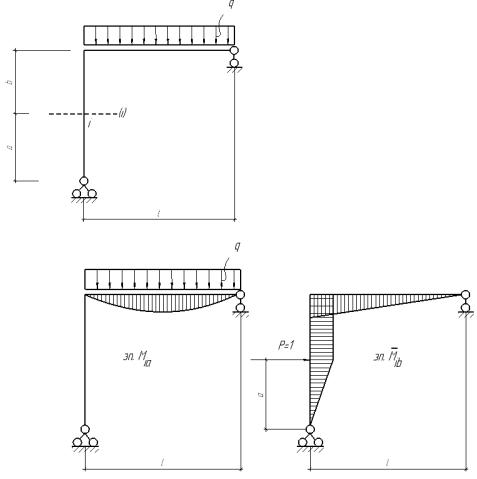
- строим эпюру изгибающих моментов в раме от заданной нагрузки; - строим эпюру изгибающих момен-

тов в заданной системе от единичной силы Pi = 1, приложенной в той точке, перемещение которой определяем и в том направлении, в котором определяем перемещение;

получим искомое перемещение.

11.5. Определение перемещений под действием изменения температуры

Перемещение, вызванное изменением температуры, можно получить на основании

выведенной для случая действия внешних сил, если принять за состояние (a) состояние, соответствующее действию изменения температуры. С этой целью в формуле необходимо сделать следующие преобразования: в первом члене заменить деформацию при удлинении

том сечения dϕi , вызванным изменением температуры; исключить третий член уравне-

60

ния, поскольку при удлинении волокон, вызванном изменением температуры, не имеет

___

места сдвиг и, следовательно, поперечные силы Qb не совершают работы.

Таким образом, под действием изменения температуры, формула для перемещения примет вид:

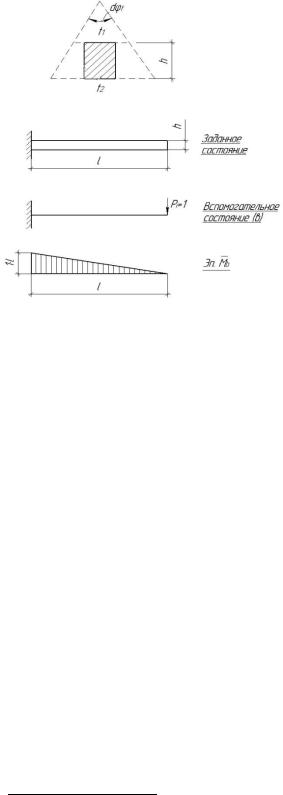
Рассмотрим случай неравномерного нагрева, когда внизу элемент нагрет на t1 градусов, а вверху на t2 градусов, и примем изменение температуры по высоте сечения элемента по прямой. Обозначая коэффициент линейного расширения через α , получим:

-удлинение нижнего волокна . . . . . . . α × t2 × dS ;

-удлинение верхнего волокна . . . . . . . α × t1 × dS

Dkt = (∑α ×tO × WN ). Аналогично, при обратно симметричном изменении температур-

61

11.6. Определение перемещений, вызываемых осадкой опор

Рассмотрим решение этой задачи на примере рамы при перемещении опорного стержня А на величину C. Определим перемещение DiC произвольной точки k по задан-

ному направлению i – i .

Рассмотрим два состояния рамы: за состояние

(a) примем заданное состояние рамы, за состояние (b) – состояние под действием силы P=1, приложенной в точке k по направлению i-i. Составим уравнение работы сил состояния (b), принимая перемещение состояния (a) за возможное.

Обозначая реакцию в опорном стержне A, вызванную силой P=1 через rci . За положительное направление для rci примем то, которое совпадает с положительным направлением перемещения, т.е. по приведенному рисунку rci должна считаться положительной. Принимая заданное перемещение за возможное, составляем уравнение работ для сил состояния P = 1:

1× DiC + rCi ×C = 0,

откуда DiC = - rCi ×C .

Если одновременно происходит несколько перемещений, то DiC = - ∑ rCi × C .

Согласно этой формуле перемещение DiC численно равно работе реакций rci на перемещениях C , взятой с обратным знаком.

11.7. О вычислении интегралов, входящих в формулу перемещений.

11.8.

Способ Верещагина

Пусть эпюра моментов Ma состояния (a) имеет криволинейное очертание, а эпюра моментов Mb состояния (b) прямолинейна. В этом случае можно применить преобразова-

ние интеграла ∫ M a × M b dx , предложенное А. Н. Верещагиным.

62

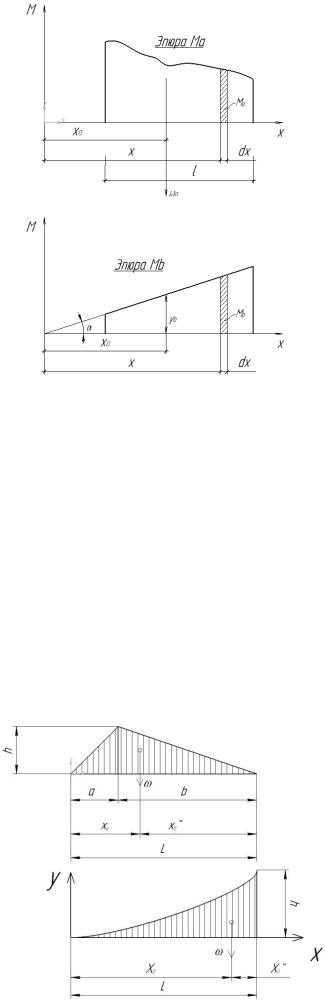
Приняв за начало координат точку пересечения прямой, ограничивающей прямолинейную эпюру Mb с осью абсцисс, получим Mb = x.tg α.

Следовательно:

∫ M a × M b dx = ∫ M a × x ×tgα dx = tgα ∫ x × M a dx.

Как известно, интеграл представ-

ляет собой статический момент S площади эпюры Ma относительно вертикальной оси.

Обозначая площадь эпюры Ma через ωa и абс-

циссу центра тяжести площади эпюры через xo, получим: S = xo ×ωa , следовательно:

tgα ∫ x × M a dx = xo ×ωa ×tgα = yb ×ωa ,

где: yb – ордината эпюры Mb, расположенная под центром тяжести эпюры Ma. Таким образом ∫ M a × M b dx = yb ×ωa (1), т.е. в тех случаях,

когда одна из эпюр моментов прямолинейна, интеграл Мора равен произведению площади криволинейной эпюры моментов на расположенную под ее центром тяжести ординату прямолинейной эпюры.

Этот метод вычисления интеграла называют правилом Верещагина

или перемножения эпюр. Для часто встречающихся в расчетной практике эпюр имеются таблицы, в которых даны значения ∫ M a × M b dx . Направление перемещения, т.е. его знак,

зависит от знаков эпюр. Произведение эпюр (следовательно, и знак перемещения) положительно, если обе эпюры расположены по одну сторону оси стержня, и отрицательно, если эпюры расположены с разных сторон оси стержня (при условии, что обе эпюры построены со стороны растянутого волокна).

Для облегчения пользования формулой (1) полезно запомнить формулы для нахож-

Для параболы, выражаемой уравнением

y = a × xn , участок от x=0 до x= l характери-

зуется величинами:

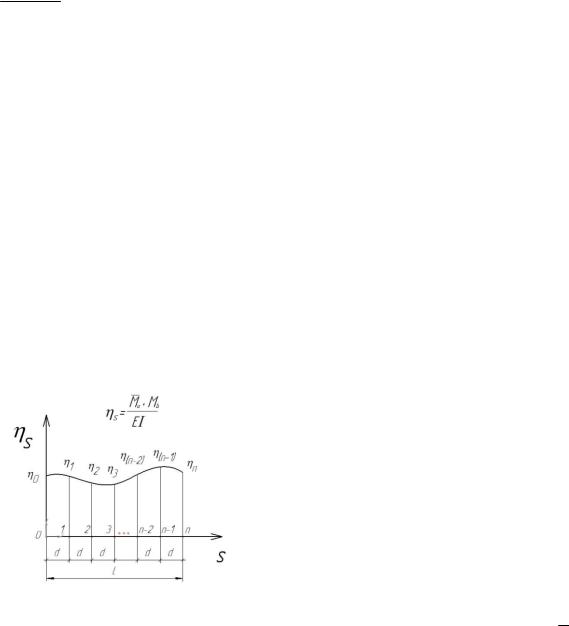
Формула трапеций. Формула Симпсона.

Рассматриваемые формулы удобны для определения перемещений в случае переменного момента инерции сечения и являются формулами приближенного определения интегралов.

Если представляется возможным определить значения подынтегральной функции

__

η = M a × M b в ряде равноудаленных друг от друга сечений, то, полагая, что эта функция

EI

изменяется между смежными сечениями по линейному закону, вычисление такого интеграла с достаточной точностью можно выполнять численно по формуле трапеций:

Вычисление можно уточнить, если считать, что подынтегральная функция η меж-

ду любыми двумя смежными сечениями изменяется по квадратной параболе. В этом случае, при четном количестве участков “n” проводя численное интегрирование по формуле Симпсона, вычисление интеграла примет следующий вид:

+ 2 ×(η2 +η4 + ... +ηn-2 ) +ηn ]

Если длину стержня разделить только на два участка, т.е. принять n = 2 и d = l ,

2

то формула Симпсона будет иметь упрощенный вид:

Задания для самостоятельной работы.

64