8751

130

Если в пространстве есть магнитное поле с индукцией В1 (создаваемое,

например постоянным магнитом), то сила, действующая на кокой – либо проводник с током будет определяться законом Ампера. Если вы поднесете к

проводнику второй магнит, создающий поле В2 , то магнитная сила,

действующая на проводник изменится. Поскольку проводник и ток в нем остались прежними, следовательно изменилось магнитное поле в месте расположения проводника. На опыте можно установить, что сила действия двух

магнитов F1+2 равна векторной сумме сил F1 и F2 , с которыми действует на

элемент тока каждый из магнитов. Используя закон Ампера и свойства аекторного произведения это можно записать в виде:

F1+2 = F1 + F2 = [Il × B1 ] + [Il × B2 ] = [Il × (B1 + B2 )] .

С другой стороны, поскольку сила Ампера определяется вектором магнитной индукции B1+2 , имеющимся в пространстве, можно записать:

= [Il × B1+2 ]. Сравнивая два последних выражения приходим к выводу,

что суммарный вектор магнитной индукции равен векторной сумме индукции магнитных полей, создаваемых каждым магнитом в отсутствии другого:

B1+2 = B1 + B2 .

Сказанное справедливо не только для двух источников магнитных полей, но и для произвольного их числа. Принцип суперпозиции говорит о независимом наложении магнитных полей.

§ 17. Закон Био-Савара-Лапласа

На опыте наблюдается не только взаимодействие между постоянным магнитом и проводником с током, но и между двумя проводниками с током в отсутствие магнита. Можно объяснить наличие силы, действующей на первый проводник тем, что другой проводник с током окружен своим собственным магнитным полем, которое действует на первый проводник по закону Ампера. Таким образом можно сделать вывод, что вокруг всякого проводника с током образуется магнитное поле. Определить индукцию магнитного поля проводника с током можно при помощи закона Био – Савара – Лапласа, являющегося обобщением опытных фактов.

Удобно сформулировать закон генерации магнитного поля для бесконечно малого элемента тока (длиной dl). Тогда, в соответствие с принципом суперпозиции, индукция любого проводника с током может быть найдена в любой точке наблюдения как векторная сумма полей, создаваемых всеми элементами тока, из которых состоит проводник.

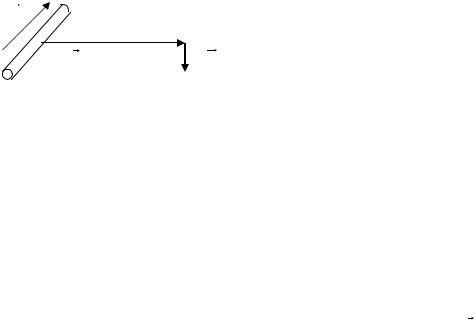
На рисунке изображен элемент тока. Вектор r соединяет элемент тока и точку наблюдения. Индукцию магнитного поля, создаваемую бесконечно малым элементом тока в точке наблюдения обозначим как dB .

131

I

dl

S

dB – элементарное магнитное поле, создаваемое элементарным отрезком провода с током I.

Закон Био – Савара – Лапласа в векторной форме можно записать в виде (используется система Си):

В данной форме закон определяет и величину и направление магнитного поля. Видим, что магнитное поле пропорционально величине элемента тока и

направлено перпендикулярно и элементу тока и вектору r . Здесь μ0 -

магнитная постоянная, равная 4p ×10−7 Тл×м/А. Величина μ учитывает влияние среды, в которой возникает магнитное и называется относительной магнитной проницаемостью. μ показывает во сколько раз в данной среде

индукция магнитного поля больше, чем было бы при тех же условиях в вакууме.

магнитное поле убывает обратно пропорционально квадрату расстояния до точки наблюдения и существенно зависит от направления на точку наблюдения. В частности, электрический ток не создает магнитного поля в точках, лежащих на прямой, совпадающей с направлением тока (a=0).

Кроме индукции для описания магнитного поля используют

напряженность магнитного поля H, в изотропной среде связанную с индукцией по формуле:

B = mm0 H .

На напряженность магнитного поля не оказывает влияния окружающая среда. Она определяется только макроскопическими токами.

Магнитное поле в центре кругового витка с током

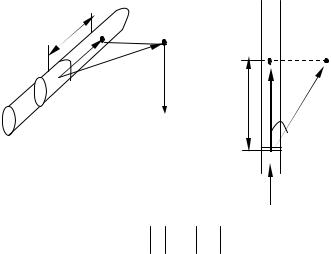
Применим закон Био – Савара – Лапласа для расчета магнитного поля в центре кругового тока. Дано: радиус витка равен R, ток в нем – I .

132

Разделим виток на большое число N кусков. При очень большом числе N каждый элемент тока практически совпадает с направлением касательной к окружности. Проведем из каждого элемента тока, с номером i радиус вектор ri в точку наблюдения (в центр окружности). Очевидно, что все радиусы

перпендикулярны направлению тока в соответствующем элементе (αi = π / 2).

Нетрудно убедиться, что все элементы тока создают одинаково направленное магнитное поле в центре витка – перпендикулярное плоскости витка. В этом случае модуль результирующего магнитного поля можно найти как сумму модулей полей, создаваемых каждым витком:

первых, что расстояния от всех элементов тока до точки наблюдения равны радиусу кольца и, во-вторых, что сумма длин всех элементов тока, на которые мы разбили кольцо равна длине окружности. При выводе этой формулы мы избегали интегрирования. Однако в других случаях расчета полей с использованием закона Био – Савара – Лапласа, интегрирование является необходимым математическим аппаратом.

Магнитное поле прямого тока

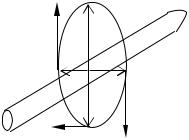
Воспользуемся законом Био – Савара – Лапласа для вычисления магнитного поля, созданного прямым проводом с током. Пусть точка наблюдения удалена от провода на расстояние R. Основные величины, входящие в закон представлены на рисунке (Т.Н. – точка наблюдения):

I

Поскольку все векторы dB параллельны, то модуль вектора суммарной индукции будет равен B = ∫ dB . Для разных элементов тока будет разным

угол a, который удобно выбрать в качестве переменной интегрирования, а расстояния от элементов тока до точки наблюдения выразить через переменную интегрирования.

133

Дифференцируем по переменной a:

Подставляем все в формулу для B и замечаем, что для бесконечного провода угол a может принимать значения от − π / 2 до + π / 2 :

Интересно, что при равенстве токов, магнитное поле на расстоянии R от бесконечного провода с током в π раз меньше, чем в центре витка такого же радиуса. Это связано с тем, что вклад в полное магнитное поле удаленных элементов тока провода быстро убывает с расстоянием до точки наблюдения, а у витка все элементы вносят одинаковый вклад.

§ 18. Линии индукции магнитного поля. Циркуляция

Для наглядного графического изображения магнитного поля так же, как в случае электрического поля, используют линии индукции магнитного поля.

Линия индукции магнитного поля (силовая линия) это линия, касательная в

которой в данной точке совпадает с направлением вектора В.

Найдем направление вектора индукции магнитного поля прямого провода с током в разных точках пространства.

B B

R

Вектор индукции во всех точках окружности радиуса R одинаков по величине и направлен по касательной. Следовательно, линия индукции прямого провода с током есть окружность с центром на оси провода.

Принимая во внимание закон Био – Савара – Лапласа, можно сделать вывод, что линии индукции магнитного поля всегда замкнуты. Так обстоит дело с силовыми линиями элемента тока, которые вблизи от элемента похожи на

134

линии бесконечного прямого тока. Для проводника произвольной формы такая форма линий сохраняется вблизи от провода, где наибольший вклад в поле дает ближайший к точке наблюдения элемент тока.

Замкнутый характер силовых линий магнитного поля принципиально отличает их от аналогичных линий электростатического поля. Это проявляется

при вычислении циркуляции поля. Циркуляцией СВ вектораВ по замкнутому

контуру L называется интеграл:

CB = ∫ B × dL .

L

перемещению единичного заряда по замкнутому контуру L. Ясно, что поскольку электростатическое поле потенциально, CЕ ≡ 0.

В том случае, если циркуляция равна нулю поле называют безвихревым или потенциальным. Если циркуляция отлична от нуля, поле имеет вихревой характер. Таким образом можно сказать, что электростатическое поле – безвихревое.

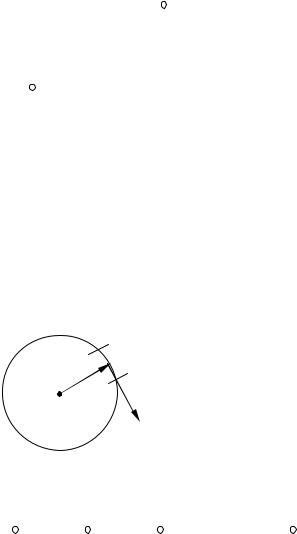
Вычислим циркуляцию магнитного поля прямого провода с током, равным I. В качестве контура L выберем одну линию индукции магнитного поля (окружность радиуса R, изображенную на последнем рисунке).

dl

R

B

Т.к. вектора коллинеарны, то B × dL = B × dL . Тогда

Таким образом мы получили, что циркуляция магнитного прямого провода с током по замкнутому контуру пропорциональна току.

Замечание: Мы убедились, что COB = μµ0I в одном частном случае, однако можно убедиться, что этот закон справедлив всегда. Только справа должен стоять суммарный ток, пронизывающий площадь S(L) , ограниченную контуром L .

S (L)

Закон (теорема) о циркуляции магнитного поля: циркуляция магнитного поля по замкнутому контуру пропорциональна величине суммарного тока,

пронизывающего поверхность, ограниченную этим контуром.

Iсум – сумма токов, которые пронизывают поверхность S (L), ограниченную контуром L.

Используя плотность тока j этот закон можно записать так:

Это соотношение может быть использовано вместо закона Био – Савара – Лапласа для расчета магнитного поля по заданному распределению токов. Если к токам проводимости добавить токи смещения, имеющие место при переменных во времени электрических полях, то полученное соотношение будет представлять собой одно из системы уравнений Максвелла, позволяющей рассчитывать электромагнитные поля во всех ситуациях.

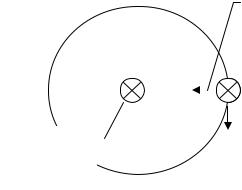
Воспользуемся законом о циркуляции для вычисления индукции магнитного поля внутри длинного соленоида – цилиндрической катушки, на

поверхности которой намотан провод (в изоляции), по которому пропущен ток. В случае длинного соленоида можно пренебречь влиянием его торцов. Магнитное поле соленоида представляет собой сумму полей всех его витков и поэтому направлено вдоль оси.

следовательно, их скалярное произведение равно 0. Окончательно: COB = BL12 . Далее в соответствии с законом о циркуляции, находим суммарный ток, пронизывающий площадку S(L), ограниченную контуром интегрирования. Замечаем, что каждый виток соленоида, расположенный на отрезке L12

136

пронизывает этот контур. Таких витков будет N штук, следовательно суммарный ток в N раз больше, чем I, т.е.

Магнитное поле соленоида определяется произведением тока на число витков, т.е. числом ампер-витков. Удобно использовать также количество

магнитного поля длинного соленоида получим :

B = μμ0 nI -

Реальные соленоиды имеют конечную длину, поэтому данная формула справедлива вблизи центральной части соленоида, а при приближении к его концам поле уменьшается. Нетрудно убедиться, что поле в торцевой части соленоида в два раза меньше, чем в центральной части, поскольку витки расположены только с одной стороны от точки наблюдения.

§ 19. Взаимодействие параллельных токов

Пусть имеется два параллельных проводника, длиной L1 и L2 ,

расположенных на расстоянии R друг от друга. Если по проводникам текут токи I1 и I 2 , то проводники взаимодействуют через создаваемое ими магнитное

поле. Сила F12 действующая на первый проводник со стороны второго может быть найдена по закону Ампера: F12 = [L1 I1 ; B2 ], где B2 - магнитное поле второго проводника в точках расположения первого:

I1

В2

137

Это поле перпендикулярно первому проводнику и обуславливает силу притяжения F12 = L1 I1 B2 , если токи в проводниках одного направления и силу

отталкивания в случае токов противоположного направления. Объединяя две последние формулы для модуля силы получим выражение:

Аналогично можно вычислить силу F21 действия первого проводника на

второй. Мы предлагаем Вам повторить аналогичные рассуждения в качестве упражнения. Однако симметрия задачи позволяет сразу записать выражение для величины этой силы. Действительно, поскольку проводники полностью равноправны, при замене их местами нужно просто изменить их номера. Таким

При этом сила, действующая на единицу длины проводника одинакова для обоих проводников:

F12 = F21 = μμ0 I1 I 2 .

L1 L2 2πR

Полученная формула в системе единиц СИ положена в основу определения единицы силы тока Ампер (А), которая является основной среди электрических

Поэтому можно сказать, что один Ампер, это сила такого тока, который,

протекая по каждому из двух параллельных длинных проводников, вызывает действие силы 2 ×10−7 Н , на единицу длины проводника.

§ 20. Рамка с током в магнитном поле. Магнитный момент

Предположим имеется прямоугольная рамка из проволоки, которая может вращаться относительно вертикальной оси , лежащей в плоскости рамки, а однородное магнитное поле - горизонтально. Если по рамке пропускать ток I, на проводники рамки будут действовать силы Ампера. Поскольку токи в параллельных сторонах рамки имеют противоположные направления, а длины и магнитные поля одинаковы, ясно что силы действующие на противоположные стороны в сумме дают 0. Следовательно равнодействующая всех сил действующих на рамку равна нулю. Это же справедливо и для рамки

138

произвольной формы. В то же время, как мы сейчас увидим, на рамку с током в магнитном поле действует вращающий момент.

Положение рамки, как и любого витка с током принято характеризовать единичным вектором нормали n к плоскости витка. Если угол между вектором нормали и магнитным полем равен α, то силы действующие на горизонтальные стороны рамки (длиной L1 ) равны = IL1 Bcosα . Эти силы имеют

вертикальные направления и не создают вращающего момента относительно оси рамки. Силы, действующие на вертикальные стороны рамки (длиной L2 )

равны FГОР = IL2 × B . Плечо каждой из этих сил относительно вертикальной оси равно d = (L1/2)sinα . Поэтому суммарный вращающий момент сил, действующих на рамку в магнитном поле равен:

M = 2FГОР × d = IL1 L2 Bsinα .

Как видим, существуют два положения, при которых вращающий момент обращается в ноль, когда нормаль рамки направлена вдоль или противоположна магнитному полю (α = 0, π ) . Это положения равновесия

рамки. Одно из этих положения является неустойчивым, а второе устойчивым. Таким образом можно заключить что рамка с током, помещенная в однородное магнитное поле будет поворачиваться пока не займет устойчивого положения равновесия, в котором плоскость рамки перпендикулярна полю. Так же ведет себя в магнитном поле стрелка компаса.

Описанное явление вращения рамки с током в магнитном поле находит практическое применение в электродвигателях и в измерительных приборах.

Аналогичным свойством вращения в магнитном поле обладают витки с током независимо от их формы. Ниже мы приведем без вывода общие формулы для вращающего момента, справедливые для любых витков.

Вектором магнитного момента называют произведение силу тока в витке на площадь витка и на единичный вектор нормали к витку: pm = ISn ,причем из

двух возможных направлений нормали нужно взять то, при котором из конца вектораn ток в витке виден текущим против часовой стрелки. Из сказанного ясно, что вектор магнитного момента витка направлен по нормали к витку.

Величина магнитного момента рамки с током, рассмотренной выше, равна

pm = IL1 L2 .

Используя понятие магнитного момента, выражение для вращающего момента, действующего на виток с током в однородном магнитном поле удобно записать в следующем виде:

= R

M [ pm ; B] .

Эта формула определяет и величину момента и ось вращения витка в магнитном поле. В частном случае прямоугольной рамки с током эта формула соответствует величине момента сил, полученной в начале параграфа, а направление момента показано на рисунке.

139

§ 21. Сила Лоренца. Движение заряженных частиц в магнитном поле

При движении заряженных частиц в магнитном поле на них действует сила, называемая силой Лоренца FЛ , направленная перпендикулярно скорости частицы V и индукции магнитного поля B :

FЛ = q ×[V ; B], q- заряд частицы.

Величину силы Лоренца можно вычислить по формуле модуля векторного произведения: FЛ = q ×VB × sinα , где a - угол между направлением скорости и

индукции магнитного поля. На рисунке показано расположение указанных векторов в случае положительного заряда.

Поскольку движение заряженной частицы в магнитном поле эквивалентно току, ясно что направление силы Лоренца можно определять, как и силы Ампера, по правилу левой руки. Следует при этом иметь в виду, что за направление тока принимается движение положительного заряда. Закон Ампера может быть получен из выражения для силы Лоренца, если просуммировать все силы, действующие на движущиеся в проводнике носители заряда при протекании по нему тока. Поэтому можно сказать, что проявление силы Лоренца является более фундаментальным научным фактом.

Наличие силы, действующей на заряженные частицы в магнитном поле, существенно определяет характер их движения. Очень важным является то, что сила перпендикулярна скорости. Как известно из механики такая сила не совершает работы, следовательно сохраняется кинетическая энергия, а следовательно и модуль скорости частицы. Рассмотрим три возможных случая.

1. Если частица движется вдоль силовых линий магнитного поля (α = 0; или π ), то сила Лоренца обращается в нуль и частица

движется равномерно и прямолинейно.

2. Если частица влетает в магнитное поле перпендикулярно силовым линиям (α = π / 2 ), то она движется с ускорением FЛ /m,

перпендикулярным скорости и магнитному полю, с постоянной по величине скоростью. Такое движение представляет собой равномерное вращение по окружности вокруг силовой линии магнитного поля. Получим выражение для радиуса окружности. Если скорость равна V ,

то сила Лоренца имеет величину qV B и II закон Ньютона для

движения по окружности дает выражение: m × V 2 = qV B , из которого

RЛ

и получим выражение для, радиуса и периода вращения T: