
8445
.pdf
60
p = |
F |
= |
P |
= |
1 |
nm υ 2 . |
|
Dt × DS |
|
||||
|
DS |
3 |
0 |
|||
|
|
|
|
|
|
|
Таким образом, мы получили формулу:
|
|
|
p = |
1 |
|
nm υ 2 . |
(11) |
|
|
|
|
|
|||||
|
|
|
3 |
0 |
|
|||
|
|
|
|
|
|
|
||
Используя понятие средней кинетической энергии теплового движения |
||||||||
молекул ε = |
1 |
m υ 2 |
, уравнение (11) можно записать в виде: |
|
||||
|
|
|||||||
2 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
p = |
2 |
nε . |
(12) |
||
|
|
|
|
|||||
|
|
|
|
|
3 |
|
|
|
Это есть |
основное уравнение молекулярно-кинетической |
теории |
||||||
идеального газа,} которое означает:
давление в газе пропорционально средней энергии теплового движения молекул и числу молекул в единице объема.
1.6.Замечание о средней квадратичной скорости. Распределение Максвелла молекул по скоростям
Выше мы говорили о средней энергии теплового движения молекул. Дело в том, что молекулы движутся неупорядоченно, т.е. их скорости имеют не только случайные направления, но и величину. Спрашивается: какой смысл имеет величина υ2, если разные молекулы имеют разные значения скорости?
Если газ содержит N молекул и занимает объем V, то концентрация молекул равна n=N/V. Предположим, что N1 молекул имеют величину скорости, равную υ1, N2 молекул - скорость υ2 …N k молекул - значение скорости υk. Естественно, что N1 + N2 + … +Nk =N. В таком случае число молекул первой
группы N1', достигающих площадки |
S за время t, будет равно: |
|
|
|||||||
N ¢ = |
1 |
|
N1 |
υ |
DSDt . |
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
6 V |
1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|||
Та же величина для молекул второй группы будет N ¢ |
= |
1 |
N υ |
DSDt / 6 , и так |
||||||
|
||||||||||
|
|
|
|
|
2 |
6 |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
||
далее до молекул k-й группы, из которых достигнет площадки за время
DtN k¢ = 1 N kυk DSDt / 6 . Изменение импульса молекулы каждой группы также будет
6
различным: 2 m0υ1, 2 m0υ2, …, 2 m 0υк. Поэтому суммарное изменение импульса следует записать в виде суммы:
DP = DP + DP + ... + DP = 2m |
(υ |
N ¢ +υ |
|
N |
¢ |
+ ... +υ |
|
N ¢ ) = |
1 |
|
m0 |
(N υ 2 |
+ N υ 2 |
+ ... + N |
υ |
2 )Dt , |
|||||||||
2 |
k |
|
|
|
|
|
|||||||||||||||||||
1 |
2 |
k |
0 |
1 |
1 |
|
|
2 |
|
k |
3 |
|
V |
|
|
1 1 |
2 2 |
k |
|
k |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
то есть вместо формулы (11) получим выражение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
p = |
1 |
|
m0 |
[N υ |
2 |
+ N υ |
2 |
+ ... + N |
υ |
|
2 |
]. |
|
|
|
|
||||||
|
|
|
|
|
|
|
k |
|
|
|
|
||||||||||||||
|
|
|
|
3 |
|
V |
1 1 |
|
2 2 |
|
|
|
k |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||

61
Учитывая, что n=N/V и сравнивая полученное выражение с формулой (11), придем к выводу, что под υ2 следует понимать сумму:
|
N υ 2 |
+ N υ 2 |
+ ... + N |
υ |
2 |
|
N |
1 |
|
2 |
|
N |
2 |
|
2 |
|
N |
k |
2 |
|
|
|
(υкв ) 2 = |
1 |
1 |
2 2 |
k |
k |
|
= |
|
υ1 |
|
+ |
|
υ2 |
|
+ ... + |
|
υk |
. |
(13) |
|||
|
|
N |
|
|
|
N |
|
N |
|
N |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Таким образом, |
при упрощенном выводе формулы (11) |
мы заменили |
||||||||||||||||||||
реальные скорости частиц некоторой средней скоростью, которая согласно только что полученной формуле является средней квадратичной скоростью, квадрат которой равен среднему арифметическому квадратов скоростей всех молекул газа. В частности, если имеется только 2 молекулы, движущиеся со скоростями υ1 и υ2 (k=2, N1=N2=1, N=2), υ2=(υ21+υ22)/2.
Средняя энергия теплового движения молекул равна кинетической энергии молекулы, движущейся со средней квадратичной скоростью.
В действительности молекулы могут иметь не дискретные, а непрерывные значения скоростей. Следовательно, в реальности число групп k молекул, имеющих разные скорости, бесконечно велико k→∞. В этом случае относительные доли числа молекул N1/N, N2/N, …, имеющих соответствующие скорости, следует заменить аналогичной величиной dF(υ):
υ = dN (υ) dF ( ) ,
N
которая равна числу молекул, имеющих величину модуля скорости большую υ-dυ, и меньшую υ+dυ, деленную на полное число частиц. Понятно, что чем больше величина dυ, тем больше dF(υ): dF(υ)=f(υ) dυ, где f(υ) - функция, характеризующая распределение молекул по величине скорости.
Сучетом сказанного формула (13) в этом случае может быть переписана
ввиде (сумма преобразуется в интеграл):
(υкв ) 2 = |
1 |
∫ |
υ 2 × dN (υ) = |
∫ |
υ 2 × dF (υ) = |
∞ υ 2 × f (υ) × dυ , |
(14) |
|
N |
||||||||
|
|
|
∫0 |
|
причем интегрирование проводится по всем возможным значениям модуля скорости.
В случае идеального газа, находящегося в тепловом равновесии, функция f(υ) была получена Дж.. Максвеллом и имеет вид:
|
μ |
|
3 / 2 |
|
|
μυ 2 |
|
|
|
|
|
|
|
|
|
2 |
|
||
f (υ) = 4π |
|
|
|
- |
×υ |
|
, |
||
|
|
exp |
|
|
|||||
|
2πRT |
|
|
|
2RT |
|
|
|
|
где μ - молярная масса газа, а T - равновесная температура. Таким образом, величина (υкв)2 для одноатомного идеального газа определится значением интеграла2
|
|
|
|
|
μ |
|
3 / 2 |
∞ |
|
|
|
|
μυ 2 |
|
3RT |
|
(υ |
кв ) |
2 |
= 4π |
|
|
∫0 |
υ |
4 |
|
- |
|
× dυ = |
|
. |
||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
× exp |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
μ |
|
||||
|
|
|
|
|
2πRT |
|
|
|
|
|
|
2RT |
|
|
||
2 при вычислении интеграл можно преобразовать к интегралу Пуассона
∫0∞ exp(-aυ 2 ) × dυ = 1/ 2
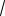 π / a
π / a

62
Таким образом, средняя квадратичная скорость молекул одноатомного газа равна:
υкв = |
3RT |
. |
|
||
|
μ |
|
Далее мы получим этот результат элементарными методами, что показывает справедливость упрощенного подхода, примененного при выводе основного уравнения молекулярно-кинетической теории.
Сопоставление с уравнением Клайперона - Менделеева.
Воспользовавшись тем, что концентрация молекул n=N/V, основное уравнение молекулярно-кинетической теории можно записать в виде:
pV = 2 Nε .
3
Сравнивая это выражение с уравнением состояния идеального газа (10), приходим к выводу, что:
ε= 3 m RT .
2 μ N
Сдругой стороны, число молекул газа можно выразить через число молей
ичисло Авогадро: N=νNа= mμ Nа. Поэтому для средней кинетической энергии
молекул получим формулу:
ε = |
3 |
|
RT |
. |
(15) |
|
|
||||
2 |
|
N a |
|
||
Напомним, что согласно формуле (7), универсальная газовая постоянная R относится к одному молю газа, содержащему Nа молекул. Из последнего выражения видно, что удобно ввести новую постоянную k, представляющую собой универсальную газовую постоянную в расчете на одну молекулу:
k = |
R |
= 1,38 |
×10 |
−23 |
Дж |
(16) |
N a |
|
К |
||||
|
|
|
|
|
Фундаментальная постоянная k называется постоянной Больцмана. Теперь формулу (1.16) можно записать в виде:
ε = |
3 |
кТ . |
(17) |
|
|||
2 |
|
|
|
Интересно, что средняя кинетическая энергия молекул газа определяется только температурой газа. Следовательно, если два газа имеют молекулы разной массы, то среднеквадратичная скорость больше у газа с более легкими молекулами.
В заключение данного пункта приведем альтернативную форму уравнения состояния идеального газа, которую можно получить, если в уравнении (10) заменить универсальную газовую постоянную, воспользовавшись выражением (16):
р=nkT. |
(18) |
Такое же соотношение получится, если подставить величину ε из формулы (17) в основное уравнение молекулярно-кинетической теории.

63
1.7.Закон равнораспределения энергии по степеням свободы. Внутренняя энергия идеального газа
Как было показано ранее, средняя кинетическая энергия ε поступательного движения молекулы идеального газа может быть выражена
через среднюю квадратичную скорость υ:
ε = m0υ 2 . 2
С другой стороны, квадрат любого вектора можно представить как сумму
квадратов его координат:
υ2=υ2x+υ2y+υ2z.
Беспорядочность движения по всем направлениям означает, что должно
быть: υ2x=υ2y=υ2z . Следовательно,
υ2x=υ2y=υ2z=υ2/3
С другой стороны, величины m0υ2x/2, m0υ2y/2, m0υ2z/2 представляют собой энергию поступательного движения вдоль каждой из трех осей координат или
энергию, приходящуюся на одну степень свободы.
Числом степеней свободы называется число независимых координат, которые необходимо задать для определения положения тела в пространстве.
Положение материальной точки в пространстве определяется тремя координатами - 3 степени свободы. Для того, чтобы задать положение гантельки (т.е. тела, состоящего из двух жестко связанных материальных точек), необходимо задать положение ее центра масс (три координаты) и еще два угла, которые составляет ось гантельки с двумя из осей координат (угол с третьей осью координат не является независимым) - 5 степеней свободы. В общем случае несимметричное твердое тело имеет 6 степеней свободы.
В случае поступательного движения молекул газа, как мы уяснили, на каждую степень свободы приходится 1/3 общей энергии молекулы, т.е.
ε 0 = 1 kT .
2
Если молекула состоит из двух и более атомов, полное число степеней свободы i увеличивается:
i=iпост+iвр.
При этом в тепловом равновесии на каждую степень свободы по- прежнему будет приходиться энергияε0 . Таким образом, с учетом возможности вращательного движения сложных молекул средняя энергия ε движения одной молекулы равна:
ε = ε |
|
× i = |
i |
kT , |
i=i |
+i |
|
. |
0 |
|
вр |
||||||
|
2 |
|
пост |
|
|
|||
|
|
|
|
|
|
|
||
Из сказанного ясно, что энергия движения двухатомных молекул равна 5kT/2 (iвр=2), а трех и более атомных молекул - 3kT (iвр=3).
64
Внутренняя энергия идеального газа. Как уже говорилось, расстояние между молекулами газа при нормальных условиях примерно в 10 раз больше характерного размера молекул. Это означает, что молекулы находятся далеко друг от друга и силой взаимодействия между ними, а следовательно энергией их взаимодействия, можно пренебречь. Именно такая модель невзаимодействующих молекул соответствует идеальному газу.
Внутренняя энергия идеального газа представляет собой суммарную
кинетическую энергию всех молекул данной массы газа.
Средняя кинетическая энергия одной молекулы равна <ε0>=ikT/2, где i - число степеней свободы:
i=3 - для газов, молекулы которых состоят из одного атома и не имеют вращательных степеней свободы (это имеет место для всех инертных газов, например He;
i=5 - для O2, N2, H2 и большинства других простых газов, имеющих двухатомные молекулы;
i=6 - для CO2, паров воды H2O) и других газов, имеющих трех-и более атомные молекулы.
Поскольку в одном моле газа содержится Nа молекул, внутренняя энергия одного моля газа равна:
U μ |
= N a ε 0 = iN a |
kT |
= |
iRT |
. |
(19) |
2 |
|
|||||
|
|
2 |
|
|
||
Если масса газа равна m, это составляет ν=m/μ молей. Следовательно, внутреняя энергия Um массы m газа определится формулой:
U m |
= νU μ = |
m |
× |
iRT |
. |
(20) |
|
|
|||||
|
|
μ 2 |
|
|||
Важно! Внутренняя энергия идеального газа зависит только от температуры и не меняется при изменении объема и давления (если при этом
T=const).
В случае других веществ и реальных газов (сжатые до p=100 атм. и более при комнатной температуре газы) ситуация другая. Поскольку концентрация молекул n=p/(kT) возрастает с ростом давления, то объем V1=1/n, приходящийся на одну молекулу, становится сравнимым с объемом самой молекулы. Молекулы сильно сближаются и становится существенной энергия взаимодействия между ними (потенциальная энергия). В этих условиях внутренняя энергия будет зависеть и от расстояния между молекулами, т.е. от объема газа.
65
2.Термодинамический подход
2.1.Первое начало термодинамики
На основе обобщения многих экспериментальных фактов установлено, что если путем теплообмена с окружающей средой термодинамической системе передано количество теплоты Q и при этом система совершила против внешних сил работу A, то строго выполняется следующее соотношение:
Q=DU + A.
Количество теплоты, полученное системой, расходуется на изменение ее внутренней энергии и на совершение системой работы против внешних сил. Это положение получило название первого начала термодинамики и, по сути, является обобщением закона сохранения энергии на тепловые процессы.
Для бесконечно малого изменения состояния системы первое начало термодинамики имеет вид:
dQ=dU+dA.
Здесь dU является полным дифференциалом, поскольку зависит только от начального и конечного состояния системы. В то же время, количество теплоты dQ и работа dA не являются полными дифференциалами, а зависят от того, каким путем происходило измерение состояния системы, т.е. от конкретного вида процесса. Первое начало термодинамики показывает, что система не может совершить работу, если к системе не подводится теплота или не уменьшается внутренняя энергия системы. Это положение, сформулированное как невозможность создания вечного двигателя первого рода, является одной из альтернативных формулировок первого начала термодинамики.
Итак, обмен энергией между термодинамической системой и другими телами и системами может быть результатом двух качественно различающихся процессов:
·совершения работы системой или над системой;
·передачи или получения системой теплоты (теплообмен).
2.1.1. Работа, производимая термодинамической системой
Понятие физической работы вводилось при изучении раздела <<механика>> (предлагаем вам вновь просмотреть соответствующий материал). В термодинамике состояние системы и работу, совершаемую системой принято выражать через термодинамические параметры. В данном разделе будет получено соответствующее выражение.
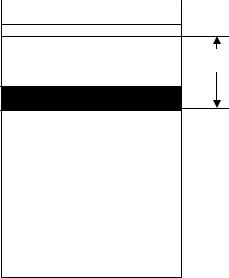
Рассмотрим газ, заключенный в цилиндр с легко скользящим (без трения) поршнем (см. рис. 7). Пусть газ расширился, при этом поршень переместился вверх на величину dx. Элементарная работа газа при расширении равна:
δA=F×dx,
66
где F - сила давления на поршень. Выразим F через давление газа р и площадь поршня s:
F=p×s.
S
DV Dx
p, V
Рис. 7. Схема вычисления работы при расширении газа
Тогда δA=р×s dx, а учитывая, что s d=dV - приращение объема
газа, получим:
δA=p×dV. |
(21) |
Если dV>0 , то и δA >0 и говорят, что работу совершает газ; если dV<0, то δA <0 и в этом случае работа совершается над газом, поскольку в последнем случае будет положительной работа внешних сил (по III закону Ньютона внешние силы равны силам давления газа, но имеют противоположное направление, поэтому их работа отличается знаком от работы газа). В частности, при изохорическом процессе, когда V=const, dV=0, элементарная работа δA =0. Это обстоятельство аналогично механической ситуации, когда при наличии силы тело покоится и, следовательно, не совершает работу.
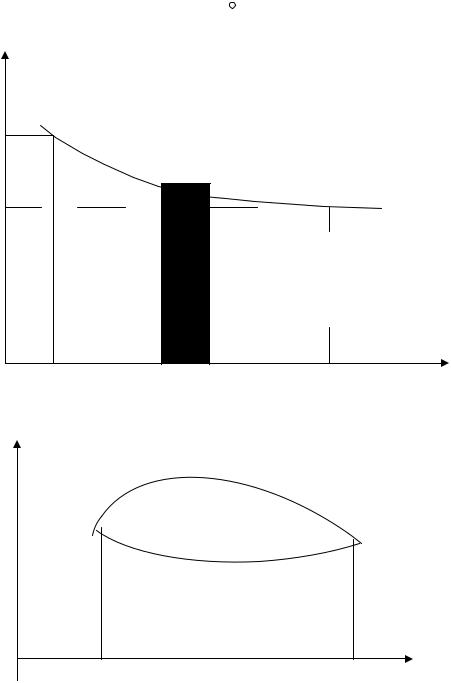
Изобразим процесс изменения объема газа графически в координатах {р,V}. Пусть начальное состояние газа соответствует точке 1 со значениями р1, V1, а конечное состояние - точке 2 со значениями р2, V2. Процесс графически можно представить кривой, соединяющей точки 1 и 2 (кривая а на рис. 8). Элементарная работа δA, определяемая формулой (21), равна площади заштрихованной площадки. Полная работа A1-2 равна сумме всех элементарных работ от точки 1 до точки 2 и может быть найдена путем вычисления интеграла:
2 |
2 |
|
A = ∫ dA = ∫ p × dV |
(22) |
|
1 |
1 |
|
и эквивалентна всей заштрихованной области, лежащей под кривой, изображающей процесс (в нашем случае 1-а-2). В случае обратного процесса 2-
67
а-1 работа изображается той же площадью, но имеет противоположный знак (в этом случае dv отрицательно).
Если бы газ переходил из состояния 1 в состояние 2 по кривой 1-b-2 (см. рис. 9), лежащей ниже кривой 1-a-2, то работа газа была бы меньше. Следовательно, работа, совершаемая газом в процессе перехода из одного состояния в другое, зависит от того, как именно, по какому пути, через какие промежуточные состояния совершился этот переход.
Если газ совершил цикл 1-a-2-b-1, то несмотря на то, что система возвращается в исходное состояние, работа при этом круговом процессе не равна нулю:
2
A = ∫ dA1 ¹ 0 .
p
p1
p
p2
V
V1 |
V |
υ2 |
|
Рис. 8. Работа системы при ходе процесса |
|
p |
a |
|
1 |
2 |
b
V
C D
Рис. 9. Работа кругового процесса

68 |
|
Таким образом, работа, в отличие от внутренней энергии, не |
является |
функцией состояния системы и dA не может рассматриваться как полный дифференциал некоторой функции A. Для того, чтобы подчеркнуть это обстоятельство, в термодинамике элементарную работу изображают dA (в отличие от дифференциала внутренней энергии dU).
2.1.2. Количество теплоты и теплоемкость
Теплота, как и работа, не является функцией состояния, а зависит от процесса изменения состояния системы. Поэтому элементарное количество теплоты тоже обозначается частным дифференциалом dQ. В системе СИ теплота, как и другие виды энергии, измеряется в джоулях (Дж). На практике широкое распространение имеет и другая единица теплоты - калория (кал). Калория - это количество теплоты, необходимое для нагревания одного грамма воды на один градус. Одна калория составляет 4,18 джоуля:
1кал=4,18 Дж.
Спонятием теплоты тесно связано понятие теплоемкости. Теплоемкостью тела называется величина, равная количеству теплоты, которое надо сообщить телу, чтобы повысить его температуру на один градус. Если к телу
подведено некоторое количество теплоты dQ, в результате чего температура его увеличилась на dT, теплоемкость тела Cтела равна:
Стела |
= δQ . |
(23) |
|
dT |
|
В СИ теплоемкость тела измеряется Дж/К.
Если тело однородно, то используются понятия удельной теплоемкости c и молярной теплоемкости C.
Удельной теплоемкостью c называется теплоемкость единицы массы вещества. Значит, если масса тела равна m, то удельная теплоемкость равна
c=Cтела/m. В СИ c измеряется в Дж/(кг×К).
Молярной теплоемкостью С называется теплоемкость одного моля вещества. Она измеряется в Дж/(моль К). Поскольку моль содержит массу вещества, равную молярному весу m, можно написать связь молярной и удельной теплоемкостей:
С=m×с |
(24) |
Удобство введения понятий удельной и молярной теплоемкостей объясняется тем, что эти величины не зависят от массы тел, а определяются лишь свойством материала3, что облегчает составление таблиц. Если известна молярная или удельная теплоемкости процесса, элементарное количество теплоты можно подсчитать по формулам:
δQ = m × c × dT , или δQ = |
m |
× C × dT . |
(25) |
|
|||
|
μ |
|
|
3 Иногда теплоемкость существенно зависит также от характера процесса, сопровождающего теплообмен. Например, в случае газа различают теплоемкости процессов при постоянном давлении и постоянном объеме. Эти вопросы мы скоро подробно обсудим.}
69
2.1.3. Применение первого начала термодинамики к
изопроцессам в идеальном газе
Для равновесных процессов, протекающих в газах, элементарная работа,
производимая газом против внешних сил, состоит в работе расширения (21),
поэтому первое начало термодинамики может быть записано в виде:
dQ=dU+p×dV (26)
Изохорный процесс (V=const). В этом случае, как уже отмечалось, работа, совершаемая газом против внешней силы, равна нулю. Первое начало
термодинамики для изохорного процесса примет вид: |
|
dQ=dU |
(26а) |
Таким образом, в изохорном процессе вся теплота, подведенная к газу, идет на увеличение его внутренней энергии. Используя уравнение (25), выразим изменение теплоты dQ через изменение температуры dT
|
|
δQ = |
m |
× C × dT , |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
μ |
υ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где Сυ - молярная теплоемкость газа при постоянном объеме. |
Согласно (26) |
||||||||
приращение внутренней энергии при этом процессе примет вид: |
|
||||||||
dU = |
m |
× C × dT , или |
dU |
= |
m |
× C . |
(27) |
||
|
|
|
|||||||
|
μ |
υ |
|
|
dT |
|
μ |
υ |
|
|
|
|
|
|
|
|
|||
С другой стороны ранее было получено выражение для внутренней энергии идеального газа в зависимости от числа i степеней свободы составляющих его молекул: U=i mRT/(2μ). Продифференцировав это соотношение по T, получим формулу:
|
dU |
|
im |
|
||||
|
|
= |
|
|
|
R , |
(28) |
|
|
dT |
2μ |
||||||
сравнивая которую с (28), получим выражение для Cυ: |
|
|||||||
|
С |
= |
iR |
|
(29) |
|||
|
|
|||||||
|
|
υ |
2 |
|
|
|||
|
|
|
|
|
||||
Таким образом, молярная теплоемкость при постоянном давлении для идеального газа не зависит от термодинамических параметров, а определяется характером газа (числом степеней свободы молекул).
Изобарный процесс (p=const). Примером изобарного процесса может служить процесс теплообмена с газом, находящимся в цилиндре под поршнем (рис.7), нагруженным постоянной внешней силой. В соответствии с (22) работа, совершаемая газом против внешней силы, равна:
Ар=р×(V2-V1) |
(30) |
и может быть найдена как площадь фигуры под линией изобары, которая в координатах (p,V) имеет вид прямоугольника. Уравнение первого начала
